Folytatva az elmúlt hetekben megkezdett sorozatot, végre szeretnék rákanyarodni a lényegre; mármint, hogy miről is szól Bayes tétele. Az előző két bejegyzésben (Folt a zsákját – Thomas Bayes kísérlete és Üstökös Franciaország egén) nagyjából összefoglaltam a tétel születésének történetét, akkor most térjünk rá arra, hogy mire jó és hogyan alkalmazható a gyakorlatban.
Bayes tételének mai formáját 1810 és 1814 között dolgozta ki:
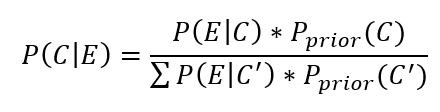
Jó, de mit jelent megint ez a bonyolult képlet a valóságban? A képletben szereplő E jelenti az eseményt (angolul event), a C pedig az okot (angolul cause). Más forrásokban az okot (cause) feltevésként (hypothesis), az eseményt (event) pedig bizonyítékként (evidence) is szokták említeni. Bizonyos esetekben ez az alternatív elnevezés használthatóbb, mint az első, de ezt majd később látni fogjuk.
Néhány példa eseményre (bizonyíték) vagy okra (feltételezés):
- Esemény lehet például, hogy valaki tüdőrákot kap, ennek oka pedig lehet az, ha az illető dohányzik
- Esemény lehet, hogy egy hölgy terhességi tesztje pozitív, ennek oka pedig az, hogy a hölgy valóban áldott állapotban van
- Esemény lehet egy szó vagy szókapcsolat megjelenése egy e-mailben, ennek oka pedig az, hogy az üzenet spam.
Másképpen fogalmazva
- A feltevés az, hogy az illető dohányzik, ennek bizonyítéka pedig az, hogy az illető tüdőrákos lett
- A feltevés az, hogy egy hölgy áldott állapotban van, ennek bizonyítéka pedig az, hogy a terhességi tesztje pozitív
- A feltevés az, hogy az üzenet spam, ennek bizonyítéka pedig az, hogy bizonyos szavak vagy szókapcsolatok szerepelnek az üzenet szövegében.
A tört nevezőjében szereplő C' viszont az okra vonatkozó teljes valószínűséget jelenti, vagyis, annak a valószínűségét, ha
- az esemény az, ha valaki tüdőrákot kap, de azt is figyelembe véve, ha dohányzik és azt is, ha nem
- Az esemény lehet az, hogy a terhességi teszt pozitív, de akkor is, ha a hölgy valóban terhes és akkor is, ha nem
- Az esemény az, hogy a szövegben előfordulnak bizonyos szavak vagy szókapcsolatok, de beleértve azt is, hogy az üzenet spam és azt is, ha nem.
A képlet alkalmazásának nehézségét nyilvánvalóan nem a kalkuláció bonyolultsága adja, inkább a képletben szereplő egyes valószínűségek azonosítása jelenti.
Egy korábbi bejegyzésben (Ez bizony függőség! – Még egy kicsit a feltételes valószínűségekről) már tisztáztuk, hogy mit is jelent a két betű közötti függőleges vonal (Ez persze megint felér egy egyiptomi hieroglifával, de egy bizonyos szint felett ezt sajnos nem tudom elkerülni).
A kifejezések magyarázatát kezdjük az egyenlőségjel bal oldalával:
P(C|E) jelenti azt a valószínűséget, hogy az ok fennáll, ha az esemény megtörténik. A fenti példáknál maradva ez például lehet a valószínűsége annak, hogy egy üzenet spam, ha szerepel benne egy adott szó vagy kifejezés. Legtöbbször ezt nehéz megmondani, mert mondjuk a spam üzenetek esetében nehéz megállapítani, hogy attól spam-e egy üzenet, mert egy adott szó vagy kifejezés szerepel benne.
P(E|C) annak a valószínűségét jelzi, hogy ez esemény megtörténik, ha az ok fennáll. Ez pedig annak a valószínűsége, hogy ha egy üzenet spam, akkor egy adott szó vagy kifejezés szerepelni fog benne. Ezt a legtöbb esetben könnyű mérni, mert egy üzenetet elolvasva el tudjuk róla dönteni, hogy az spam-e vagy sem, utána pedig meg lehet számolni, hogy ezek hány százalékában van benne az adott kifejezés.
A Pprior(C) az ok valószínűségének előzetes becslése, vagyis az, hogy a beérkező üzenetek hány százaléka spam. Ez az, ami a legtöbb vitát gerjeszti a tudósok között, mert amikor legelőször vizsgáljuk az adott eseményt és okot, akkor sok esetben nincs tényeken alapuló számszerű valószínűség, amelyet figyelembe vehetnénk (lásd Bayes kísérletét a golyókkal az asztalon). A második ismétlésnél már nincs gond, mert akkor már az első kör eredményét fogjuk ide behelyettesíteni.
Számomra a legkevésbé érthető a nevezőben lévő képlet. Ez az összes lehetséges hipotézis valószínűségeinek az összessége, vagyis

Huhh! Ez most megint mit is jelent? A szumma jel ugye összegzést jelent. De mit is adunk össze ez esetben? A fenti képletben az első rész ugye megegyezik a számlálóban lévő szorzattal, vagyis az előző példánál maradva P(E|C) annak valószínűsége, hogy ha egy üzenet spam, akkor az adott kifejezés mekkora valószínűséggel van benne, Pprior(C) pedig annak a valószínűsége, hogy az üzenetek hány százaléka spam.
A kifejezés második részében viszont a C-k előtt van egy-egy ~ jel. Ez a jel azt jelenti, hogy vesszük C ellentettjét. Ha C azt jelenti, hogy az üzenet spam, akkor ~C azt jelenti, hogy az üzenet NEM spam. Ebben az esetben tehát a P(E|~C) annak a valószínűsége, hogy az üzenet tartalmazza a keresett szót, de az üzenet NEM spam! Pprior(~C) pedig annak a valószínűsége, hogy az üzenet NEM spam!
Kedves olvasó! Ha esetleg most ledobtad volna a láncot vagy elérkeztél tűrőképességed határáig, akkor kérlek, pihenj egyet, végezz el néhány ellazító jóga gyakorlatot és próbáld meg kibírni a végéig. A sztori bonyolultnak tűnik, de valójában nem annyira vészes, csak rá kell hangolódni!
Szóval, ha újra elérted az átszellemültségnek azt az optimális szintjét, hogy be tudd fogadni a továbbiakat, akkor folytassuk! Nézzük meg mindezt egy számszerű példán keresztül:
A történet arról szól, hogy az orvosnál egy rutin teszt elvégzésekor kiderül, hogy elkaptál egy ritka, de súlyos betegséget. Ez a betegség olyan ritka, hogy az emberiségnek csak 0,1%-a kapja el azt, vagyis minden 1000 emberből 1. A betegséget kimutató teszt eredményessége 99%, azaz minden 100 tesztből 99 esetben helyes eredményt ad, egyetlen esetben ad fals pozitív eredményt, azaz mutatja egy egészséges emberről azt, hogy beteg.
„Doktor úr! Akkor most meg fogok halni?”
Egy ilyen esetben a legtöbben így reagálnánk. De mégis? Mekkora a valószínűsége annak, hogy tényleg megkaptam ezt a ritka, de végzetes betegséget? Elsőre rávágnánk, hogy persze, 99%.
De vizsgáljuk ezt meg a Bayes-tétel szemszögéből!

Amit keresünk, az a P(C|E) vagyis annak a valószínűsége, hogy ha a teszt eredménye pozitív (E), akkor valóban beteg vagy (C).
P(E|C) annak a valószínűsége, hogy ha valóban beteg vagy, akkor a teszt eredménye pozítív. Ez 99%, vagyis 0,99.
Pprior(C) annak a valószínűsége, hogy valóban elkaptad a betegséget. Mivel 1000 emberből átlagosan 1 kapja el ezt a kórt, a valószínűség 0,1% vagy 0,001. Ez esetben szerencsések vagyunk, mert olyan adat, amelyből ki tudunk indulni, nem kell a hasunkra ütve kitalálni a legelső értéket.
Nézzük a nevezőt:
A P(E|C)*Pprior(C) ugyanaz, mint a számlálóban. P(E|~C)-ről azt mondtuk, hogy annak a valószínűsége, hogy a teszt pozitív lesz annak ellenére, hogy nem vagy beteg. Ennek a valószínűsége 1%, azaz 0,01 hiszen a teszt 100 esetből 1 alkalommal fog fals pozitív eredményt mutatni. Pprior(~C) pedig ugye annak az esélye, hogy nem vagy beteg, ez 99,9% vagy 0,999, hiszen 1000 emberből 999 nem kapja el ezt a betegséget.
Végig vettük az összetevőket, akkor most süssük meg a sütit!

Az eredmény elsőre több, mint meglepő, de talán mégsem. Józan paraszti ésszel végiggondolva ha minden 100 emberből 1-nek a tesztje hibás, akkor mind az ezer embert letesztelve 10 ember tesztje lesz hibás, és abból te csak egy vagy, vagyis hiába nagyon jó a teszt megbízhatósága, mivel a betegség igen ritka, ezért elég kicsi a valószínűsége annak, hogy tényleg beteg vagy, inkább az a valószínű, hogy te vagy a 100 emberből az az 1, akinek fals pozitív lett a tesztje.
A történteket ily módon végig gondolva adja magát a következtetés, hogy kérsz még egy tesztet. Elmégy egy másik klinikára és kéred, hogy végezzék el ők is a tesztet (hogy a két teszt eredménye független legyen egymástól). Ha a második teszt eredménye is pozitív lenne, akkor mekkora lenne a valószínűsége annak, hogy elkaptad a kórt? Nos, ehhez vesszük ugyanazt a képletet, de a Pprior(C) = 0,001 helyére behelyettesítjük az előző teszt által adott valószínűséget, a 9%-ot, azaz 0,09-et, hiszen az előző teszt alapján megtanultuk, hogy 9% az esélye, hogy beteg vagy. Persze ez megváltoztat még két másik értéket is a nevezőben, erre figyelni kell!

Vagyis, ha azokat, akiknek pozitív lett a tesztje, újra letesztelnénk, akkor a teszt magas megbízhatósága miatt a két teszt eredménye már nagy valószínűséggel megmutatja a valóságot.
Arra azért ügyeljünk, hogy az eredmény és a második kör szükségessége a betegség előfordulási valószínűsége és a teszt megbízhatóságának függvényében változhat.
Ez a példa nemcsak azért szimpatikus, mert elég gyakorlatias ahhoz, hogy könnyen el lehessen képzelni, hanem amiatt is, mert bemutatja Bayes tételének iteratív jellegét. Azt, hogy hogyan működik az ciklus, ahogyan az ismétlések során minden egyes újabb információval egyre közelebb jutunk a valós valószínűségekhez. Bár volt egy hosszú időszak, amely során a módszer alkalmazása erősen háttérbe szorult, a 20 század története során igen sok jelentős felfedezés vagy eredmény kötődik a módszer alkalmazásához, amelyből néhányat talán majd én is bemutatok a későbbiekben.





