Az előző bejegyzésben elkezdtem bemutatni egy relatíve egyszerű példán keresztül bemutatni a Bayes-i keresési algoritmus alkalmazását az R és az RStudio statisztikai programcsomag segítségével. Az előző alkalommal ott hagytam abba, hogy sikerült létrehozni egy olyan adatsort, amely a keresési terület mind a 3721 mezőjéhez hozzárendelte annak a valószínűségét, hogy a keresett objektum abban a mezőben található. A következő lépés az, hogy figyelembe vegyük az elveszett objektum detektálásának valószínűségét.
Most azt feltételezzük, hogy van egy valamilyen szonár, szenzor vagy más felderítő eszköz, amelyet a kereséskor alkalmazunk. A felderítő eszköznek szintén van egy bizonytalansága, minél messzebb van a detektált tárgy a detektáló eszköztől, annál kisebb a valószínűsége annak, hogy az eszköz észleli a tárgyat, ha az ott van. Tehát a detektálás esélye a tárgy és a szonár sugárirányú távolságával arányosan csökken. A detektornak ezt a tulajdonságát úgy vesszük figyelembe, hogy ha a detektor az adott mezőben például 97,5%-os valószínűséggel képes detektálni az elveszett objektumot, ha az ott van. Minél távolabb van egy mező a keresés helyszínétől, annál kisebb lesz a detektálás esélye. Ezt a változást a következő összefüggéssel vesszük figyelembe:
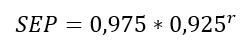
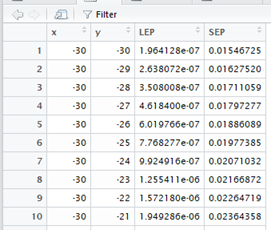
Ahol r a mező sugárirányú távolsága a detektor helyétől. A SEP kifejezés a Search Effectiveness Probability angol rövidítése, amely azt adja meg, hogy ha a keresett objektum egy adott mezőben van, akkor mekkora annak a valószínűsége, hogy a detektor megtalálja. Nos, tegyük fel, hogy a detektor az x = 10 és y = 5 mezőben van, jelöljük ezt a továbbiakban így: [10; 5]. A következő feladat az, hogy mind a 3721 mezőre kiszámoljuk ezt a SEP értéket. A számítás elvégzéséhez először is írnunk kell egy saját függvényt, nevezzük ezt detectionpower()-nek.
detectionPower <- function(x, y, dx = 10, dy = 5, p0 = 0.975, d = 0.925) {
x2 <- x – dx
y2 <- y – dy
r <- sqrt(x2^2 + y2^2)
detectionpower <- p0 * d^r
}
A függvény tulajdonképpen nem tesz mást, minthogy kiszámolja a paraméterként megadott x és y koordinátájú mező sugárirányú távolságát a [10; 5] mezőtől, ahol a detektor található, majd a fent említett képlettel kiszámítja a hozzá tartozó SEP értéket.
Ezután következik a függvény meghívása az összes mezőre:
d$SEP <- detectionpower(d$x, d$y)
Ez a kódsor egy újabb oszlopot ad hozzá a táblázatunkhoz, amelynek természetesen SEP a neve és minden mezőjébe bekerült a kiszámított SEP-érték.
A SEP-ről egy hasonló összefoglaló diagramot tudunk készíteni, mint a LEP-ről az előző részben.
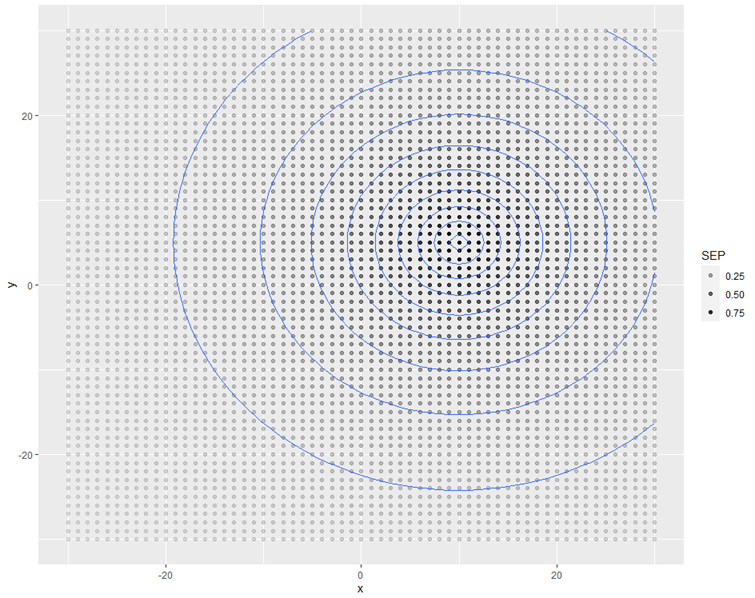
A teljesség kedvéért a fenti diagramot a következő kód segítségével ábrázoltam. Mint jól látható, ez a sor csak annyiban különbözik az előző részben részletesen ismertetett kódtól, hogy a LEP helyett a SEP határozza meg a pontok színét.
ggplot(d, aes(x = x, y = y, z = SEP)) + geom_point(aes(alpha = SEP)) + stat_contour(binwidth = 0.1)
Ahhoz, hogy megtaláljuk a keresett objektumot, két dolog kell. Az, hogy az objektum egy adott mezőben legyen (LEP), illetve abban a mezőben lehetőleg meg is találjuk (SEP), vagyis mindkét eseménynek teljesülnie kell! Emiatt az objektum megtalálásának a valószínűsége a LEP és a SEP szorzata. Innentől ezt már kisujjból kirázzuk:
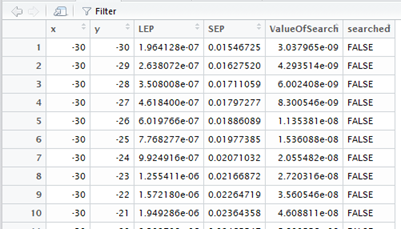
d$ValueOfSearch <- d$LEP * d$SEP
Így a táblázatunk egy újabb oszloppal lett gazdagabb.
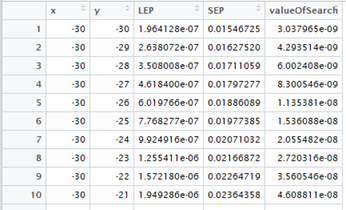
A ValueOfSearch oszlop értékeit a fentiekhez hasonló módon tudjuk ábrázolni:
ggplot(d, aes(x = x, y = y, z = d$ValueOfSearch)) + geom_point(aes(alpha = d$ValueOfSearch)) + stat_contour()
És az eredmény…
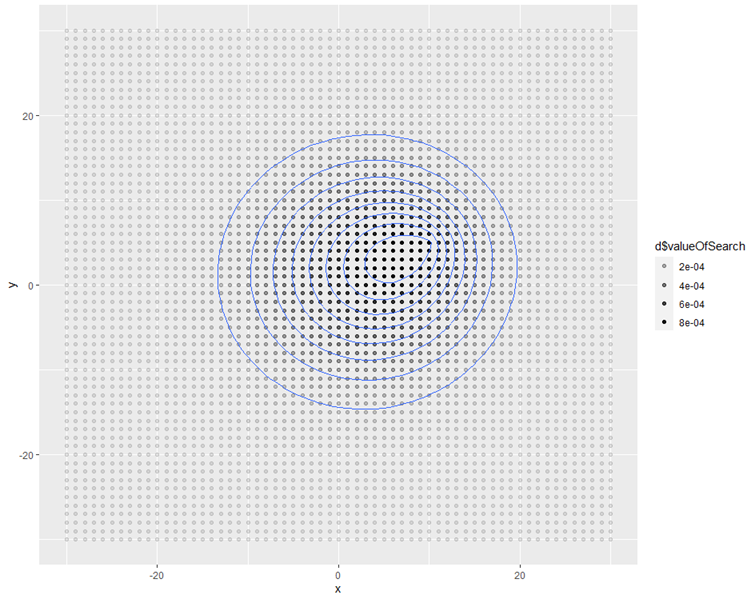
Ez a diagram mutatja meg nekünk azt, hogy ha a [0; 0] mezőben sejtjük a legnagyobb valószínűséggel a keresett objektumot, a detektor pedig a [10; 5] mezőben van, akkor melyik mezőben mekkora lesz az objektum megtalálásának a valószínűsége. Látható, hogy a „szintvonalak” egy kicsit eltorzultak, hiszen a ValueOfSearch mező létrehozása egyfajta „kettős középpontú” eloszlást hozott létre. Vajon melyik mezőben találhatjuk meg a legnagyobb valószínűséggel a keresett objektumot? A következő kóddal ezt is megtudhatjuk:
maxline <- which.max(d$ValueOfSearch)
maxx <- d[maxline, 1]
maxy <- d[maxline, 2]
maxx
maxy
A kód első sora kiválasztja a d adattáblának azt a sorát, amelyiknél a ValueOfSearch oszlopban lévő érték a legmagasabb, és a sor sorszámát beleteszi a maxline változóba. A második és a harmadik sorban pedig a maxx és a maxy változókba kiírja a maxline azonosítóval rendelkező sorban található x és y értéket, azaz a mező azonosítóját. Ezek alapján szimplán a maxx és a maxy változó nevét begépelve megkapjuk, hogy maxx = 7 és maxy = 3, azaz a keresett objektumot ebben a felállásban a [7; 3] mezőben találhatjuk meg a legnagyobb valószínűséggel a mindkét irányban -30-tól +30-ig számozott teljes területen.
És akkor most jön a neheze, hiszen most feltételezzük majd, hogy az előző diagram által kijelölt középpont környékén átkutatunk 100 darab mezőt. A 100 darab mező kutatási eredményei természetesen felülírják majd az összes mezőre vonatkozó ValueOfSearch értéket. Bayes tétele alapján egy adott mezőben a keresett objektum megtalálásának valószínűsége a következő képlettel adódik:
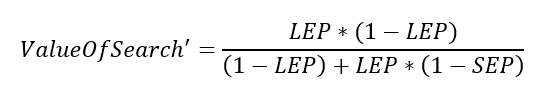
Aki végignézte a Bayes-tétel levezetéséről szóló videót (Egy teszt miért nem teszt – Bayes tétele vizuálisan (video)), az felfedezheti a Bayes-tétel egyes elemeit a fenti képletben. Ennek kiszámításához ismét írnunk kell egy függvényt, amely kiszámítja ValueOfSearch' értékét.
bayesUpdate <- function(searched, LEP, SEP) {
(LEP * (1 - searched * LEP))/(1 - LEP + LEP * (1 - SEP))
}
A bayesUpdate() függvénynek átadjuk az adott mezőre vonatkozó LEP és SEP értékét és egy searched nevű logikai változót is (erről később még írok majd). A függvény ez alapján kiszámolja a felülvizsgált ValueOfSearch'-t és ezzel az értékkel tér vissza.
Ha megvizsgáljuk a bayesUpdate() függvény kódját, azt látjuk, hogy a kicsit fentebb megállapított searched oszlop értékét is átadjuk paraméterként a függvénynek, sőt ez még a (LEP * (1 - searched * SEP))/(1 - LEP + LEP * (1 - SEP)) képletben is szerepel. Azaz a képlet más értéket ad vissza a 100 legmagasabb ValueOfSearch' értékkel rendelkező mező, illetve az összes többi mező esetében!
Mi változik?
Ha az adott mezőben a searched oszlop értéke TRUE (azaz 1), vagyis a mezőt átvizsgáltuk, akkor a képlet így néz ki:
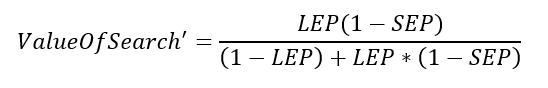
Ha a mező nincs a 100 átvizsgált mező között, akkor a searched oszlopban lévő érték FALSE (azaz 0), akkor viszont a képlet így néz ki:
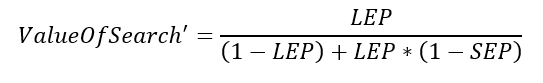
De miért is? Ha egy mezőben elvégeztem a keresést, akkor a megtalálási valószínűség (SEP) megegyezik a korábban meghatározott SEP-pel. Ha viszont egy mezőben nem hajtottunk végre keresést, akkor a SEP értéke értelemszerűen nulla, hiszen nem kerestünk az adott mezőben. A nevező viszont nem változik, hiszen Bayes tétele alapján a nevezőben a teljes eseménytér értéke található.
Mielőtt lefuttatjuk a bayesUpdate() függvényt, válasszuk ki a 100 mezőt, ahol a legnagyobb a találat valószínűsége. Ehhez egy kicsit trükkös kódsort alkalmazott a szerző.
d$searched <- rank(-1 * d$valueOfSearch) <= 100
Ez a kódsor létrehoz egy újabb oszlopot a d adattáblában. A rank() függvény egy adatsor minden egyes eleméhez hozzárendel egy sorszámot, amely megadja, hogy ha az elemeket nagyság szerint sorba rendeznénk, akkor az adott elem hányadik lenne. Vagyis megadja az adatsor elemeinek rangját. Ez esetben azt szeretnénk, hogy a ValueOfSearch oszlop azon elemei kapják a legkisebb sorszámokat, amelyeknek az értéke a legnagyobb! Ezért a rank() függvény zárójeles részében a ValueOfSearch oszlop értékeit megszorozzuk -1-gyel, így máris megfordul az elemek sorrendje. Vagyis az a 100 sor fogja kapni az 1..100 sorszámokat, amelyikek esetében a ValueOfSearch mező értéke a legnagyobb. Igen ám, de ha most megnézem a d adattáblát, akkor a searched oszlopban nem sorszámok, hanem FALSE és TRUE kifejezések szerepelnek!
Itt jön a trükk, ugyanis, ha a d$searched <- rank(-1 * d$valueOfSearch) kifejezés végére odabiggyesztjük a <= 100 kifejezést is, akkor innentől a fordító program ezt úgy értelmezi, hogy jelölje meg azokat a sorokat az IGAZ (TRUE) címkével amelyekre igaz, hogy a sorok előbb kiszámolt rangja kisebb, vagy egyenlő 100-al, a többit pedig jelölje HAMIS (FALSE) címkével. Nagyon tömör és ötletes kód, de aki ezt a trükköt nem ismeri, az megizzad, mire kitalálja, hogy mit is csinál. (Ezért írtam már máshol, hogy az R nem egy laza, egyszerűen kezelhető program…)
Miután ezt is tisztáztuk, nézzük az első 100 mező eredményét. Ehhez ismételten létrehozott a szerző egy új oszlopot a d adattáblában newSearchValue néven.
d$newValueOfSearch <- bayesUpdate(d$searched, d$LEP, d$SEP)
A parancs lefutása után a d adattáblában megjelenik egy új oszlop newSearchValue néven, ahol megjelennek a bayesUpdate() függvény segítségével kiszámolt valószínűségeket. Majd elfelejtettem megemlíteni, hogy természetesen az első 100 mező átkutatása nem hozott eredményt, különben az egész keresésünk véget érne.
A befejező részben végül megnézzük majd, hogyan változnak majd a keresési valószínűségek, ahogy egymás után újra és újra átvizsgáljuk a legnagyobb valószínűséggel rendelkező mezőket.
Források:
R-Bloggers – Bayesian Search Models
https://www.r-bloggers.com/2014/03/bayesian-search-models/
Hadley Wickham: Elegant Graphics for Data Analysis, Springer, 2016
https://ggplot2-book.org/index.html
R ggplot2 cheat sheet
https://rstudio.com/wp-content/uploads/2015/03/ggplot2-cheatsheet.pdf




