(Vissza az előző részhez…)

Az előző héten ott hagytam abba, hogy elkészítettem egy darab iterációt az első 100 mező keresése alapján, ahol a legnagyobb valószínűséggel vártuk a keresett objektumot. A befejező részben eljutok majd oda, hogy a teljes keresési folyamat láthatóvá válik.

Ezt viszont úgy szeretném megtenni, hogy egymás mellé tegyem az eredeti és a 100 mező keresése által felülvizsgált adatokat. Ehhez sajnos szükség lesz némi adatmanipulációra. Ez azért bosszantó, mert erre nem a feladat végrehajtása miatt van szükség, hanem mert a ggplot2 grafikai utasításai kötött formában kérik az adatokat, nem lehet csak úgy akárhogyan felépülnie az adattáblának.

Ehhez arra van szükség, hogy a d adattáblánkat egy kicsit átalakítsuk. Ehhez létrehozunk egy nd nevű új adattáblát (lásd a fenti kódot). Ennek az a célja, hogy a ValueOfSearch és a newValueOfSearch mezők adatai egy közös oszlopba kerüljenek és a search mezőben lévő TRUE és FALSE értékek alapján legyenek kettéválasztva. Ez a kódsor ismét eléggé összetettre sikeredett, így az egyes kódrészleteket részekre bontva fogom bemutatni. Lássuk az első sort…

A kódrészlet eleje már ismerős, létrehozunk nd néven egy adattáblát, majd a zárójelben el kezdjük létrehozni a tábla oszlopait. Az x és az y oszlopokba belemásoljuk a d adattábla x és y oszlopait (d$x és d$y), de a korábban már tárgyalt rep() függvény segítségével kétszer egymás alá! Erre azért van szükség, hogy később a ValueOfSearch és a newValueOfSearch mezők ugyanúgy beazonosíthatók legyenek azután is, hogy azonos oszlopba másoltuk őket, mint ahogy a d adattáblában eddig.

Ez a sor annyit tesz, hogy az nd adattábla valueOfSearch oszlopába egymás alá másolja a d adattábla ValueOfSearch és newValueOfSearch oszlopait.

Ez a sor a searched oszlop adatait is megduplázza majd egymás alá másolja a két egyforma adatsort.

Az utolsó sor pedig létrehoz egy search nevű oszlopot, majd a sorok felét feltölti azzal, hogy „Before Any Search”, azaz minden keresés előtt, majd a második felét azzal, hogy „First Wave”, azaz első hullám. Ezt ugye azzal a módszerrel teszi, hogy a c() függvénnyel készít egy kételemű mátrixot, majd a mátrix mindkét elemét sorban annyiszor belemásolja a search oszlopba, amennyi a d adattábla sorainak száma. Ezt az nrow() függvény segítségével adja meg.

Így el is készült az új nd adattábla, amelynek a segítségével el tudjuk készíteni a fent említett diagramot, amely egymásra tudja tenni az első keresés előtti és utáni állapotot.

A korábbi hasonló diagramokhoz képest igazából csak egyetlen függvényhívásban van különbség, ez a facet_grid() függvény. Ez hozza létre azt a rácsot, amelyben a két diagramot egymás mellé tudjuk helyezni. A ggplot2 csomagban nem lehet csak úgy megrajzolni előre egy rácsot, amibe bele illesztjük a grafikonokat, a függvény ezt a rácsot automatikusan hozza létre egy „csoportosító” oszlop alapján, amely jelen esetben a search oszlop, amit egy kicsit fentebb hoztunk létre arra, hogy elválassza a 100 keresés előtti és utáni adatokat. A ~ operátor azt jelenti, hogy valamelyik mezőnek a függvényében ábrázolja a ggplot függvény az adatokat. A . operátor pedig arra utasítja a függvényt, hogy a teljes adattáblát, vagyis az összes oszlopot – természetesen a search mezőt kivéve – használja fel a grafikon elkészítésekor.

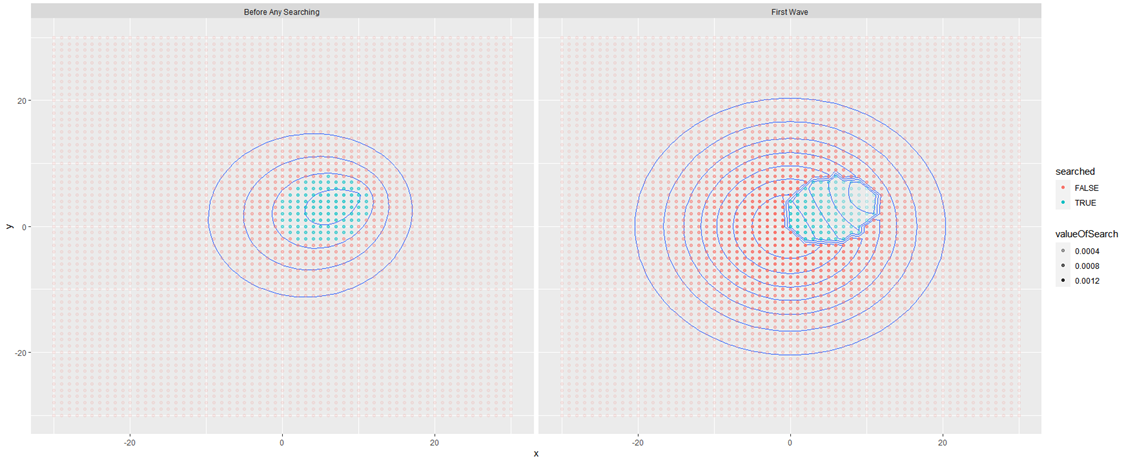
Mit is látunk ezen a diagramon. A bal oldalon vannak a keresés előtti, a jobb oldalon a keresés utáni adatok. A jobb oldali diagramon található folt a 100 mező, amelyen a keresést végrehajtottuk. Látható, hogy ezen a területen a „magasságvonalak” megváltoztak, nyilván a keresés eredményeinek megfelelően. Érdekes, hogy annak ellenére, hogy a keresett mezőkben nem találtuk meg a keresett objektumot, az objektum megtalálásának valószínűsége nem változott nullára! Persze, hiszen attól, hogy nem találtuk meg az objektumot ezekben a mezőkben, attól még ott lehetnek, mert a detektálás valószínűsége sem 100%. Elképzelhető, hogy az objektum ott van valamelyik mezőben, csak nem találtuk meg! További megfigyelés még, hogy a nem keresett mezők esetében a „magasságvonalak” kiterjedése megnőtt. Azzal, hogy a keresés középpontjában lévő mezőkben nem találtuk meg az objektumot, egy kicsit megnőtt annak a valószínűsége, hogy esetleg a távolabbi mezők valamelyikében fogjuk megtalálni, amit keresünk.

Végül jöjjön a legjobb rész. Itt azt szeretném bemutatni, hogyan változik a keresési terület annak függvényében, hogy a fenti algoritmust fegyelmezetten betartva újra és újra átvizsgáljuk azt a 100 mezőt, ahol a keresett objektum megtalálási valószínűsége a legnagyobb. A célom az, hogy lefuttatok 1000 darab 100 mezős keresést és megnézem, hogyan változnak majd a keresési valószínűségek az egyes mezőkben.

Először is érdemes létrehozni egy néhány táblát, amelyekben a keresési ciklusok közben keletkezett adatokat fogjuk tárolni. Először is hozzunk létre egy searchCount nevű tömböt (egy oszlopból álló táblázatot), amely pontosan annyi elemből fog állni, mint a d adattábla, azaz a keresési terület minden egyes mezőjéhez fog egy elem csatlakozni. A későbbiekben látni fogjuk, hogy ebbe a tömbbe fogjuk eltárolni, hogy az egyes mezőket hányszor jelöltük ki keresésre a keresési ciklusok során.

A következő lépésben létrehozásra kerül két 1000 elemű tömb, amelyben majd a LEP és a SEP értékeit fogjuk elmenteni. A probInSearchArea fogja tartalmazni a LEP, a probFindInGrid pedig a SEP értékeit. Ezekbe a tömbökbe a LEP és a SEP összesített értékeit fogjuk elmenteni a keresett objektum ÖSSZESÍTETT megtalálási valószínűségeit. Az ezekben eltárolt értékek a későbbiekben megmutatják majd, hogyan csökken a megtalálás valószínűsége, ahogy egyre több mezőt egyre többször vizsgálunk át. Ez egy fontos része lesz majd a módszernek, mert ezek segítségével tudjuk majd meghatározni azt, hogy mikor érdemes abbahagyni a keresést.

A következő lépésben létrehozzuk a ValueOfSearch és a SEP értékeihez tartozó kiinduló adatok mátrixát és feltöltjük a d adattáblában már kiszámított értékeivel.

Most pedig kezdődjön az 1000 darab 100 mezős keresés ciklusa:

Nézzük részletesen, mit is csinál a kód.

Az első sorban a klasszikus ciklus programozásnak megfelelően létrehozunk egy i változót, majd megkérjük az R-t, hogy ismételje meg a {} zárójelben lévő műveleteket úgy, hogy i értékéhez minden ciklusban hozzáad egyet.

A kapcsos zárójelen belül az első sorral már találkoztunk korábban, itt választjuk ki a 100 vizsgált mezőt, ahol a találati valószínűség a legnagyobb.

Ez a sor már több magyarázatot igényel. Korábban már tisztáztuk, hogy az előző sorban létrehozott searchLocations tömb logikai (TRUE és FALSE) értékeket tartalmaz. Ezt hogyan tudjuk hozzáadni egy másik tömbhöz? Úgy, hogy a FALSE érték 0-t, a TRUE érték pedig 1-et jelent az R számára, így már értelmezhető a dolog. Mivel a searchCount tömböt a cikluson kívül definiáltuk és minden egyes elemét feltöltöttük nullákkal, de később a cikluson belül már nem nullázzuk, ezért ebben a tömbben gyűjtjük, hogy a keresési ciklusok során melyik mezőt hányszor kutattuk át.

Ahogy azt fentebb tisztáztam, ebbe a két tömbbe mentjük el azt, hogy az egyes 100 mezős keresési ciklusok végén hogyan változik a keresés teljes megtalálási és detektálási valószínűsége.  

Végül a ciklus előtt definiált p0 tömbben tárolt valószínűségeket a korábban már használt bayesUpdate() függvény segítségével elvégezzük a valószínűségek frissítését. Ez a frissítés is kummulált lesz, hiszen a p0 tömb is a ciklus előtt került létrehozásra. Az az érdekes, hogy a keresési algoritmus szempontjából ez az egy sor a lényeges, az összes többi kód csak valamiféle adatgyűjtésre szolgál.

A diagram ez esetben viszont egy kicsit mást fog nekünk megmutatni, a pontok árnyalata nem a keresési valószínűséget fogja ábrázolni, hanem azt, hogy melyik mezőt hányszor kutattuk át. Ezzel jobban szemléltethető a keresési folyamat előrehaladása. Ezért is gyűjtöttük a searchCount tömbben, hogy az egyes mezőket hányszor kutattuk át. A tömb elemeihez most hozzárendeljük a mezők x és y koordinátáit.

A korábban már ismert pontdiagramot most az nSearches adattábla alapján hozzuk létre.

Ez természetesen egy állóképet fog kirajzolni, de a keresési folyamat jobb szemléltetése érdekében több fázisdiagramot is kinyomtattam, amelyeket összefűztem egy kis animációvá.

Az animáció jól mutatja, ahogyan a keresés elindul az eredeti középpontból és a sötét pontok (minél sötétebb egy pont, annál többször kutattuk át azt a mezőt) hogyan haladnak a keresési terület bal széle felé. Az is kiderül, hogy mintha kialakulna egy második keresési központ az ábra bal alsó sarka közelében.

A legvégén nézzük meg azt, hogy hogyan lehet megállapítani, meddig érdemes folytatni a keresést. Azt mondtuk, hogy az összegzett keresési valószínűségek alapján meg tudjuk mondani, hogy egy adott keresési ciklus végrehajtása után mennyivel csökken a keresett objektum megtalálásának esélye. Ehhez ismét adattáblává alakítjuk az eredetileg tömbként definiált probInSearchArea változót egyszerűen csak úgy, hogy egy másik oszlopban mellé tesszük az ismétlések sorszámát.

Az így kapott searchValue változó segítségével ábrázolom majd egy újabb grafikonon az összegzett megtalálási valószínűség változását ciklusról ciklusra.

És íme a diagram.

A diagramból azt olvashatjuk ki, hogy az első keresési ciklusok után meredeken zuhan a megtalálás esélye, majd kb. 250 keresés után már annyira kicsi ez a valószínűség, hogy itt már nem érdemes folytatni, hiszen a keresésbe fordított erőforrások mennyisége már nem áll arányban a várható eredménnyel.

Összegzés:

Ez egy egészen komplex feladat volt, még úgy is, hogy nem én írtam a kódot, csak kipróbáltam, amit valaki más megírt. Igyekeztem annyira részletesen leírni a teendőket, hogy a kód minden részletét meg lehessen érteni és követni lehessen, ahogy a módszer körről – körre felülvizsgálódnak a mezők találati valószínűségei és követhető legyen az egész feladat. Bár így egy kicsit bonyolultnak tűnik, szerintem egy egyszerűbb példa esetében kézzel is kiszámolhatók az eredmények, amelyek az ismétlések során keletkeznek. Csak persze egy egyszerűbb probléma esetén nem igazán van értelme egy ilyen bonyolult algoritmust alkalmazni. A megoldás menete és a programsorok alapján az a benyomásom, hogy olyan valaki írta, aki igen tapasztalt és jól ismeri az R környezetet, bevallom én nem tudtam volna így megírni. De nem is ez a lényeg, inkább az, hogy abban az igen ritka esetben, ha valakinek pont erre lenne szüksége, ezen leírás alapján a módszer rekonstruálható és adaptálható.

Aki pedig hobbiból tanulmányozza az r-t, mint ahogy én is, csak azt tudom javasolni, hogy másolja be az idézett programrészleteket az RStudio-ba és lépésenként menjen végig a folyamaton, nézze meg, hogy melyik tömbben és adattáblában mi történik, nagyon sokat lehet belőle tanulni.

Jó szórakozást! (Ha bírod idegekkel) :-)

Források:

R-Bloggers – Bayesian Search Models
https://www.r-bloggers.com/2014/03/bayesian-search-models/

Hadley Wickham: Elegant Graphics for Data Analysis, Springer, 2016
https://ggplot2-book.org/index.html

R ggplot2 cheat sheet
https://rstudio.com/wp-content/uploads/2015/03/ggplot2-cheatsheet.pdf