
Az előző hetek során megpróbáltam részletesen bemutatni a Bayes-tételére alapuló keresési algoritmus részleteit (Szimat, szimat …! – Bayes-i keresési algoritmus R-ben - 1. rész), de úgy tűnik, hogy egy kicsit "meghaltam a szépségben", a módszer lényege elveszett a rengeteg adatmanipuláció és diagramrajzolás között.
Ezzel kapcsolatban teljesen egyetértek a kapott kommentekkel és nem kis lelkiismeretfurdalásom van a dolog miatt. Úgy döntöttem, hogy még egyszer nekiszaladok a témának - noha el tudom képzelni, hogy már unalmas a téma. Fordulo_bogyo javaslatára kidolgoztam egy egyszerűbb példát. Készítettem egy 10x10 táblázatot és minden egyes mezőnek adtam két valószínűségi értéket.
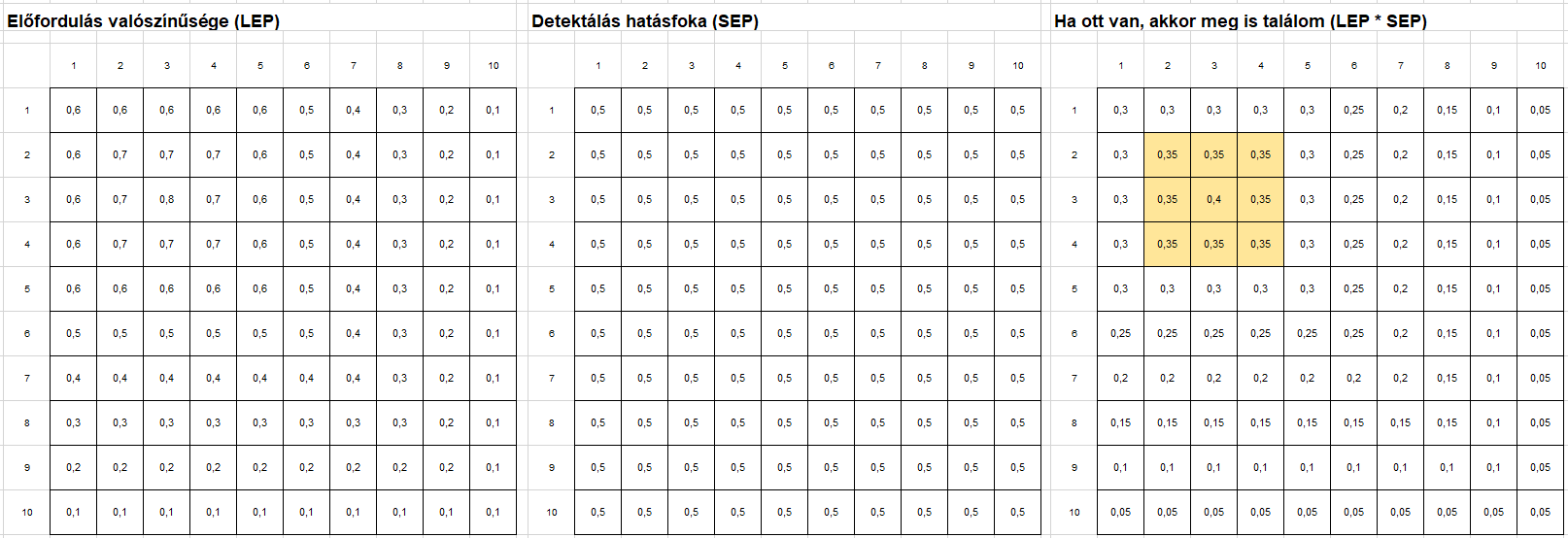
- Az első annak a valószínűsége, hogy a keresett tárgy az adott mezőben található. Ezt továbbra is LEP-nek hívom, bár ennek így most nincs jelentősége a kalkuláció szempontjából, csak a követhetőséget szeretném biztosítani a korábbi cikkekkel. Itt egyetlen dolgot változtattam meg fordulo_bogyo javaslatához képest, a tárgy megtalálásának valószínűsége nem egyforma az összes mezőben, van egy kijelölt mező (a 3:3 koordinátájú), amely esetében a leginkább sejtjük, hogy a keresett tárgy ott lehet. Itt úgy döntöttem, hogy a tárgy 80%-os valószínűséggel található ebben a mezőben. A szomszédos mezőkben az előfordulás valószínűsége 10%-al kisebb, majd minél messzebb kerülünk ettől a mezőtől, annál kisebb lesz ez az esély.
- A második a detektálás valószínűsége, vagyis annak, hogy ha a keresett tárgy az adott mezőben van, akkor megtalálom. Ezt fordulo_bogyo javaslatára egyöntetűen 0,5-re állítottam be.
- Ezek alapján annak a valószínűsége, hogy a keresett tárgy abban a mezőben van, ahol keressük és meg is találjuk, a fenti két valószínűség szorzataként adódik.
Itt látható a kiinduló állapot. A jobb oldali táblázatban látható zöld mezőkben fogom kezdeni a keresést, mert ezekben a legnagyobb a keresett tárgy megtalálásának az esélye.
Az egyik korábbi cikkben (Tapogatózás a sötétben – Bayes-i keresési algoritmus R-ben - 2. rész) már elmagyaráztam, hogy minen egyes keresési kör után minden egyes mező esetében újra ki kell számolni a megtalálás valószínűségét (LEP*SEP), de ez esetben a Bayes-tétel segítségével. A képleteket egy kicsit másképp írtam fel, ami talán az egyik leginkább félrevezető része volt a korábbi cikkeknek.
Ha az adott mezőben kerestük a tárgyat, akkor a következő képletet kell alkalmaznunk:
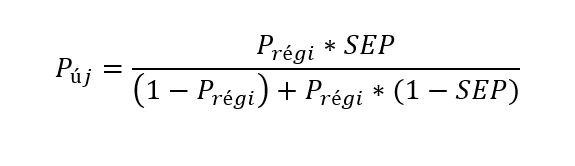
Ha viszont nem keresünk az adott mezőben, akkor viszont ezt használjuk:
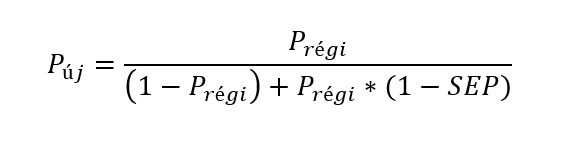
A két képlet tulajdonképpen egyetlen dologban különbözik a régebbi cikkek képleteitől és ez az, hogy a 'LEP' kifejezés helyett a 'Prégi' kifejezést használom. Ez a forma sokkal jobban kifejezi azt, ami most következni fog, illetve (legalábbis remélem) az előző cikkeben leírt R-kód megértésében is segíteni fog.
Először is létrehoztam egy újabb táblázatot a mezőkről, amelyekbe a fenti képletek segítségével kiszámítom majd a keresések eredménye alapján felülvizsgált megtalálási valószínűségeket.
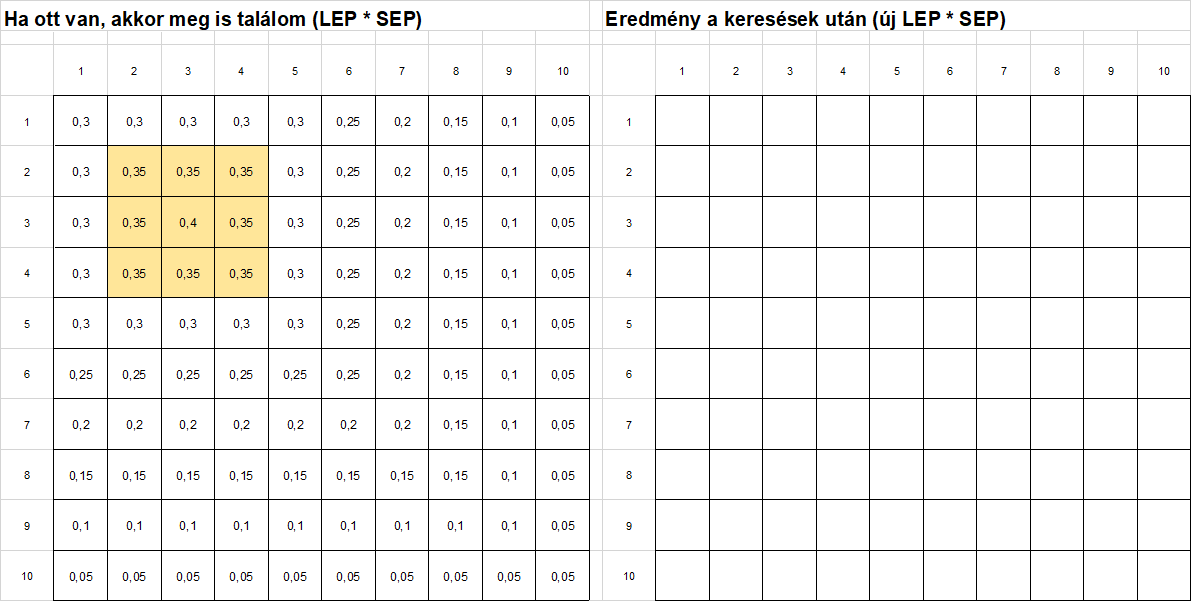
Az új táblázatban megjelöltem azokat a mezőket, amelyekben keresni fogok. Nagyon fontos, hogy ne tévesszem el, hogy melyik mezőkbe melyik képletet fogom beírni, ezért jó, ha színnel is megkülönböztetem őket.
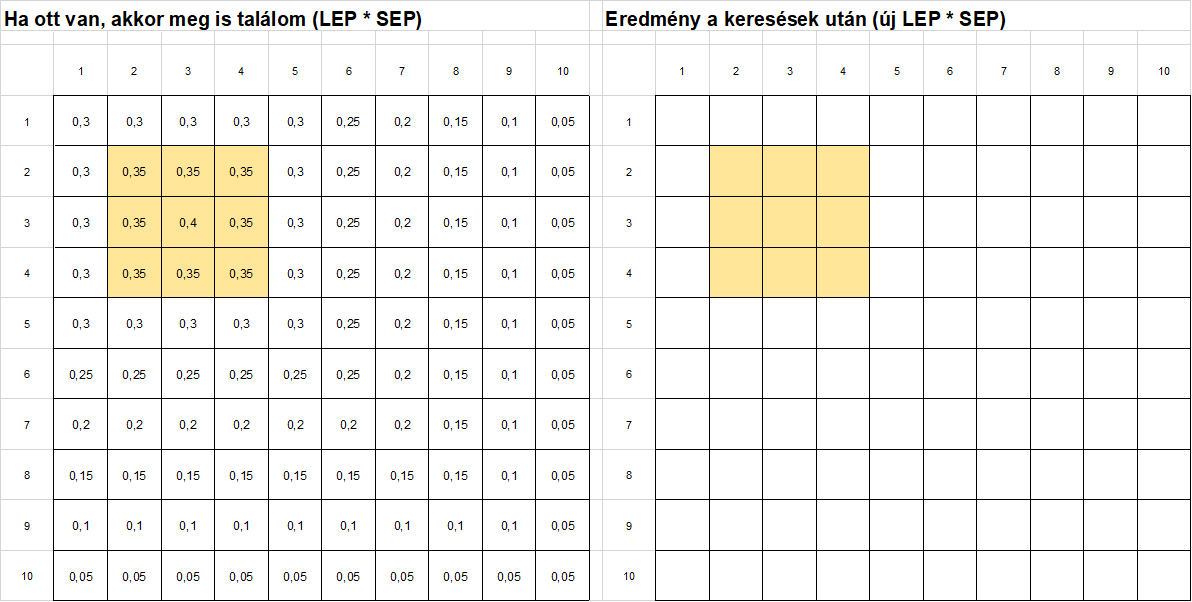
Ezután a zöld színnel jelölt mezőket kitöltöm az első képlettel kiszámolt új valószínűséget. A mezőbe beírt konkrét képletet nem írom ide, mert a teljes excel file-t le tudod tölteni a cikk végén található linken.

Ez lett e kitöltés eredménye.
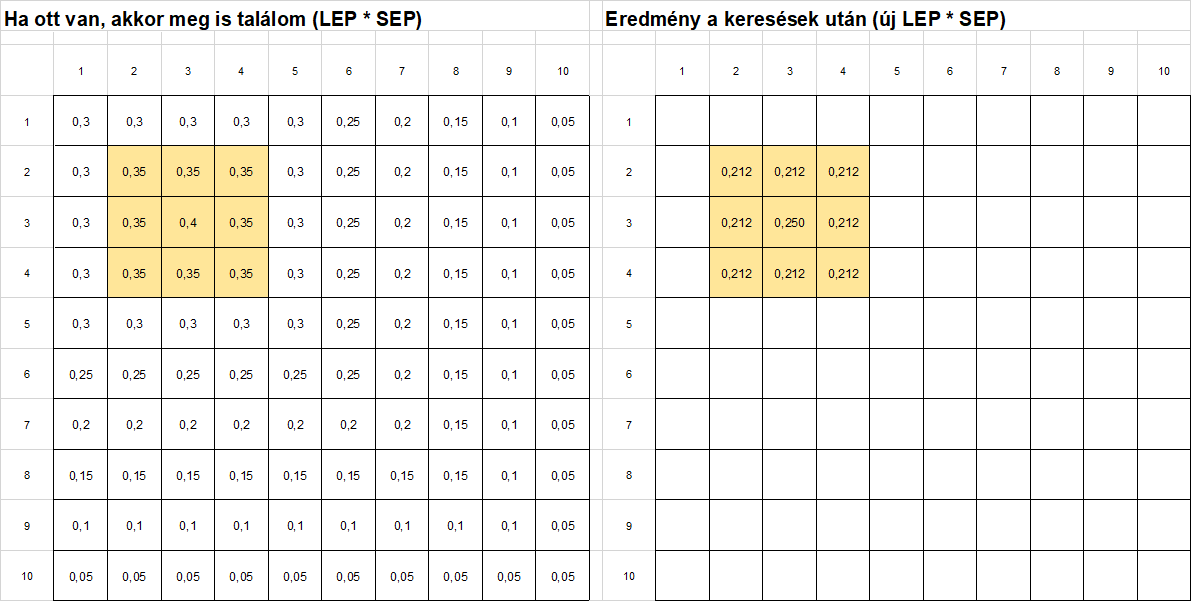
Ezután a második képlettel kitöltöttem a többi mezőt, amelyekben nem kerestem a keresett tárgyat.
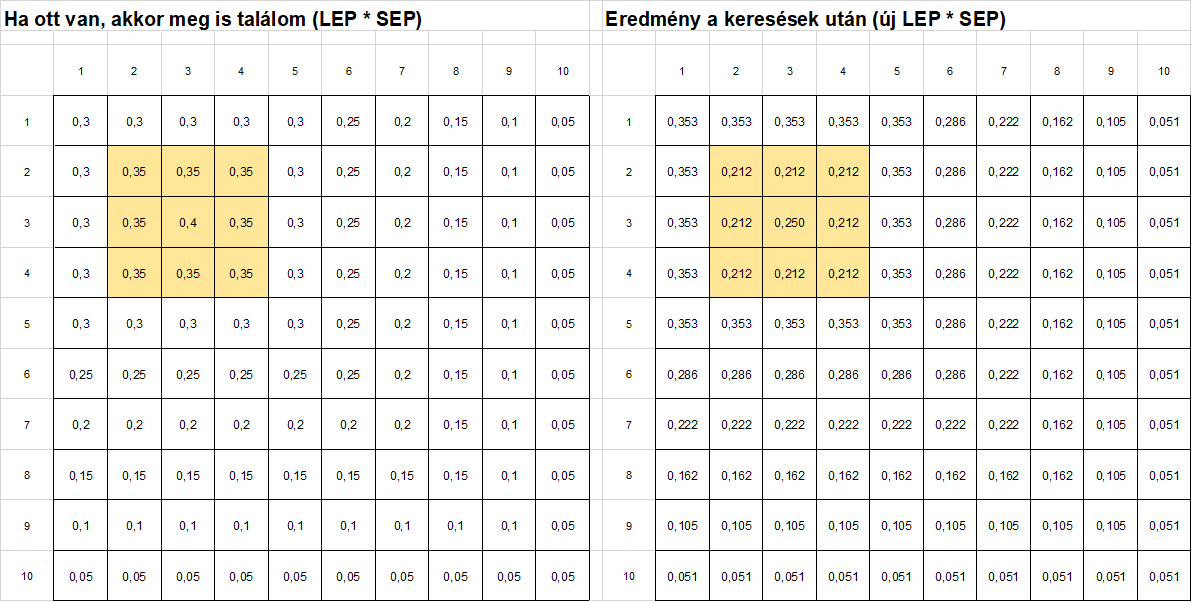
Majdnem készen vagyok az első keresési kör eredményével, már csak a legmagasabb megtalálási valószínűségű mezőket kell kiválasztanom. Ezt a feltételes formázás parancs segítségével tudom megtenni, mert van egy olyan opció, amellyel meg tudom változtatni a legnagyobb értékkel rendelkező 10% színét. Ehhez kijelölöm az új táblázatot és a feltételes formázásnál kijelölöm, hogy a táblázatkezelő változtassa meg azoknak a celláknak a színét, amelyek beletartoznak a legmagasabb valószínűségű 10%-ba.
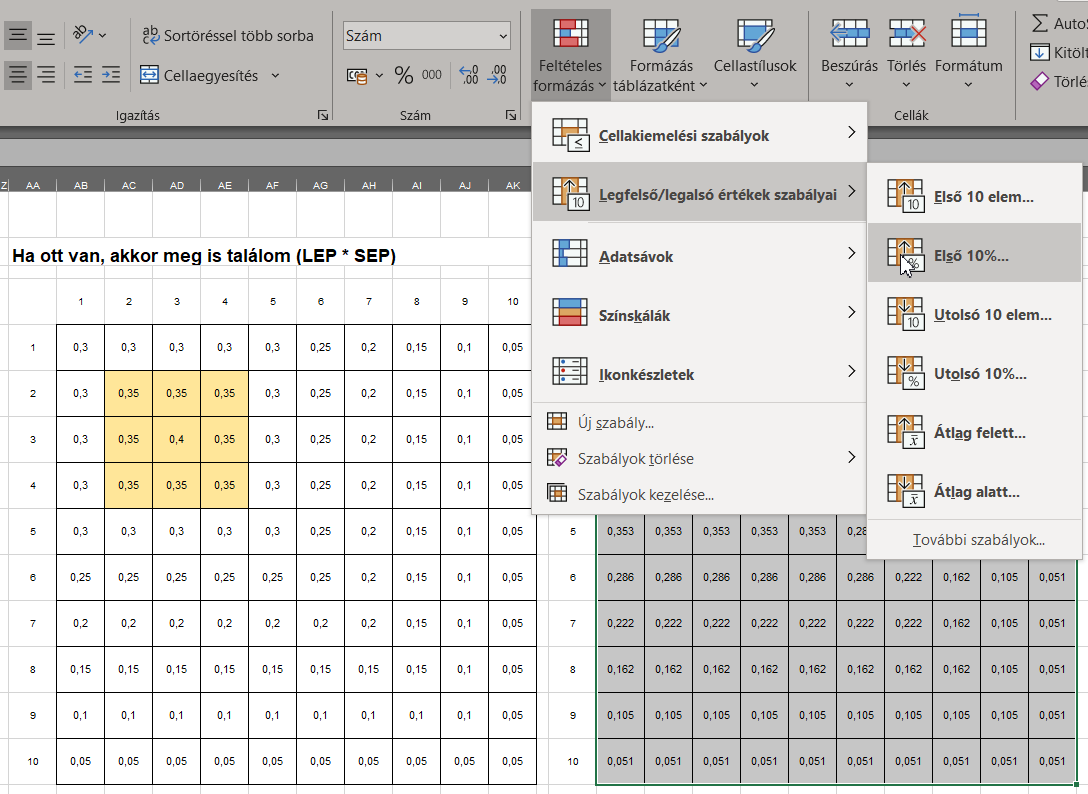
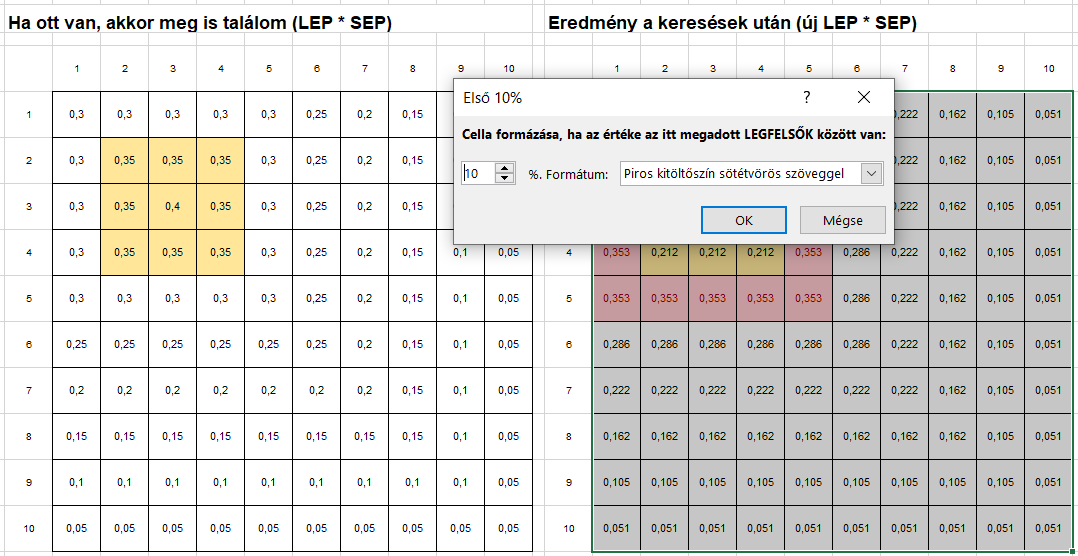
A korábban kézzel zöldre színezett mezők színét eltávolítva megkapjuk az első kör eredményét.
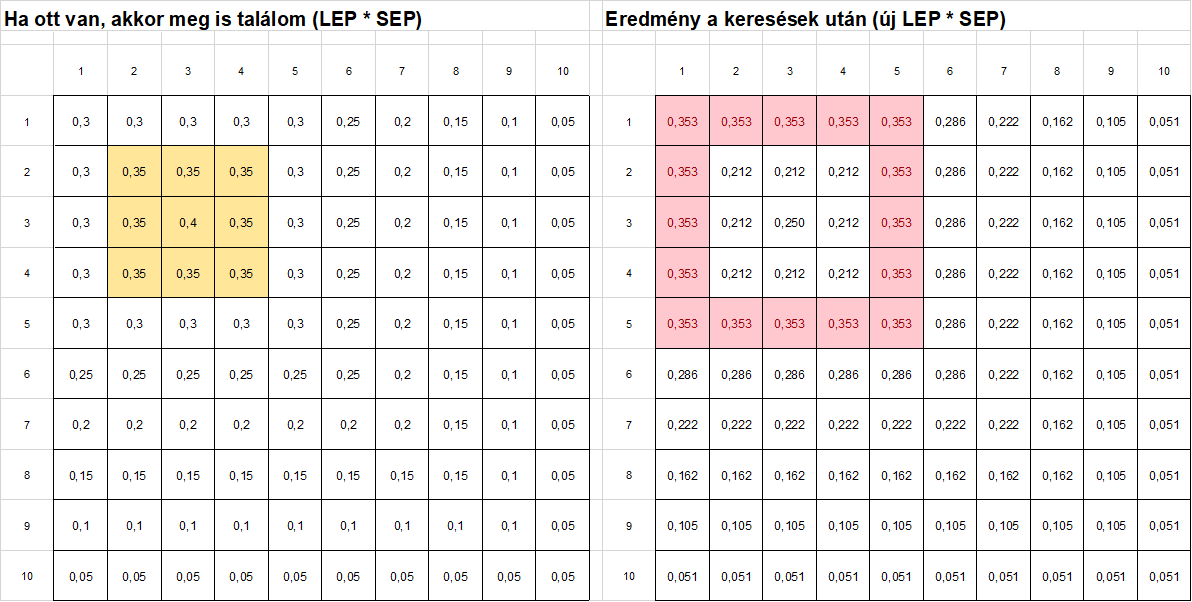
Mit láthatunk az eredményekből. Ha összehasonlítjuk azokat a cellákat, amelyekben a keresést végeztük az első körben, azt látjuk, hogy ezekben a megtalálási valószínűség csökkent. Ez érthető is, hiszen ezeket most megnéztük, de a keresett tárgyat nem találtuk, így azt gondolhatjuk, hogy itt már egyszer kerestük, vagyis kisebb lett a valószínűsége annak, hogy itt van a keresett tárgy. Azokban a mezőkben, ahol nem végeztünk keresést, ott viszont nőtt a megtalálási valószínűség, hiszen amikor nem találtuk meg a tárgyat a keresés során, figyelmünk a nem keresett mezők felé fordul.
A második keresési körben azokat a cellákat fogjuk átvizsgálni, amelyek az első keresési kör végén ki lettek jelölve. Ehhez lemásoltam az előző lapot és elneveztem '2'-nek. Ezután az első kör eredményét átmásoltam a bal oldalra, de úgy, hogy csak a cellák értékét másoltam át, a képletet nem.
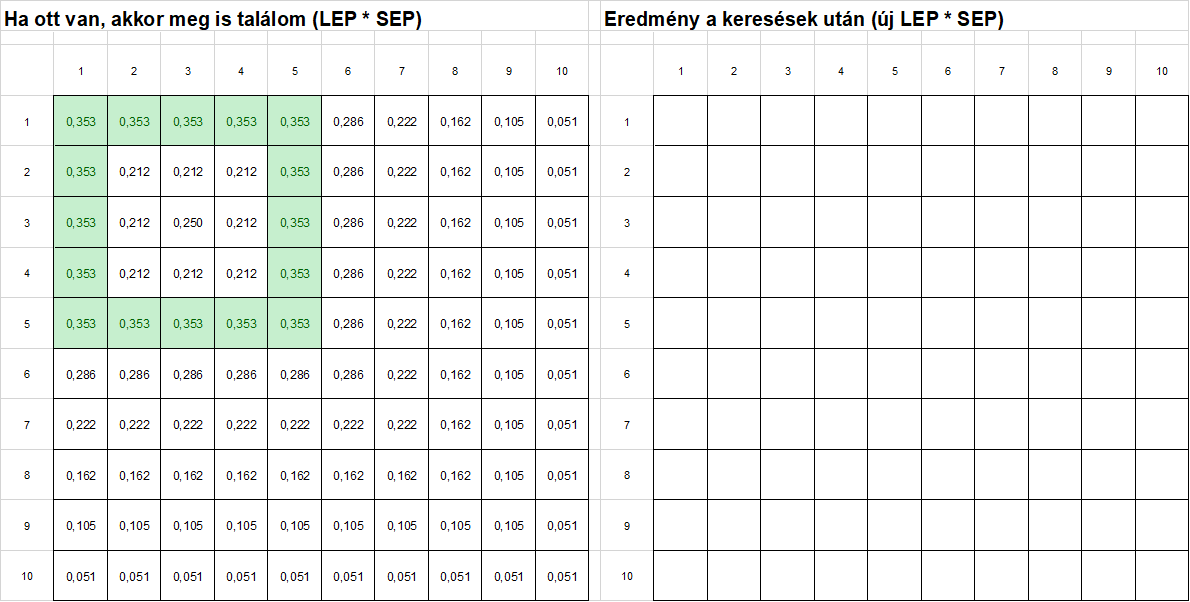
Ismét kijelöltem kézzel az átvizsgálandó cellákat, ...

..., majd az első körhöz hasonlóan kitöltöttem a mezőket a megfelelő képletekkel, és újra kijelöltem a legnagyobb valószínűségű 10%-ot.

És ezt a folyamatot még megismételtem még további 17 alkalommal. Mivel a keresett tárgyat nem találtuk meg, a folyamat eredménye az lett, hogy a keresési mezők szépen folyamatosan áttevődtek az eredeti középponttól messzebb eső mezőkre. Az viszont igaz, hogy eközben volt jó néhány feleslegesnek látszó keresési kör, amikor az algoritmus visszatért a korábban már átvizsgált mezőkre. Ez lehet zavaró, de engem arra emlékeztet, amikor keresek valamit, nem találom, ezért többször is megnézem ugyanazt a helyet, hátha ott van, amit keresek, csak nem vettem észre.
Ha nem akarsz elmélyedni az excel file részleteiben, akkor feltettem a youtube-ra egy videót a keresési folyamatról.
A szimuláció eredményéről készült rövid videót itt találod.
Ha viszont érdekel az excel file, amit készítettem, akkor innen le tudod tölteni.
A szimulációt tartalmazó excel file itt található.
Összegzés:
Nagyon sajnálom, hogy a korábbi cikkekben nem sikerült átadni a módszer lényegét. Remélem ebben a cikkben sikerült érthetőbben illusztrálnom, hogy miről szól ez a módszer. Az excel file segítségével pedig el lehet kezdeni játszadozni, hogy mi történik, ha megváltoztatsz ezt-azt. Örülök a kommenteknek, amelyekben jeleztétek, hogy nem értitek, amit írtam, mert ez inspirált arra, hogy elkészítsem ezt a cikket. Ezek nélkül valószínűleg nem született volna meg ez az excel file, mert eszembe se jutott volna még jobban belemenni a részletekbe.
Külön köszönöm a kommentek udvarias és korrekt stílusát, a jogos észrevételeket minden esetben megfontolom és változtatok, ha tudok.





