Most, hogy így az elmúlt hetekben elmélyedtem az egymintás Z-próbában, ismét felmerült bennem a kérdés, hogy miért kell a six sigma projektekben mindig ellenőrizni, hogy a minta eloszlása normál eloszlást követ. Például a Vargha András ezt írja a ’Matematikai statisztika pszichológiai, nyelvészeti és biológiai alkalmazásokkal’ című könyvének 157. oldalán.
… Az u-próba (Z-próba. a szerk.) olyan szakmai problémák esetén alkalmazható, amikor van egy olyan kvantitatív X változónk,
- amelyről tudjuk, hogy normál eloszlású,
- amelynek ismerjük az elméleti szórását (σ),
- és amelyről van egy feltételezésünk, hogy mi lehet az elméleti átlaga …
Most tényleg nem kötözködni szeretnék, hanem meg szeretném érteni, hogy ha a Centrális Határeloszlás tétele (A nagy dobókocka kísérlet) igaz, és empirikusan is igazolható, hogy teljesen mindegy, milyen a sokaság szórása, amelyből kivettem a mintát, akkor miért kellene a sokaságnak normál eloszlásúnak lennie. Arról nem is beszélve, hogy egy ilyen feltétel nem tartható be, merthogy a sokaságot nem ismerem, így be sem tudom bizonyítani, hogy normál eloszlású. Ráadásul a sokaságból kivett nagyszámú minta eloszlását sem ismerem, hiszen a sokaságból kizárólag egyetlen mintát vettem ki, tehát azt sem tudom, hogy a mintaátlagok eloszlása milyen. Az egyetlen dolog, ami rendelkezésemre áll, az a minta. Ennek ismerem az elemeit, de tulajdonképpen a minta elemeinek eloszlása az egyetlen, ami az egymintás Z-próba esetén egyáltalán nem érdekel.
Jó, de akkor mit jelent a fenti feltételezés? Szerintem ebben a formájában semmit. A különféle statisztika könyvek és weboldalak által előszeretettel citált feltétel valójában azt feltételezi, hogy a Centrális Határeloszlás tétele alapján feltételezzük, hogy a bármilyen eloszlású sokaságból kivett nagyszámú minta átlagainak eloszlása normál eloszlású. Ezt valójában nem tudjuk, hiszen – ahogy azt már fentebb is leírtam – nem veszünk ki ötezer darab mintát a sokaságból csak azért, hogy bebizonyítsuk, hogy a mintaátlagok eloszlása normál eloszlású. Ez az, amit valójában feltételezünk, mert ha a mintaátlagok átlagai nem követnék a normál eloszlást, akkor az teszt veszítené el az értelmét.
De mi is a kockázat ebben az esetben? A Centrális Határeloszlás tétele nagy elemszámú minták esetében egészen jól működik, ez akár matematikailag bizonyítva, akár számítógépes szimulációkkal tesztelgetve bizonyítható. A kérdés például akkor vetődhet fel, ha a sokaság feltételezett eloszlása erősen aszimmetrikus, és a kivett minta elemszáma nem elég nagy. Az szimmetria hiánya azért lehet probléma, mert ha nem elég nagy a minta elemszáma, akkor jelentősen megnő az esélye annak, hogy a mintaátlagok eloszlása is enyhén aszimmetrikussá válik. Nézzük meg ezt egy példán keresztül.
De mielőtt hozzákezdünk, töltsük be a szükséges csomagokat.
library(ggpubr)
library(nortest)
library(BSDA)
library(gridExtra)
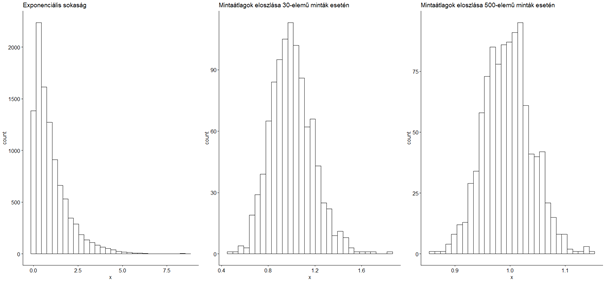
Vegyünk egy tényleg erősen aszimmetrikus sokaságot, mondjuk egy olyat, ahol a sokaság értékei exponenciális eloszlás szerint változnak.
#10000 elemű sokaság létrehozása
expSokasag <- rexp(10000, rate = 1)
#hisztogram készítése a 10000 elemű sokaságról
plot1 <- gghistogram(expSokasag, title = "Exponenciális sokaság")
#hisztogram kirajzolása
plot1
A sokaságunk neve legyen ’expSokasag’. A fenti parancssor első sora az ’rexp()’ függvény segítségével készít egy 10 000 darab véletlen számból álló adatsort (vektort), ahol az exponenciális függvény lambda paramétere 1. A második sor készít egy hisztogramot a kapott 10 000 szám eloszlásáról és elmenti azt a ’plot1’ változóba. A ’title = „Sokaság”’ paraméter adja meg, hogy a diagram címe legyen Sokaság. A harmadik sorban a ’plot1’ változó begépelésével kirajzolódik a hisztogram.
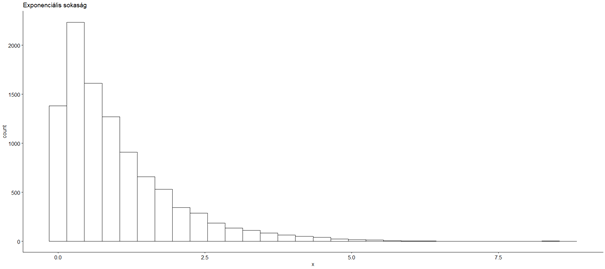
A hisztogramról jól érzékelhető, hogy az alacsonyabb értékek jelentősen gyakrabban fordulnak elő, mint a magasabbak. Most vegyünk ezekből 1000 darab mintát és mentsük el a minták átlagát (a kódsor értelmezését megtalálod a „Senki többet harmadszor? – Újra az egymintás Z-próbáról, most R-kóddal” című cikkben).
#Az exponenciális sokaságból kivett minták átlagát tartalmazó vektor létrehozása
expMintaAtlagok <- c()
#ciklus a minták létrehozására és az átlagok elmentésére
for (i in 1:1000)
{
#30-elemű véletlenszerű minta a sokaságból
minta <- sample(expSokasag, 30, replace = FALSE)
#a kivett minta átlagának elmentése az 'atlag' változóba
atlag <- mean(minta)
#az 'atlag' változó értékének hozzáadása a 'MintaAtlagok' vektorhoz
expMintaAtlagok <- c(expMintaAtlagok, atlag)
#a számláló léptetése eggyel
i <- i + 1
}
#A mintaátlagok hisztogramjának kirajzolása
plot2 <- gghistogram(expMintaAtlagok, title = "Mintaátlagok")
#hisztogram kirajzolása
plot2

A hisztogram láttán az az érzésünk támadhat, hogy az értékek enyhén aszimmetrikusan helyezkednek el, de azért ez nem teljesen nyilvánvaló, inkább csak egy sejtés. Győződjünk meg erről a már jól megtanult normalitási tesztek segítségével.
#Lilliefors (Kolmogorov-Smirnov) teszt
lillie.test(expMintaAtlagok)
#Shapiro-Wilks teszt
shapiro.test(expMintaAtlagok)
#Anderson-Darling teszt
ad.test(expMintaAtlagok)

Már a Lilliefors (Kolmogorov – Smirnov) teszt során kapott ’p-value’ (= 0,04767) is azt mutatja. hogy a nullhipotézist, mely szerint az adatok normál eloszlásúak, 95%-os biztonsággal elvethetjük (noha 99%-os biztonsággal valószínűleg nem). A megbízhatóbb tesztek (Shapiro - Wilks teszt p-value = 9,363*10^-18. és Anderson – Darling teszt p-value = 1,662*10^-5) p-értékei viszont egyértelműen azt mutatják, hogy a mintaátlagok eloszlása NEM normál eloszlású. Ebben az esetben viszont az egymintás Z-próba során alkalmazott törvényszerűségek itt hibához vezetnek. Azon persze ismét csak lehet vitatkozni, hogy ez a hiba mekkora és hogy vajon ez elhanyagolható-e vagy sem. Mindenesetre ajánlatos a minták elemszámának meghatározásakor ezeket a kockázatokat figyelembe venni, hiszen a mintás elemszámának növelésével ez a probléma elkerülhető és akkor egy bizonyos minta elemszám felett már joggal feltételezhetjük majd, hogy a mintaátlagok eloszlása normális.
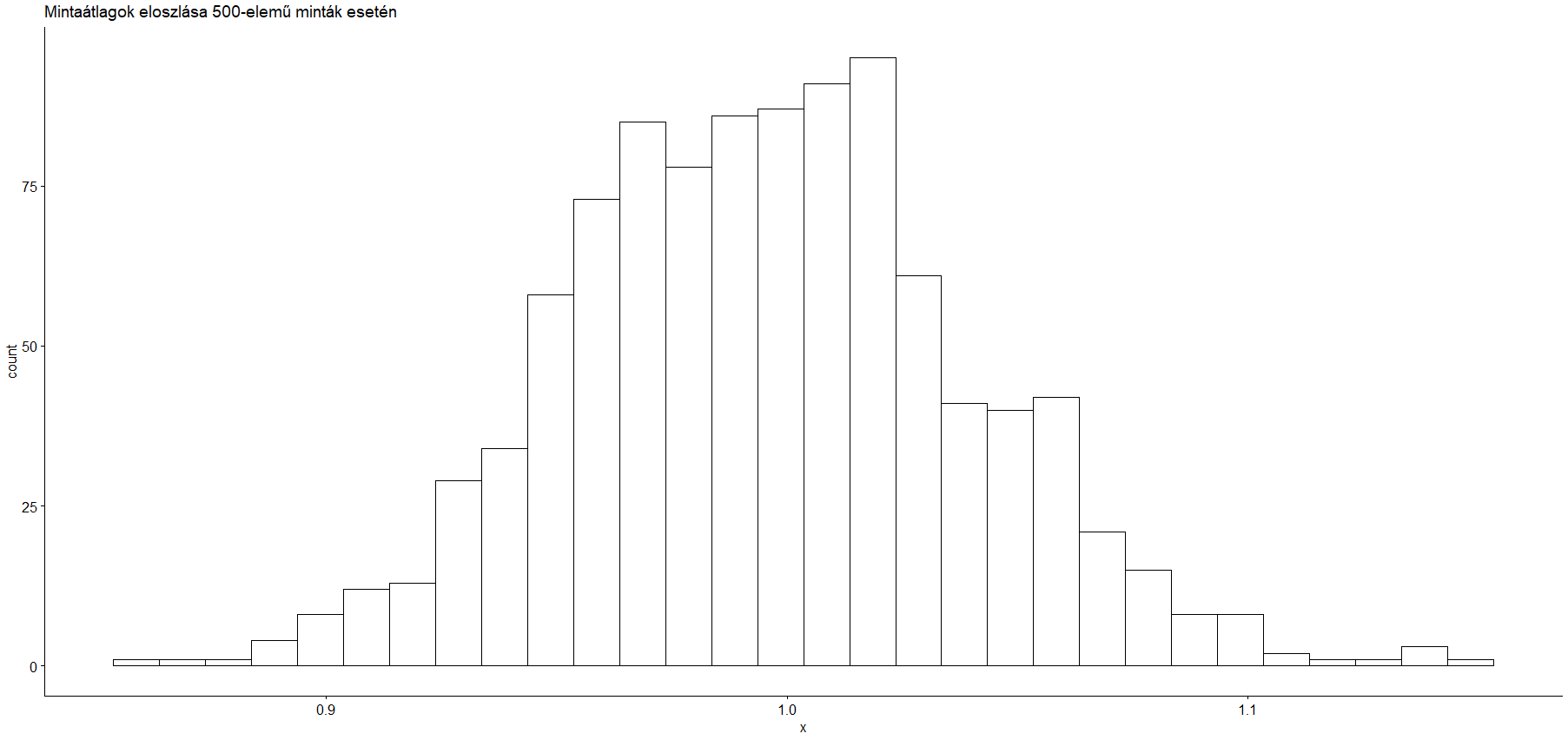

Mondjuk ez esetben 500-elemű mintákat használtam, de ez csak a vizuális hatás kedvéért történt így…





