A kéttényezős varianciaanalízist egy korábbi bejegyzésben (Most nem almára lövünk - kéttényezős varianciaanalízis (Two-way - ANOVA)) már részletesen kiveséztük, így most jöjjön a Minitab változat, amely ismételten sokkal több információt tartalmaz, mint a szimpla táblázatkezelős elemzés – nem véletlen kérnek pénzt is érte. A vizsgálathoz ugyanazt az adatsort fogom használni, hogy az eredmények összevethetők legyenek.
Az egytényezős varianciaanalízis esetében sikerült tisztázni, hogy az tulajdonképpen egy kiterjesztett t-próba, azaz nem kettő, hanem három, négy vagy még annál is több adatsor átlagait hasonlítjuk össze (Emeljük új szintre a t-próbát - az egytényezős varianciaanalízis (One-way ANOVA)). Ez igaz is, de az egytényezős varianciaanalízis a három, négy vagy több adatsort egy megadott tényező szerint csoportosítja, például a sörhab mérési példa esetében (Egy kis sörhabológia – Példa egytényezős varianciaanalízisre (One-way ANOVA)) három különböző rekeszből kivett mintát hasonlítottunk össze. De ugyanígy össze lehet hasonlítani
Rendben, de mi történik akkor, ha egy valamilyen számszerűsíthető értéket nem egy, hanem mondjuk két különböző tényező különféle kategóriáinak hatását szeretnénk felmérni?
Pár hete bemutattam az egytényezős varianciaanalízis lényegét (Emeljük új szintre a t-próbát – az egytényezős varianciaanalízis), illetve kézzel végig számoltunk egy példát is (Egy kis sörhabológia – Példa egytényezős varianciaanalízisre), úgyhogy úgy gondolom, hogy a módszert megfelelő mélységben kiveséztük. Azzal azonban még adós maradtam, hogy hogyan végezhető el a teszt Minitab-ban. Lássuk:
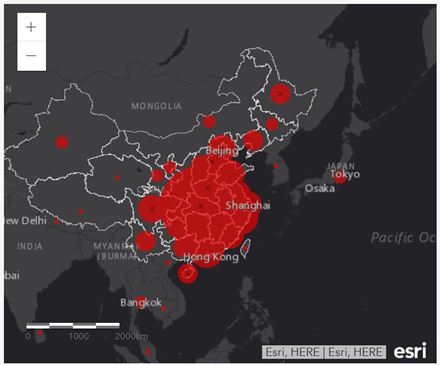
Jelen pillanatban a tavaly decemberben Kínában kitört koronavírus-járvány tartja lázban a világot. Egyelőre senki sem tudja, hogy mekkora lesz a járvány kiterjedése, mennyire gyorsan fog elterjedni a világban, mennyien fognak megbetegedni illetve a betegség miatt meghalni és meddig fog tartani a járvány. Most éppen ott tartunk, hogy a világ szinte minden légitársasága felfüggesztette az összes Kínából és Kínába tartó közvetlen légijáratát 2020 márciusáig. Azért eddig az időpontig, mert a korábbi tapasztalatok (pl.: a 2002-2003-ban kitört SARS járvány lefolyása, mivel az egy hasonló koronavírus volt) alapján erre az időpontra teszik a járvány csúcspontját.
Szerencsére a járványügyi szakemberek nem nézik tétlenül a vírus terjedését, a korábbi hasonló járványok tapasztalatai alapján már léteznek azok a matematikai és statisztikai modellek, amelyek alapján a járvány terjedésének jövőbeni lefolyása – ha nem is jósolható meg pontosan – de becsülhető. A járványok terjedésének modellezésére többféle matematikai modell is alkalmazható, de szinte mindegyik modell az úgynevezett kompartment-, vagy rekeszes modelleken alapul.
1980-ban az NBC-n sugároztak egy dokumentumfilmet „If Japan Can, Why Can’t We?” címmel. Az amerikai autóipart éppen ebben az időben rengették meg a japánból érkező kihívások. A japán autók minősége nagyságrendekkel jobb volt a 70-es években gyártott amerikai autókénál, ráadásul olcsóbbak is voltak. Nemcsak az autók tekintetében, de az acéltermékektől az elektronikáig, a japánok megelőzték az amerikai vállalkozásokat mind a minőség, mind pedig a költségek terén. Az NBC dokumentumfilmje megvizsgálta, hogy ez hogyan történhetett meg. A dokumentumfilm tulajdonképpen annak a magyarázata, hogy egyetlen ember hogyan változtatta meg a japán ipart. Ez az ember egy 80 éves statisztika professzor volt, W. Edward Deming.
Most egy laza balkanyarral elugranék egy teljesen más téma irányába. Eddig az adathalmazok középértékeivel és szóródásával foglalkoztam, de most egy könyv olvasása során felkeltette az érdeklődésemet az extrém szélsőséges események előfordulási valószínűségeinek vizsgálata – legalábbis egy bejegyzés erejéig. Az extrém szélsőséges események – legyenek azok időjárási vagy természeti jelenségek vagy gazdasági események – hajlamosak súlyos következményekkel járni, mert ezekre általában nem vagyunk felkészülve.
Azt hiszem egyetlen sörkedvelőnek sem kell elmagyarázni, hogy egy jó sör élvezeti értékét – sok más tényező mellett – a sörhab különféle jellemzői adják. A mezei sörfogyasztó számára – mint amilyen én is vagyok – a sörhab minősége nem objektív fogalom. Nem tudom megmondani, hogy mitől jó a sör habja, maximum azt tudom eldönteni, hogy az egyik sör habja jobb, mint a másiké. Mivel nem is célom, hogy a tökéletes sörhab készítésének rejtelmeit feszegessem, ha érdekel a témának ez a része, akkor nézd meg ezt a blogbejegyzést:
Ezzel a bejegyzéssel már régóta adós vagyok, hiszen jó ideje foglalkozom már a különféle hipotézis vizsgálatokkal, és a Minitab elemzések bemutatásakor rendszeresen megjelent ez a bizonyos „P-Value”, azaz „P-érték” ami alatt általában egy nulla és egy közötti szám áll. A különféle statisztikai szoftverek helpjében általában csak az van megadva, hogy a különféle tesztek esetében mikor fogadjuk és mikor utasítsuk el a nullhipotézist, de azt szinte sohasem, hogy tulajdonképpen mi is ez. Na, ezen az apró hiányosságon szeretnék segíteni ezzel az írással.
(A dal a képre kattintva indul el)
Vannak megszállottak, akik minden őrültségre képesek azért, hogy megszerettessék másokkal is kedvenc szenvedélyüket. A fent belinkelt dal hallatára valószínűleg senki sem rohan majd a legközelebbi könyvtárba, hogy kivegye az első keze ügyébe kerülő statisztika tankönyvet és nem fog "ráguglizni" a Wilcoxon-féle előjeles rangteszt képletére, de azért érdemes belehallgatni a nótába, amely legalábbis "megmosolyogtató". És azért valljuk be, matematikusoknak is lehet humorérzékük...
Komolyan mondom, így kell adatokat prezentálni! Mintha egy focimeccs közvetítését hallgatnám, miközben a csecsemőhalandóság és a GDP alakulásáról beszél a bácsi. A mozgó grafikák pedig nagyon érthetővé teszik az előadás üzenetét! Kár, hogy csak angol felirat van hozzá... :-(