Pár hete bemutattam az egytényezős varianciaanalízis lényegét (Emeljük új szintre a t-próbát – az egytényezős varianciaanalízis), illetve kézzel végig számoltunk egy példát is (Egy kis sörhabológia – Példa egytényezős varianciaanalízisre), úgyhogy úgy gondolom, hogy a módszert megfelelő mélységben kiveséztük. Azzal azonban még adós maradtam, hogy hogyan végezhető el a teszt Minitab-ban. Lássuk:

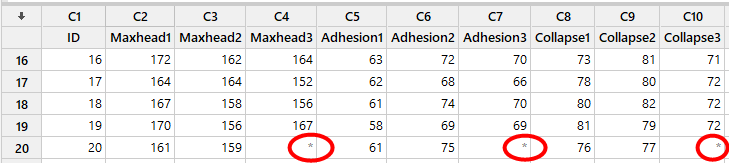
Az adatokat természetesen átmásoltam a táblázatkezelőből a Minitab-ba. Az egyetlen fontos dolog ezzel kapcsolatban az, hogy az egyes ládákhoz tartozó mérési eredmények külön oszlopokban vannak szerepeltetve. Az oszlopok nevében szereplő számok jelzik, hogy melyik oszlop melyik rekeszhez tartozik. A másik megoldás az lenne, ha az összetartozó mérési adatok ugyanazokban az oszlopokban lennének, és egy másik oszlopban lenne jelölve, hogy melyik mérési adat melyik ládához tartozik.

Fontos megjegyzés, hogy az utolsó sorban szereplő – a korábbi bejegyzésben már említett - hiányzó adatot a Minitab egy-egy *-gal jelölte meg.

A Minitab programban az egytényezős varianciaanalízist a Stat menü, ANOVA almenüjében találjuk meg.

A menüpontra kattintva a már megszokott módon megjelenik egy párbeszéd panel.

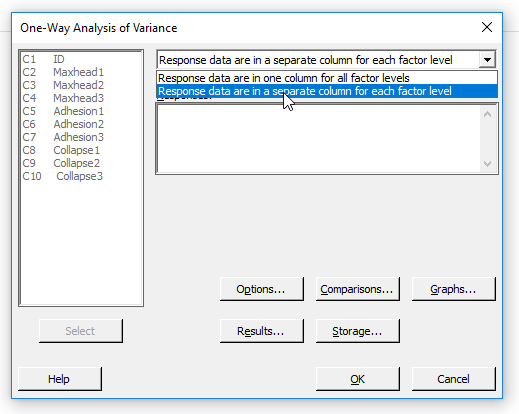
A párbeszéd panel jobb felső részén a már megszokott módon ki tudjuk választani, hogy az adatbázisunkban milyen módon tároljuk az adatainkat. Természetesen ez esetben a második opciót kell kiválasztani, mert a fentebb már említett módon az egyes rekeszekhez tartozó adatokat külön oszlopokban tároltuk el.

Ezután a 'Responses' mezőben meg kell adni, hogy melyik oszlopokat akarjuk használni a vizsgálat során. Jelen esetben a MaxHead1-3 változókat választottuk ki, mert a sörhab maximális magasságának a tulajdonságaira vagyunk kíváncsiak.

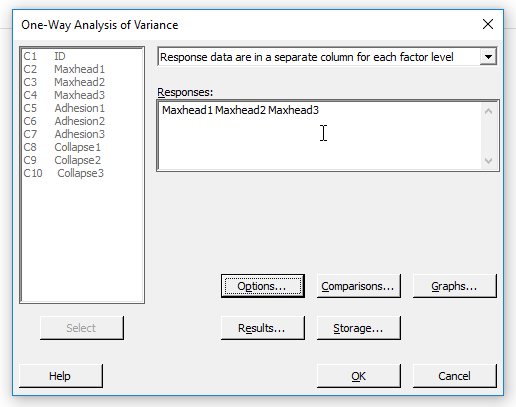
A panel jobb alsó tartományában vannak még gombok, amelyek megnyomásával a teszt további paramétereit tudjuk beállítani. Az ’Options…’ gomb megnyomására megjelenő párbeszéd panelen be lehet állítani a teszt alap paramétereit. Az ’Assume equal variances’ checkbox-t akkor kell bejelölni, ha azt feltételezzük, hogy a különböző adatcsoportok varianciája megegyezik. Ha valami miatt azt feltételezzük, hogy a csoportok varianciája nem egyezik meg, akkor ezt a pipát ki kell vennünk, de akkor viszont nem a korábban ismertetett F-táblázatot fogja használni a szoftver, hanem az úgynevezett Welch tesztet. A Welch’s testről egyelőre legyen elegendő annyi, hogy ez a kétmintás t-próba (Az alkoholfogyasztás hatása a bowling eredményekre – kétmintás t-próba) módosított változata, amit akkor alkalmazunk, ha a minták varianciái között jelentős különbségek vannak. A későbbiekben esetleg visszatérek majd rá, hogy hogyan is működik. A ’Confidence level’, azaz megbízhatósági szint és a ’Type of confidence interval’ azaz a megbízhatósági tartomány típusa már ismerős lehet a korábbi bejegyzésekből (Igaz vagy hamis? – A hipotézis vizsgálatokról…).

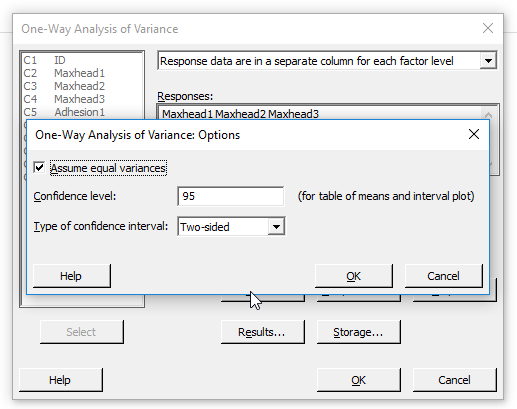
A ’Graphs…’ nyomógomb segítségével ki tudjuk választani, hogy milyen grafikus ábrázolásokat kérünk az eredmények mellé. Beállíthatjuk külön-külön, hogy kérünk-e grafikonokat az adatpontokról, illetve a maradékokról (Hátrébb az agarakkal! – Mennyire hihető a regressziós egyenes becslése?). Az adatpontok esetében felsorolt grafikon típusok már jól ismertek, érdemes kipróbálgatni őket, hogy melyik ábrázolás adja vissza jobban a kapott eredményeket.

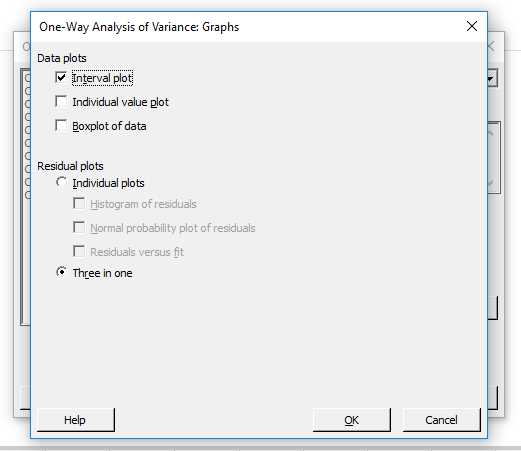
A ’Results…’ nyomógomb segítségével kapott párbeszéd panelen azt tudjuk kiválasztani, hogy milyen eredményeket szeretnénk látni az elemzésekkel kapcsolatban. A ’Display of Results’ legördülő menüben ki tudjuk választani, hogy egyszerű (Simple tables), vagy kiterjesztett táblázatokban (Expanded tables) szeretnénk megkapni az eredményeket. A fenti adatsoron kipróbáltam mindkét beállítást és csak igen kevés különbséget találtam a kétféle ábrázolás között, egyes eredmény táblákhoz hozzáad a Minitab további mezőket. Mivel ezeket nem érzem igazán fontosnak, ezért maradtam az egyszerű tábláknál. A legördülő menü alatt pedig ki tudjuk választani, hogy milyen eredményekre van szükségünk, de ezeken majd a későbbiekben végig megyünk majd.

A ’Storage…’ nyomógomb kiválasztásával azt tudjuk beállítani, hogy a Minitab elmentse-e az illeszkedések (Fits) vagy a maradékok (Residuals) értékeit az egyes adatpontokhoz. Ezt akkor érdemes beállítani, ha ezekkel az adatokkal további elemzéseket szeretnénk elvégezni.

A végére hagytam a legtitokzatosabb nyomógombot, amelyen a ’Comparisons…’ felirat áll. A nyomógombra kattintáskor megjelenő párbeszéd panelen olyan teszteket tudunk kiválasztani, amelyek összehasonlítják az egyes adatcsoportok átlagait, hogy melyik különbözik a többitől. Amint az a korábbiakban már kiderülhetett, az ANOVA táblázatból csak az derül ki, hogy az egyes adatcsoportok között van-e különbség vagy nincs. De ha az F-teszt eredménye az, hogy van különbség a csoportok átlaga között, akkor viszont azt nem mondja meg, hogy melyik csoportok egyformák és melyikek különbözőek. Ennek megállapításához szükség van utólagos vizsgálatokra (post-analysis), hogy megtudjuk, ki lóg ki a sorból. A lentebb felsorolt tesztek (Tukey, Fischer, Dunnett, Hsu MCB) nagyjából mind ugyanazt teszik, kiszámolják az egyes csoportok átlagainak egymáshoz viszonyított távolságát, majd megadnak egy határértéket. Ha a különbség nagyobb a határértéknél, akkor az adott két csoport különbözik egymástól, ha pedig kisebb, akkor az adott két csoport egyforma.

Az előző bekezdésben leírtak miatt először érdemes megnézni, hogy van-e lényeges különbség a három rekesz adatainak varianciája között. Ezért lefuttattam egy leíró statisztikai elemzést az adatokra, csak a szórás helyett a varianciát kérem kiszámoltatni a szoftverrel:

Sajnos a három variancia még csak nem is hasonlít egymásra, így elvileg az F-táblázatot nem lenne szabad használni, illetve nem az adatok összesített varianciájával. Ha ennél is biztosabbak akarunk lenni a dolgunkban, akkor páronként le tudunk futtatni egy tesztet, amit a Minitab úgy nevez, hogy ’Test for equal variances’.

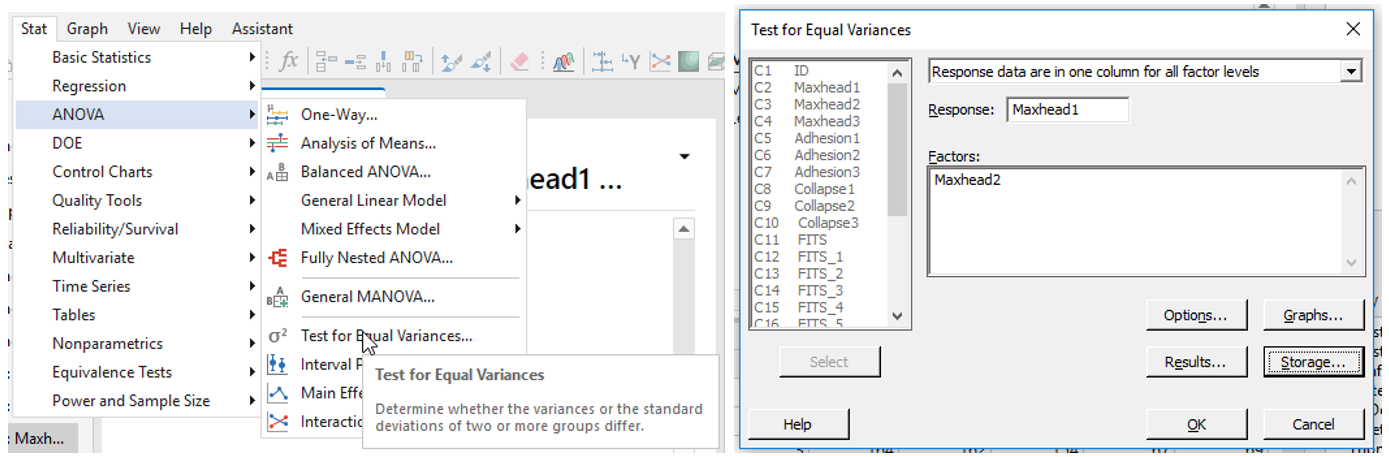
Ez a teszt is azt mutatta, hogy a három adatsor varianciája nem egyezik meg, emiatt úgy döntöttem, hogy elkészítem mindkét módon a tesztet, úgymint az F-táblázatot és a Welch’s próbát is. Először nézzük meg az F-táblázatot.

Az eredmény első része egy összefoglaló a teszt alapbeállításairól. Ez számunkra jól ismert információkat tartalmaz, úgymint a null-, és az alternatív hipotézis, a teszt megbízhatósági szintje, illetve fel lett tüntetve még két információ. Az egyik, hogy van egy nem használt sor az adathalmazunkban, ez valószínűleg az utolsó sor lesz, ahol a harmadik rekesz nem 20 hanem csak 19 sorból áll. A cikk elején említettem, hogy a hiányzó értékeket a Minitab *-gal helyettesítette. A ’Factor information’ ismét csak azt jelzi, hogy mely oszlopokat használtuk fel a teszthez, szóval ez sem tartalmaz lényegi új információt.

A harmadik szakasz az F-táblázat, vagy ANOVA-táblázat, amely a tesztünk végeredményét tartalmazza:

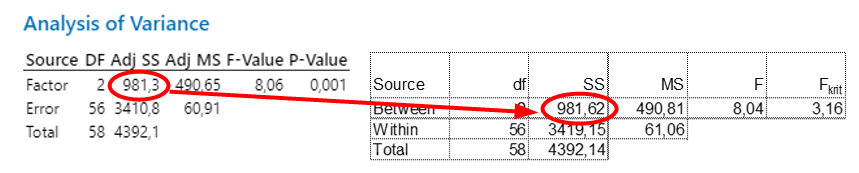
Az összehasonlítás kedvéért idemásoltam az előző bejegyzésben kijött végeredményt. Az adatok nagyságrendileg megegyeznek, de azért vannak kisebb-nagyobb különbségek (természetesen kivéve a végét, mert a Minitab kiszámolta a P-értéket, én viszont az Fkritikus értékkel számoltam. Viszont azt hozzátenném, hogy a táblázatkezelőben nem egy közös varianciával számoltam, hanem az egyes oszlopok varianciáival külön-külön. Sajnos a Minitab nem is enged F-táblázatot kiszámolni, ha a varianciák nem egyeznek meg, így közvetlenül nem tudom összehasonlítani, hogy vajon a Minitab és a táblázatkezelő ugyanazt az eredményt hozza-e ki, de feltételezem, hogy igen. Mindezek ellenére az eredmény ugyanaz mindkét esetben, elvetjük a nullhipotézist és az alternatív hipotézist fogadjuk el.

A következő blokk az úgynevezett ’Model Summary’, amely a regresszióelemzéshez hasonlóan megadja, hogy a modell mennyire takarja le a valóságos adatokat. Hát ez elég vacak! A táblázatban szereplő ’S’ az adatsor összesített szórása, az ’R-sq’, az ’R-sq(adj)’ és az ’R-sq(pred)’ pedig összehasonlítja az adatsor valós szóródását az elméleti szóródásával. A pontos definíciók ebben a cikkben találhatók (Hátrébb az agarakkal! – Mennyire hihető a regressziós egyenes becslése?). Ezeknek 70% felett kellene lenniük, viszont a legnagyobb is csak 19,57%. Ez azt jelzi, hogy ez a modell így nem igazán passzol az adatsorunkhoz, tehát érdemes fenntartásokkal kezelni az eredményeket (ami az eltérő varianciák miatt akár még érthető is.

A következő szekcióban a Minitab kiszámította az egyes rekeszek adatainak átlagait, illetve ezek megbízhatósági tartományát, vagyis azt, hogy az adott mintákat reprezentáló sokaságok átlagai milyen tartományban vannak. Ez a táblázat segít nekünk abban, hogy össze tudjuk hasonlítani az egyes rekeszek adatait, hogy melyikek lehetnek egyformák és melyikek különböznek.

A ’95% CI’ azaz a 95%-os megbízhatósági tartományok összehasonlítása azt az eredményt mutatja, hogy a ’Maxhead1’ megbízhatósági tartománya jelentősen nagyobb, mint a ’Maxhead3’-é és a ’Maxhead2’ megbízhatósági tartományával is csak egy leheletnyi átfedést mutat (163,70 <> 163,996). A ’Maxhead2’ és a ’Maxhead3’ adatsorok megbízhatósági tartományai viszont átfedik egymást.

Mivel az ANOVA alapján az alternatív hipotézist kellett elfogadnunk, ezért még szükségünk van további vizsgálatokra annak érdekében, hogy vajon melyik adatsorok egyeznek meg és melyikek különböznek. Ezért a teszt indítása előtt beállítottam, hogy futassa le a program a Tukey-tesztet (Taki-teszt) is.

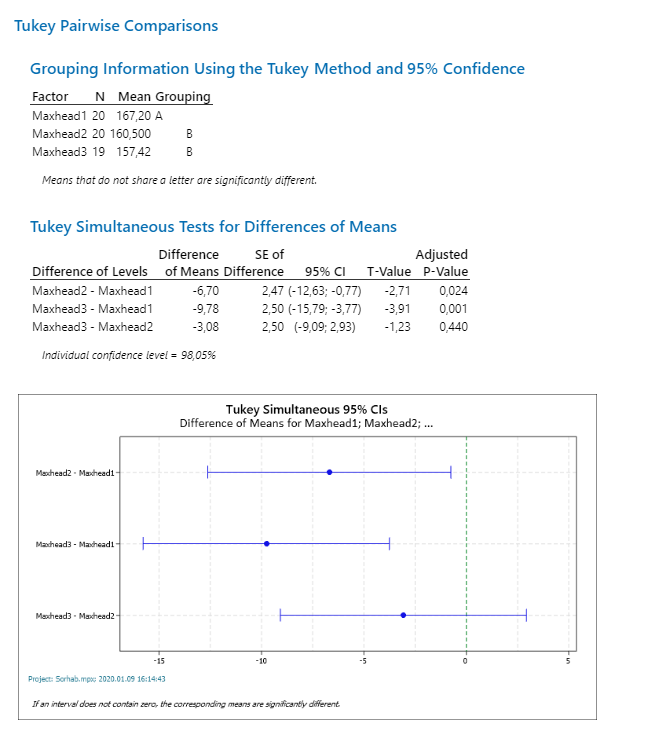
A Tukey-test végrehajtásakor a program először csoportokba rendezte az egyes oszlopok értékeit úgy, hogy a végén kijöjjön, hogy melyik adatsorokat lehet egy csoportba vonni. Ezt mutatja a ’Grouping Information Using the Tukey Method and 95% Confidence’ blokk végén a ’Grouping’ oszlop, ahol a ’Maxhead1’ lett az ’A’ csoport a ’Maxhead2’ és a Maxhead3’ pedig a ’B’ csoport. A blokk aljára az van odaírva dőlt betükkel, hogy amelyik csoportok között nincs átfedés a betükben, azok külön csoportba sorolandók. A ’Tukey Simultaneous Tests for Differences of Means’ szekció pedig az egyes csoportok átlagainak különbségeit elemzi. A csoportok minden kombinációjára elvégez egy kétmintás t-próbát, majd a táblázat végén szereplő ’Adjusted P-Value’ értéke megadja, hogy melyik csoportok lehetnek egyformák és melyikek nem. Itt is kijön ugyanaz, hogy a Maxhead1 – Maxhead2’ és a ’Maxhead1 – Maxhead3’ esetében az ’Adjusted P-Value’ értékei kisebbek 0,05-nél, azaz ezeknél a kétmintás t-próbák nullhipotéziseit elutasítjuk, a ’Maxhead2 – Maxhead3’ esetében viszont az ’Adjusted P-Value’ értéke 0,44. Emiatt ebben az esetben elfogadjuk a nullhipotézist, azaz a két adatsor átlaga megegyezhet.

A diagramon pedig a párok átlagkülönbségeinek megbízhatósági intervallumai láthatók, illetve egy szaggatott vonal a 0-nál. Az első két esetben a kék vonalak nem keresztezik a 0-vonalat, a harmadik esetében pedig igen. Ha egy megbízhatósági tartomány (95% CI) nem metszi a 0-vonalat, az azt jelenti, hogy a két átlag különbsége nem lehet 0, azaz a két átlag nem egyezhet meg a megadott megbízhatósági szinten. Ellenkező esetben viszont igen.

Ezután már csak két diagram szerepel a jelentésben. Az egyik egy wishkers-plot, amely a három minta egymáshoz képesti elhelyezkedését mutatja, illetve a maradékok elemzéseinek diagramjai.

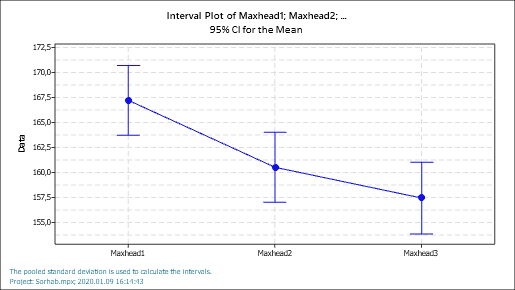
Ez a diagram gyakorlatilag vizuálisan ábrázolja a ’Means’ blokkban található számszerű értékeket.

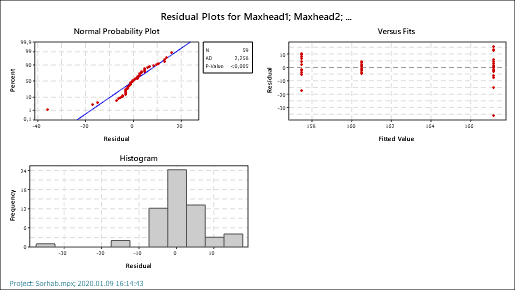
A maradékok elemzése azt mutatja, hogy a három adatsor nem teljesen normál eloszlású, a baloldalon található ’Normal Probability Plot’-on és ’Histogram’-on látszik 3 pont, amelyek elviszont az adatsort. A jobboldali diagramon (Versus Fits) az látszik, hogy a kieső értékek elsősorban a ’Maxhead1’-et és a ’Maxhead3’-at büntetik, a ’Maxhead2’ szórása egészen kicsi a másik kettőhöz képest.

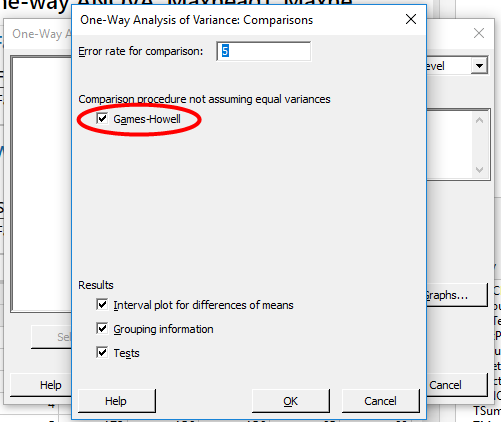
A másik feladat az volt, hogy lefuttassam a tesztet úgy is, ha azt feltételezem, hogy a három adatsor varianciája NEM EGYEZIK MEG. Amint azt már fentebb említettem, ekkor a szoftver nem hajlandó ANOVA-táblázatot készíteni, hanem az úgynevezett Welch’s-próbát végzi el. A korábbiakhoz képest csak néhány különbséget lehet találni a kapott jelentésben. Már a megjelenő párbeszéd paneleken más információ jelenik meg. Ha az ’Assume equal variances’ mezőből kivesszük a pipát, akkor…

… a ’Comparisons…’ párbeszédpanelen csak egy összehasonlító teszt fog megjelenni.

Az eredmények terén is vannak eltérések:

Az első, hogy itt nincs ANOVA-táblázat, helyette egy ’Welch’s Test’ nevezetű táblázat jelenik meg.

A Welch’s test ugyanazt az eredményt hozta, mint az ANOVA-táblázat, azaz elvetjük a nullhipotézist és az ellenhipotézist fogadjuk el, vagyis a három adatsor átlaga nem egyzik meg, a három rekesz körül legalább az egyiknek az átlaga különbözik. Sajnos a ’Model Summary’ itt sem hozott kedvezőbb értékeket az r-squared különféle változatai itt is 13 és 19% között mozognak.

Természetesen a páros összehasonlítás során a fentebb említett Games-Howell tesztet láthatjuk, de az eredmények nagyon hasonlítanak Tukey-teszthez, csak a számítás módja különbözik egy kicsit.

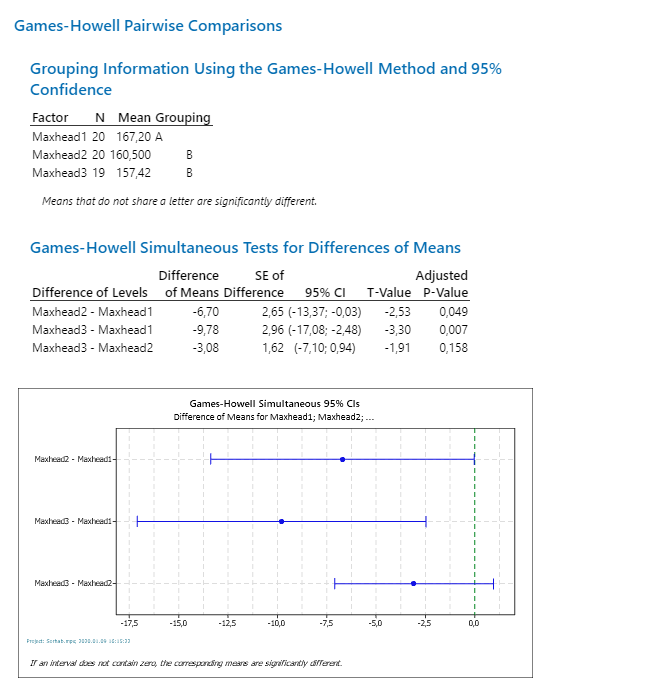Az utolsó különbség az ’Interval Plot’ nem egyformának mutatja az egyes rekeszek adatainak szóródását, hanem különbözőnek.

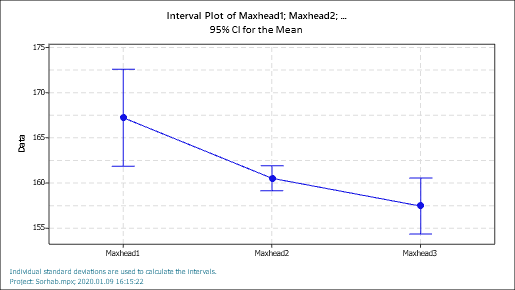
Összefoglalás: A vizsgálat egy kicsit hosszadalmasra sikeredett, mert a Minitab értelemszerűen sokkal több beállításra és addícionális vizsgálatra ad lehetőséget szemben a táblázatkezelővel. Mivel a Minitab szinte végig vezet a vizsgálatokon, ezért már itt sok hasznos információval lettünk gazdagabbak arról, hogy milyen helyzetekben miket kell megvizsgálnunk a felhasznált adatsorokkal kapcsolatban. A Minitab elemzése talán bonyolutabbnak tűnik, viszont az elemzés gyakorlott kézzel sokkal rövidebb ideig tart, mint a táblázatkezelővel végig számolni a teszteket.