Az előző bejegyzésben (Tudom, hogy gőzgép, de mi hajtja? – Egyváltozós lineáris regresszió – a regressziós egyenes meghatározása) végül sikerült meghatározni az x és az y változók kapcsolatát leíró egyenes egyenletét. Ennek örömére persze pezsgőt lehetne bontani, de sajnos a feladat itt még nem ért véget, sőt a munka oroszlánrészét még ezután kell elvégezni. A probléma az, hogy hiába határoztuk meg a keresett függvényképletet, semmilyen garancia sincs arra, hogy az adott x-értékhez az egyenlet segítségével meghatározott ŷ érték a valóságban is annyi lesz.

A papír és a monitor mindent elbír, de a mindennapi gyakorlatban csak akkor van értelme használni a függvény képletét, ha az általa meghatározott „jóslat” relatíve nagy pontossággal megvalósul a gyakorlatban, vagyis a „jósnő üveggömbje” megbízhatóan működik. A képletünk „jóságáról” nem tudunk egy mozdulattal vagy egyetlen képlet alkalmazásával meggyőződni, ez nem egy nagyon konkrét igen-nem-talán típusú döntés, hanem többféle tesztet kell kiszámolni és többféle grafikont kell megrajzolni és értelmezni ahhoz, hogy a képletünk esetleges hibáit felfedezzük. A végén persze el kell jutnunk egy valamiféle értékítélethez arról, hogy mennyire bízunk meg a képlet által adott eredményekben, de ez egy komplex döntési mechanizmus eredménye.

Először is van néhány olyan képlet, amelynek segítségével képet kaphatunk arról, hogy a függvényképlet „hány százalékban” írja le a valóságot. Ezek az ellenőrző képletek szintén becslések, tehát irányt mutatnak, de nem feltétlenül kell szó szerint venni őket. Az egyik ilyen mérőszám az R-négyzet (R-sq), amelyet szimplán a korrelációs együttható négyzetének is szoktak nevezni, de szerintem ez lehet, hogy igaz, de félrevezető. Úgy gondolom, hogy ez esetben is érdemes az eredeti filozófiának megfelelő formát alkalmazni:

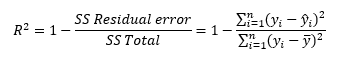
Ez így most megint csak nehezen érthető, ha nem olvastad a kettővel ezelőtti bejegyzésemet a legkisebb négyzetek módszeréről (Legyenek a négyzetek minél kisebbek…! – útban a lineáris regresszió elemzés felé). Ebben a másik bejegyzésben már ismertettem a fenti képletben szereplő tört számlálójának és nevezőjének a jelentését is, de azért – ismétlésképpen – nézzük, hogy melyik mit jelent. Az első képletben szereplő SS a Sum of Squares, azaz „Négyzetek Összege” kifejezés rövidítése. A „Residual error” azaz a maradékok hibája kifejezés a pontok távolságát jelenti az elméleti egyenestől, a „Total” azaz „Összes” kifejezés a pontok távolságát jelöli az y változó átlagától, ahogyan az a jobboldali grafikonon látható. Hogy a zűrzavart tovább fokozzam, ezt a jellemzőt „maradék”-nak vagy „residual”-nak is szokták hívni.

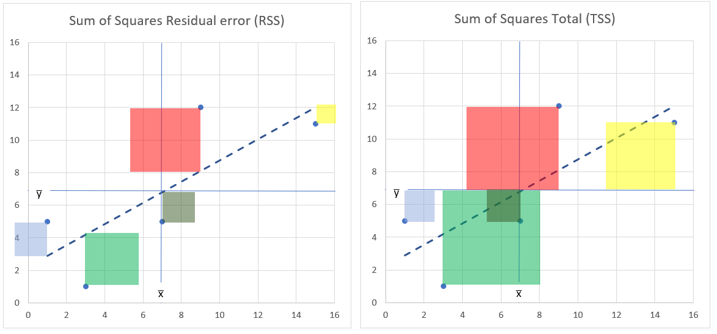
Az ábrákon a Sum of Squares, azaz a „Négyzetek Összege” jelentése látható a tört számlálója és nevezője esetében. Mit is jelent ez a képlet a fentiek alapján. Az biztos, hogy minél közelebb vannak a pontok az elméleti egyeneshez, azaz minél kisebb a „hiba” szórása, annál kisebb lesz a tört értéke, hiszen az SS Error a tört számlálójában van. A nevezőben a pontok teljes y-irányú szórása szerepel. Mivel az elméleti egyenes egyenletének hibáját teljes mértékben y-irányban vizsgáljuk, ezért logikusnak tűnik a hibát a teljes y-irányú szóráshoz viszonyítani, ha egy százalékos eredményt szeretnénk kapni. A tört értékét – szerintem – azért vonjuk ki 1-ből, hogy százalékosan akkor mutasson a képlet magasabb százalékos eredményt, ha a tört értéke kisebb, azaz a pontok hibája az elméleti egyeneshez képest minél kisebb. Így, ha a pontok tökéletesen illeszkednek az elméleti egyenesre, akkor R² értéke 100% lesz (azaz 1 – 0 = 1), és minél távolabb vannak a pontok az egyenestől, annál nagyobb lesz a tört értéke, azaz annál kisebb lesz R² értéke. Ez egy használható mérőszám az elméleti egyenes egyenletének „jóságát” megítélni, de a komoly statisztikusok úgy tartják, hogy a többváltozós lineáris regresszió elemzés esetében ez a mérőszám arra készteti a lelkes elemzőt, hogy növelje a befolyásoló tényezők számát az R² értékének növelése érdekében, mert minden egyes újabb változó bevezetésekor nőni fog az R² értéke, ami téves következtetésekhez vezethet. Maradjunk annyiban, hogy ezt még nem értjük, de ennek következményeképpen bevezetésre került egy újabb mérőszám, amelyet módosított R²-nek (Adjusted R-sq vagy Adj-R-sq) neveznek. Ez csak annyiban különbözik az R² eredeti képletétől, hogy a nevezőben a teljes y-irányú szórást még el kell osztani a szabadsági fokok számával, amely annál nagyobb, minél több független változó hatását vizsgáljuk.

A fenti képlet csak kétváltozós elemzés esetében igaz, ha több x változó alkalmazásával akarjuk becsülni az egyenesünk képletét, akkor n-ből, amely a vizsgált ponthalmaz elemeinek számát jelzi, a vizsgált x-változók + a konstans számát kell kivonni, azaz x1 és x2 + konstans esetében 3-t, x1, x2, x3 és konstans esetében 4-et és így tovább. Egyébként ennek az a következménye, hogy egyváltozós regresszió elemzés esetében a kétféle R² értéke közel azonos, de minél több x-változót vezetünk be, annál nagyobb lesz az eltérés a kétféle mérőszám között és annál inkább figyelembe kell vennünk a módosított R² értékét a döntésben.

Van egy harmadik mérőszámunk is, amely nem annyira az elméleti egyenes illeszkedését vizsgálja a ponthalmazra, hanem az egyenes „előrejelzési képességét”. Ezt a mérőszámot „Becsült” R²-nek (Predictive R-sq vagy Pred R-sq) nevezik és azt vizsgálja, hogy ha a ponthalmaz valamelyik pontja eltávolításra kerül a ponthalmazból, az mennyiben befolyásolja az elméleti egyenes képletét. A „Becsült” R² eredménye egy mátrix művelet, amit most nem szeretnék levezetni, de a Minitab ismeri ennek kiszámítási módját, vagyis most fogadjuk el, hogy ezt „csak” értelmezni kell. Ha a „Becsült” R² sokkal kisebb, mint a sima R², az mindig problémát jelez, valószínűleg túl sok az x-változó, amellyel becsülni akarjuk a modellt. Viszont ez a probléma is csak a többváltozós regresszió elemzésnél jön elő, amellyel most nem foglalkozunk, csak azért írtam le, hogy érthető legyen, amit egy szoftver megjelenít eredményként.

Bár nem nagyon lehet arról olvasni, hogy mekkora legyen R² értéke ahhoz, hogy elfogadjuk a modellt, én azt mondanám, hogy 70% feletti R² már egészen jónak számít, szerintem az R² eredményét 70% felett már el lehet fogadni. Persze ez még nem jelenti azt, hogy a regressziós egyenes elég jó, csak azt, hogy az R² értéke jó.

A második feladat a modellünk pontosságának ellenőrzésére, ha kiszámoljuk a pontoknak az elméleti egyenes körüli varianciáját (MS Error vagy S²), amely a fent tárgyalt SS Error-ral szemben nem a pontok és az elméleti egyenes közé rajzolt négyzetek összege, hanem az átlaga:

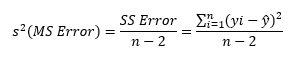S² alkalmazásának legpraktikusabb módja, ha az elméleti egyenes alá és fölé odarajzoljuk a tőle 2 x S² távolságra lévő megbízhatósági határokat. Az elméleti egyenes egyenletét akkor fogadjuk el megfelelőnek, ha a pontok 90%-a benne van a megbízhatósági határok által kijelölt tartományban. Ez így egy sokkal látványosabb. mint az R² mérőszámok alkalmazása. A lenti baloldali grafikonon ugyanennek a módszernek a szofisztikáltabb változata látható, amikor konkrétan kiszámítjuk (vagy a Minitab kiszámítja) a 95% megbízhatósági intervallumokat és ez alapján tudjuk meghozni ugyanezt a döntést.

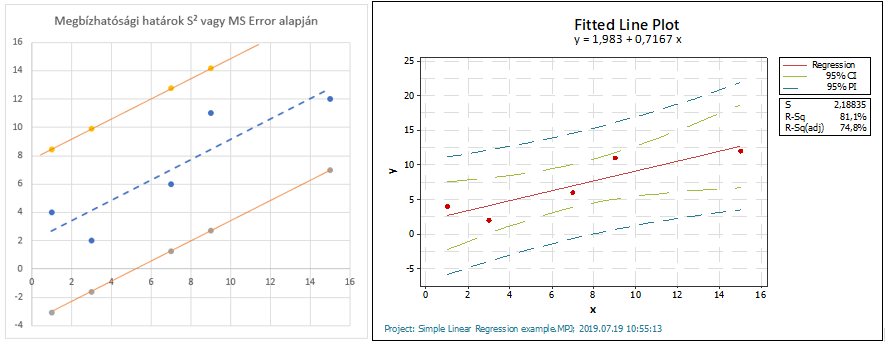
A harmadik vizsgálat, amit nagyon ajánlott elvégezni, az a maradékok, azaz a „residual”, azaz az MS error részletes grafikai vizsgálata. Ezeknek a maradékoknak van néhány olyan tulajdonsága, amelyeket mindenképpen meg kell vizsgálni a modell megfelelősége szempontjából:

• A maradékok eloszlása legyen normál eloszlás
• A maradékok egyenletesen szóródjanak a 0 vonal alatt és felett, ne legyen látható semmilyen szabályos mintázat
• A maradékokat sorba rendezve se legyen látható semmilyen a véletlenszerűtől eltérő mintázat

A Minitab például egy ehhez hasonló összefoglaló grafikus riportot készít a maradékok elemzéséhez:

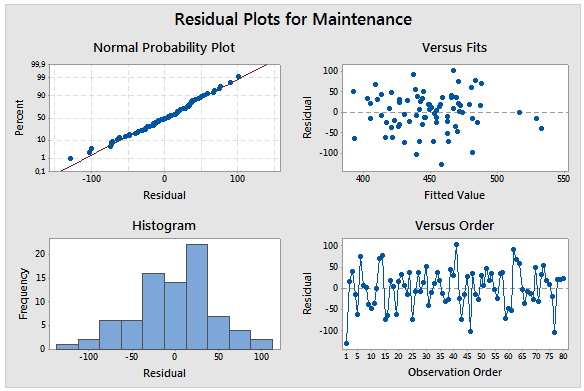
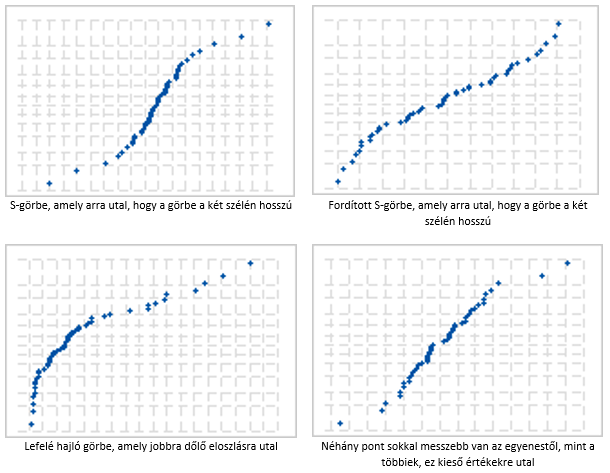
Az ábrán négy grafikon látható. A jobboldali grafikonok a maradékok (Residuals) normál eloszlását vizsgálja. A normal probability plot (normál eloszlás diagram) esetében azt kell látnunk, hogy a pontok szépen ráfekszenek az egyenesre a Q-Q diagramon. Milyen hibák fordulhatnak elő a Q-Q diagramon:

A hisztogramon egy a normál eloszlás haranggörbéjére emlékeztető formát kell látnunk. Az én példámban ehhez nagyon kevés az az 5 darab pont, amelyet vizsgálok, de elegendően nagyszámú minta esetében a hisztogram is tud hasznos információkkal szolgálni. Itt is megjelenhet a görbe aszimetriája, az, ha a görbe túl magas vagy túl lapos, vagy ha kieső értékek vannak a maradékok között.

A maradékok szóródását, illetve a véletlenszerűtől eltérő viselkedését a két jobboldali diagramon lehet észlelni. A jobb felső diagram az úgynevezett „Residual versus fit” diagram tulajdonképpen annyit tesz, hogy az elméleti illeszkedő egyenest vízszintesen ábrázolja és azt tekinti nullának, a pontok pedig az adathalmaz pontjainak y-irányú távolságát jelzi a „nulla” egyenestől. Akkor jó a kép, amit látunk, ha a pontok nagyjából egyenletesen oszlanak el az egyenes mentén, azaz

• körülbelül ugyanannyi pont van az egyenes alatt, mint felette,
• körülbelül ugyanannyi pont van a diagram baloldalán, közepén és jobboldalán is
• a pontok szóródása az egyenes körül megegyezik a diagram baloldalán, közepén és jobboldalán is
• A pontok sűrűsége is egyenletes a diagram egész területén, nincsenek olyan helyek, ahol a pontok sűrűbben vagy ritkábban helyezkednek el, mint máshol
• Nincsenek kieső értékek, amelyek jelentősen nagyobbak a többinél

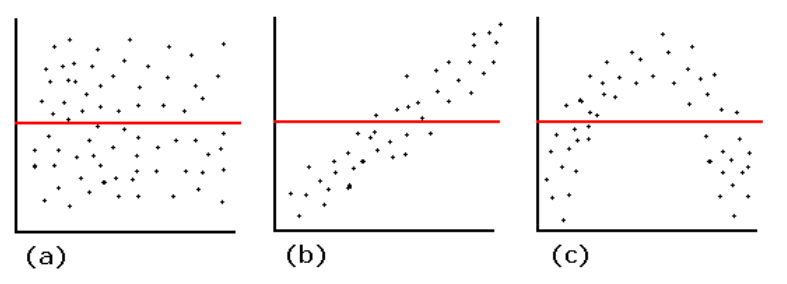
A teljesség igénye nélkül legyen itt egy példa arra, hogy mit kell látnunk és mit nem szabad egy „residulas versus fits” diagramon. Természetesen az (a) ábra egy egyenletes eloszlású képet mutat, ebben az esetben elfogadhatjuk a maradékok eloszlását. A (b) és a (c) esetben a maradékok eloszlása nem egyenletes és nem véletlenszerű, szabályos mintázatot követ.

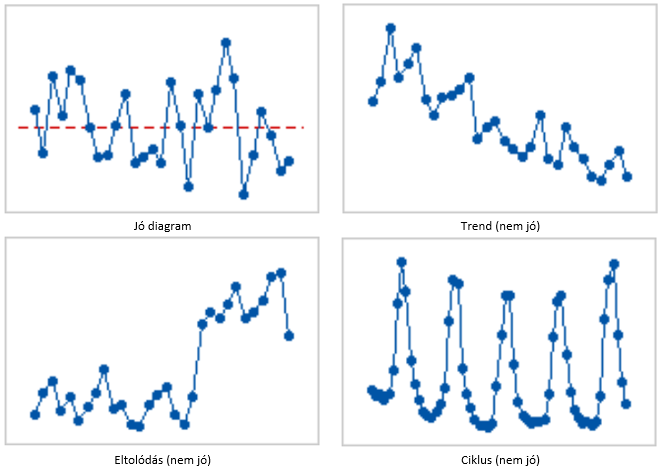
A jobb alsó diagram pedig a „Residuals versus order” nevet viseli büszkén, amely annyit tesz, hogy ezen a diagramon a maradékok a „keletkezés sorrendjében” vannak ábrázolva. Így például felfedezhetők az adatgyűjtéssel és / vagy az adatok bevitelével kapcsolatos hibák, vagy szabályosságok. Az elfogadhatóság feltétele itt is a pontok egyenletes eloszlása és a „véletlenszerűség”, hasonlóan a „Residuals versus fits” diagramhoz. Kerüljön itt is bemutatásra egy jó diagram és néhány jellegzetes hiba:

Összefoglalásul vegyük még egyszer végig, hogy milyen ellenőrző teszteket érdemes elvégezni a regressziós egyenes használhatóságának ellenőrzésére:

• R² (R-sq), módosított R² (Adj R-sq) és becsült R² (Predicted R-sq) kiszámítása. 70% feletti értékek kívánatosak.
• S² kiszámítása és a megbízhatósági intervallum berajzolása a regressziós egyenes alá és fölé. A pontok 90%-a legyen a megbízhatósági tartományban.
• A maradékok, azaz a Residuals grafikus vizsgálata. Az elfogadhatóság feltétele ez esetben az, hogy a grafikus elemzés során ne találjunk semmilyen jelét annak, hogy a maradékok nem véletlenszerűen viselkednek.

Természetesen vannak még további ellenőrző tesztek, amelyeket még be lehetne mutatni, de a fent felsoroltak a legegyszerűbbek és a legkönnyebben érthetőek. A Minitab által generált standard riportban is vannak olyan elemek, amelyeket itt nem magyaráztam el, ezekre még a későbbiekben sort fogok keríteni.