Korábban már tárgyaltam a normál eloszlás mögött húzódó filozófiát (lásd itt és itt), szóval itt az ideje, hogy összefoglaljam a normál eloszlás legfontosabb tulajdonságait, legalábbis azokat, amelyek a gyakorlati alkalmazás szempontjából fontosak.

Amint az már a korábbi bejegyzésekben kiderült, a normál eloszlás sűrűségfüggvénye egy szimmetrikus harang alakú görbe, amely az adatok (legyen az egy sokaság vagy egy minta) átlaga körül rajzolódik ki. Egészen konkrétan a haranggörbe legmagasabb pontja megegyezik az adatok átlagával, amely megegyezik az adatok mediánjával és móduszával is. Ez egyben azt is jelenti, hogy az adatok e pont körül helyezkednek el a legsűrűbben. Minél távolabb van a vizsgált pont az átlagtól az x-tengely mentén, annál ritkábban fordulnak elő olyan értékek, amelyek pont ekkora távolságra vannak az átlagtól.

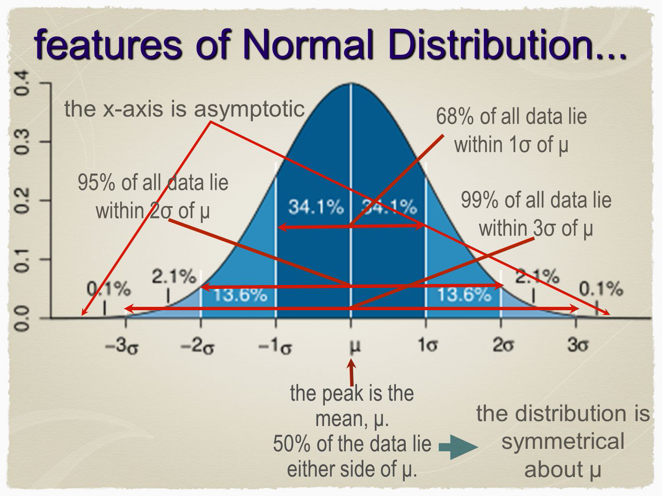
A sűrűségfüggvény görbe alakja nagymértékben függ az adatok szórásától. Ez olyannyira igaz, hogy az adathalmaz szórásának plusz-mínusz egyszeres, kétszeres, háromszoros vagy négyszeres értékei által kijelölt tartományok kiemelten vannak kezelve. A következő ábrán az x-tengelyen az adatok szórásának fent megjelölt plusz-mínusz egyszeres, kétszeres, háromszoros és négyszeres értékei által kijelölt tartományok láthatók, az y tengelyen pedig egy adott x-értéket felvevő adatok gyakorisága látható.

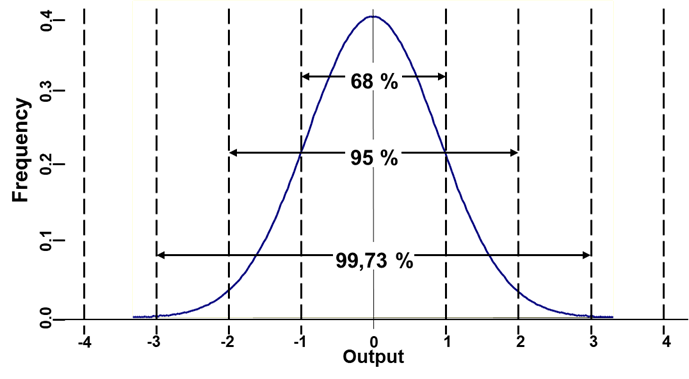
A sűrűségfüggvénygörbe lehet laposabb vagy magasabb, illetve szélesebb vagy karcsúbb, az adatoknak mindig körülbelül ugyanakkora százaléka lesz benne a fent megadott tartományokban. Ezek a százalékos arányok a normál eloszlás függvénybe a nevezetes szórástartományok szélső értékeit behelyettesítve egyszerűen kiszámíthatók.

A haranggörbe két vége sohasem fogja elérni az x-tengelyt, azaz a nullát, ahogy x értékei tartanak a plusz végtelen, illetve a mínusz végtelen felé, úgy fognak a gyakorisági értékek tartani a nulla felé. Ez egy kicsit filozófiai megközelítésben azt jelenti, hogy elméletileg nincs olyan esemény, amelynek nulla lenne a valószínűsége, csak olyan, amely eszméletlenül kicsi.

- Mivel a sűrűségfüggvény görbe egy teljes eseményteret fed le, ezért a függvénygörbe alatti terület nagysága mindig 1. Ez azt jelenti, hogy ha meghatározzuk annak a valószínűségét, hogy x egy adott értéket, vagy annál nagyobb értéket vesz fel, azt úgy is megtehetjük, hogy meghatározzuk azt, hogy mekkora a valószínűsége annak, hogy x az adott értéket vagy annál nagyobbat vesz fel, majd ezt a valószínűséget kivonjuk 1-ből.

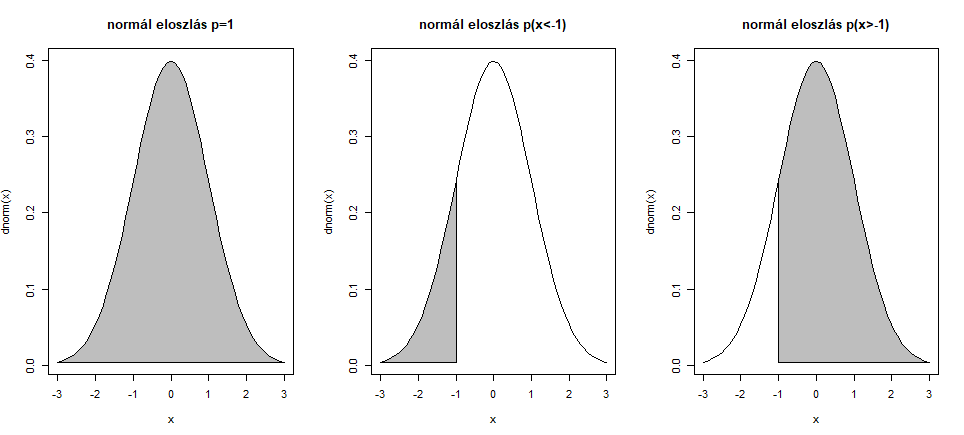
Mivel a sűrűségfüggvény görbe szimmetrikus, annak több következménye is van.

- Az átlag alatti és az átlag feletti terület nagysága egyenlő, azaz annak a valószínűsége, hogy x értéke az átlagnál kisebb, az 50% ugyanúgy, mint annak, ha x értéke az átlagnál nagyobb.

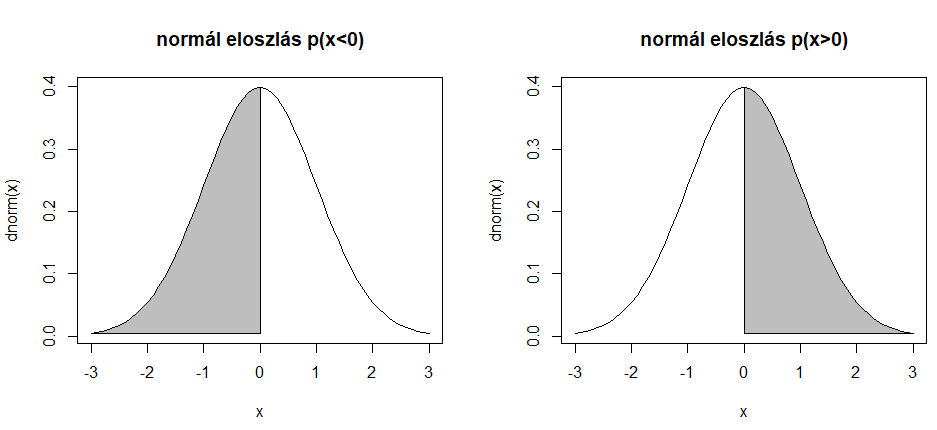
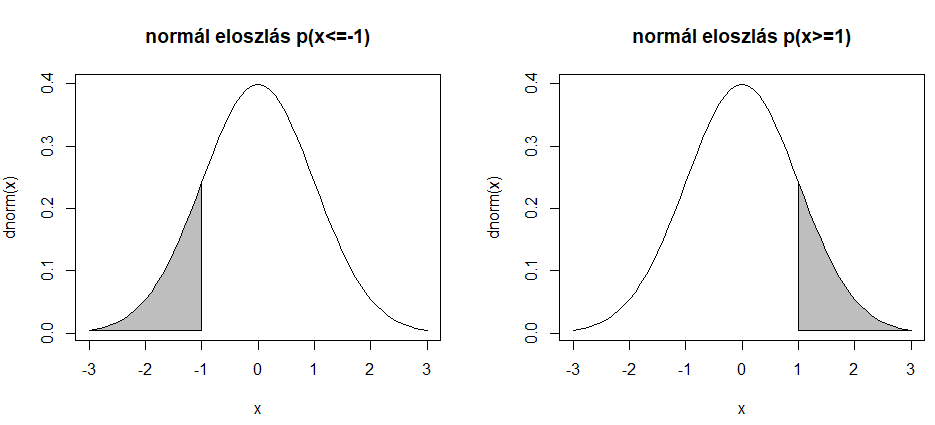
Annak a valószínűsége, hogy x értéke például 1 vagy annál nagyobb, az ugyanakkora, mintha x értéke -1 vagy annál kisebb lenne.