Az előző cikk alapján (Z, mint Z-próba…Egymintás!) tulajdonképpen papíron is egyszerűen végig lehet számolni a feladatot. Amennyiben valaki rendszeresen használja ezt a tesztet (ami nem túl gyakori), vagy szeretne több értékkel eljátszani, viszont nincs pénze vagy lehetősége statisztikai szoftvert használni, az akár egy táblázatkezelőben is el tud készíteni egy olyan lapot, amely a kezdő adatok megadása után automatikusan elvégzi a számításokat és kiértékeli az eredményeket.

A fent látható táblázat akár jegyzőkönyvként is alkalmazható és bár nem teljesen automatikus, azért tartalmaz néhány apró kényelmi funkciót, azonban nincs túlbonyolítva. A teszt táblázat felépítése a következő:

1. A feladat megfogalmazása
   Mielőtt belekezdünk a tesztbe, először is el kell döntenünk egy pár dolgot például, hogy miről szól a teszt, mi a nullhipotézis és az ellenhipotézis, mi a teszt típusa, azaz egyoldali vagy kétoldali tesztről van szó, illetve egyoldali teszt esetén arra számítunk, hogy a minta átlaga kisebb lesz, mint a sokaság átlaga vagy nagyobb. El kell még döntenünk azt, hogy milyen megbízhatósági szinten szeretnénk vizsgálni a kérdést. A későbbiekben látni fogjuk, hogy a tábla tulajdonképpen az összes esetet kiszámolja, de érdemes már az elején döntést hozni azért, hogy a teszt eredményeinek ismerete ne befolyásolja a döntésünket. A teszt típusát és a megbízhatósági szintet legördülő beviteli mező segítségével lehet kiválasztani.
2. A minta elemei
   Ha megvannak konkrétan a minták adatai, akkor ezeket be lehet gépelni a bal oldalon található sárga oszlop mezőibe. Ha itt vannak adatok, akkor a minta átlagát és elemeinek számát automatikusan kiszámolja a tábla. Ha nem akarunk ezzel foglalkozni, akkor a minta bemenő adatainál közvetlenül is be lehet gépelni az adatokat, csak ekkor a képletek felülíródnak. Jelen esetben csak 25 adatnak biztosítottam helyet, de ez nagyon egyszerűen bővíthető, csak a minta bemenő adatainak képleteiben kell a minta értéktartományát módosítani.
3. A sokaság és a minta bemenő adatai
   Itt kell megadni a számítások elvégzéséhez szükséges adatokat, ahogyan azt az előző cikkben már tárgyaltam. A sokaság adatait be kell gépelni, a minta adatait pedig – ahogyan azt már korábban említettem – be lehet vinni egyenként, vagy felül lehet írni a minta átlagának és a minta elemszámának számítási képletét. A minta tulajdonságait az ÁTLAG() és a SZÓRÁS() függvények segítségével számoltam ki.
4. A teszt eredményei
   Itt először kiszámítom Z értékét az előző cikkben megismert módon, tehát kiszámítom, hogy a minta átlaga „hány szórásnyira” van a sokaság átlagától. Azért másoltam ide a cellák sor és oszlop azonosítóit is, hogy ha valaki követni akarja a képlet felépítését, azt meg tudja tenni.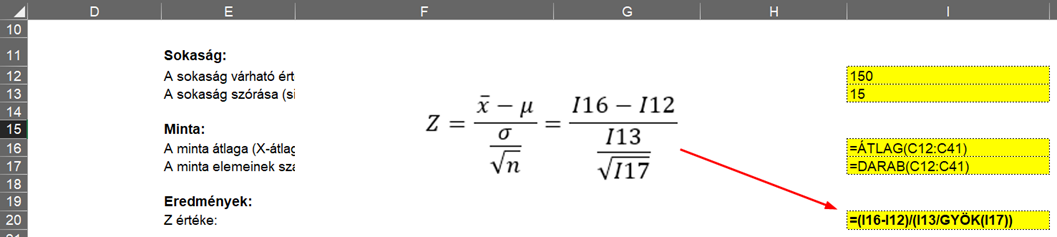
   
   A Z-érték alatt lévő táblázat tartalmazza az alsó és a felső határértékeket (’Z-limit-’ és ’Z-limit+’), ezek alapján tudjuk eldönteni, hogy elfogadjuk vagy elutasítjuk a nullhipotézist. Mivel korábban már tisztáztuk, hogy standard normál eloszlás csak egy van (Első az egyenlők között – a standard normál eloszlás), ezért itt nem kell szórakoznunk azzal, hogy egyenként kiszámítjuk a határértékeket minden egyes teszt esetre, mivel ezt mások már megtették helyettünk. A ’Döntés’ oszlopban már csak egy HA() függvénnyel el kell döntenünk, hogy elfogadjuk vagy elutasítjuk a nullhipotézist. Itt csak arra kellett ügyelni, hogy Z értékét mindig a megfelelő határértékkel hasonlítsam össze. A jobb láthatóság kedvéért a szorgalmas olvasók feltételes formázással hozzáadhatnak az eredménytől függő színt (zöld, ha elfogadjuk, piros, ha elutasítjuk a nullhipotézist). Végül kiszámítottam megbízhatósági intervallumokat a különféle teszt esetekre. Ezek megmutatják, hogy a sokaság várható értékének (átlagának) milyen tartományban kell lennie ahhoz, hogy a nullhipotézist elfogadjuk. Az ehhez alkalmazott képletet szintén ismertettem az előző bejegyzésben.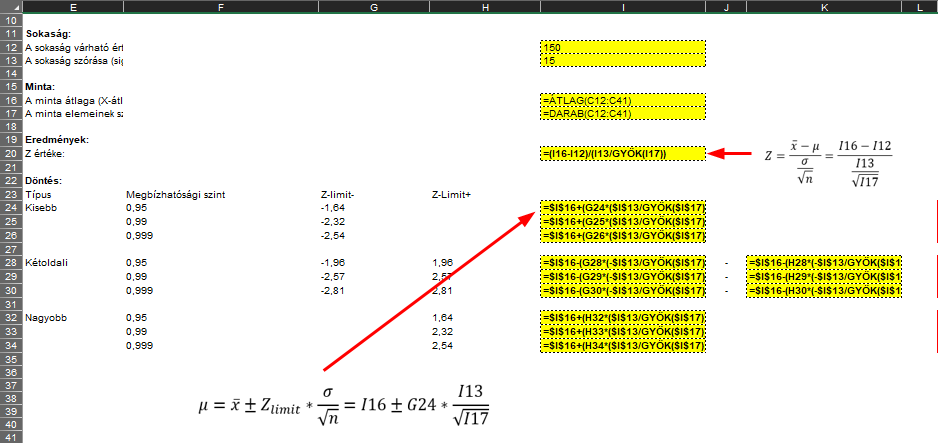
   
   
   

5. A teszt végeredménye
   Véleményem szerint mindig fontos, hogy szöveggel is megfogalmazzuk a teszt eredményei alapján leszűrt következtetéseinket. A teszt szöveges összefoglalása megteremti a kapcsolatot az adatok feldolgozása és a valóság között. Egy kicsit olyan ez, mint egy szöveges feladat megoldása: nem a képlet a fontos, hanem az, hogy megoldjunk egy problémát. Sajnos ez sokszor elmarad, pedig ez nemcsak a laikusoknak fontos, de nekünk is, amikor az ötszázadik teszt után is szeretnénk visszaemlékezni arra, hogy mit is állapítottunk meg a teszt alapján.
   

6. A lap utolsó része igazából csak egy magyarázó ábra, amely bemutatja az egyoldali és a kétoldali hipotézis vizsgálatok jelentését. Ugyanez az ábra megtalálható hipotézisvizsgálatokról szóló bejegyzésben (Igaz vagy hamis – a hipotézis vizsgálatokról…).

Végül a táblázatkezelőben készített riport így néz ki:

Összehasonlításképpen bemutatom, hogy a Minitab – egy professzionális statisztikai szoftver – milyen eredményt ad ugyanerre a problémára. Az egymintás Z-próba a ’Stat’ menüben, a ’Basic Statistics’ almenüben található.

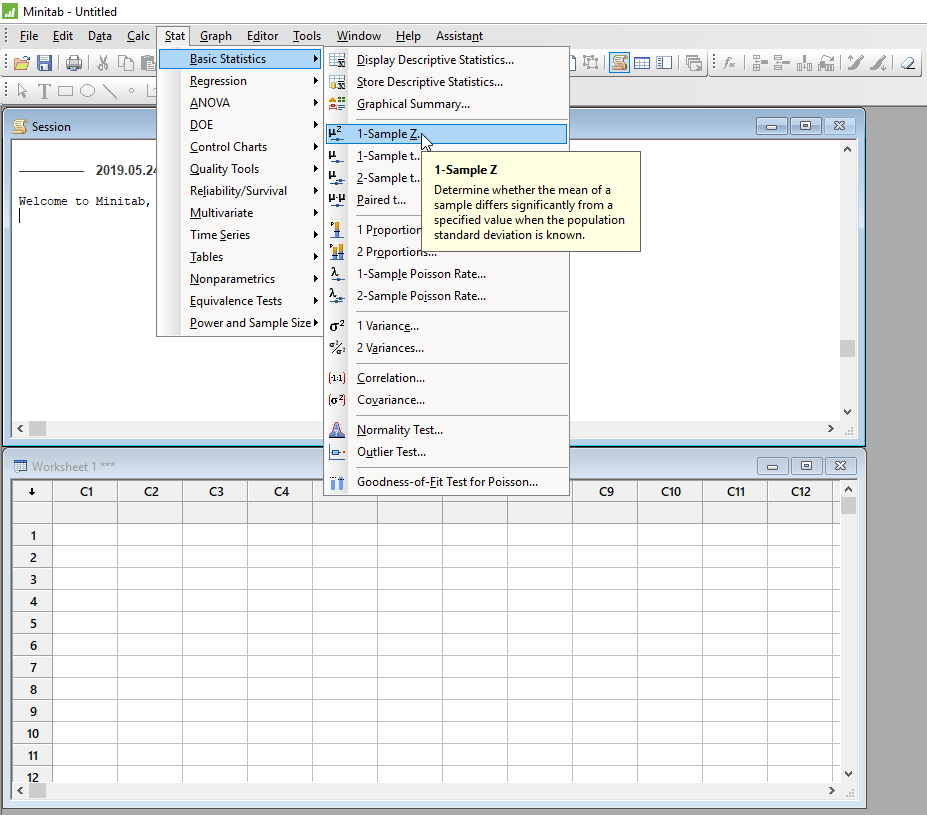
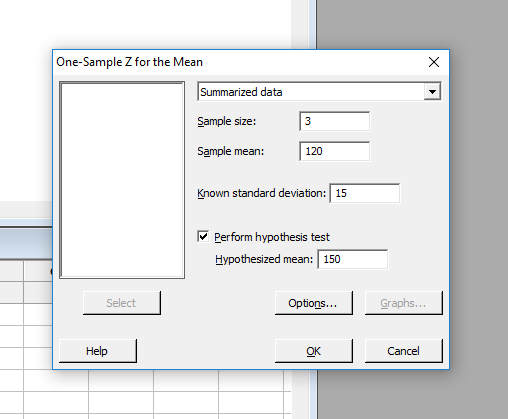
A menüparancs meghívásakor megjelenő adatbeviteli ablakban először kijelöltem, hogy összegzett adatokból dolgozzon, azaz kiválasztottam jobboldalt fent a ’Summarized data’ pontot a legördülő mezőben, majd sorban beírtam a megfelelő adatokat az ablak megfelelő mezőibe.

• Értelemszerűen a ’Sample size’ jelenti a minta elemeinek számát, amely ez esetben 3.
• A ’Sample mean’ jelenti a minta átlagát, amely ez esetben 120.
• A ’Known standard deviation’ a sokaság szórása, amelyről tudjuk, hogy 15.
• Ezután bejelöljük a ’Perform hypothesis test’ mezőt és beírjuk a sokaság átlagát (150) a ’Hypothesized mean’, azaz elméleti átlag mezőbe.

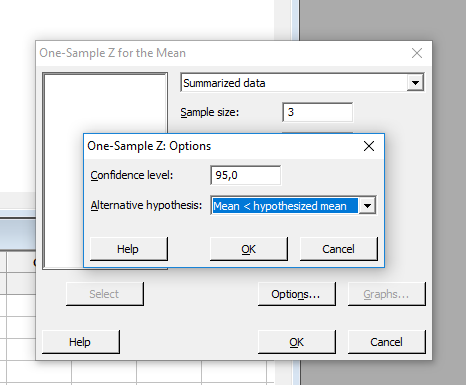
Végül az ’Options’ gombra kattintva megjelenik egy újabb ablak, amelyben beállíthatjuk a hipotézis vizsgálat típusát, valamint a megbízhatósági szintet. Ez esetben a ’Mean < hipothesized mean’ opciót választottam, mert a minta átlaga kisebb, mint a sokaság átlaga, illetve a ’Confidence level’ mezőt változatlanul hagytam 95%-on, mert ezt szeretném megbízhatósági szintnek.

Miután az ’OK’ gombbal bezárjuk mindkét ablakot, a Minitab a következő összefoglaló riportot nyomtatja ki:

A ’One-Sample Z’ jelenti a teszt típusát, tehát azt, hogy egymintás Z-próbát készített a szoftver. A következő sorban adja meg a nullhipotézist és az ellenhipotézist rövidített formában, majd megadja, hogy a sokaság feltételezett szórása (The assumed standard deviation) 15. Ezután részletezi a minta jellemzőit, úgymint, hogy a minta elemeinek száma (N) 3, a minta átlaga (Mean) 120, az átlag standard hibája (SE Mean) 8,66 illetve, hogy a 95%-os megbízhatósági intervallum felső határa (95% Upper Bound) 134,24. Ezután szerepel Z értéke, amely -3,46, illetve egy titokzatos ’P’ betű, amely alatt 0,000 szerepel. Ez a P-érték a későbbiekben fontos lesz nekünk, de erről majd egy következő bejegyzésben szeretnék írni, mert ez egy kicsit hosszabb lélegzetű téma.

Tehát tisztáztuk, hogy mi mit jelent, de akkor most mi az eredménye a tesztünknek? Milyen következtetést tudunk leszűrni Samu kijelentéseivel kapcsolatban. A riport így tisztán statisztikai nyelven íródott, tehát le kell fordítanunk azt a saját nyelvünkre. A következtetéseket így nem könnyű leszűrni, hiszen a riport nem tartalmazza a standard normál eloszláshoz tartozó határértéket, amelyet alkalmazott. Így csak két dologra hagyatkozhatunk:

Az egyik a fent említett titokzatos P-érték, amelynek 0,05-nél nagyobbnak kell lennie ahhoz, hogy a nullhipotézist elfogadjuk.

A másik, hogy a 95%-os megbízhatósági intervallum felső határa (95% Upper Bound) 134,24 pont, azaz jelentősen kisebb, mint a nullhipotézisben megadott 150 pont, így a nullhipotézist elutasítjuk.

Tanulságok:

Sajnos a kétféle riport összehasonlításából jól látható, hogy a professzionális statisztikai szoftverek úgy vannak megírva, hogy egy laikus tudjon döntéseket hozni az alkalmazásukkal, de lehetőleg minél kevesebbet értsen meg ezek hátteréről, illetve a szoftver döntési mechanizmusairól, vagyis a felhasználó használja a szoftvert, de ne értse, egyébként nem lesz hajlandó fizetni érte. Az viszont igaz, hogy a profik meg úgyis értik a riportot, nincs szükségük további magyarázatra.

A táblázatkezelőben elkészített jelentést persze rugalmasabban tudjuk az igényeinkhez igazítani, viszont nagyon vigyáznunk kell a számítások helyességére és a képlethibák elkerülésére, amelyeket nekem is sikerült többször elkövetnem jelentés elkészítése során. Nagyon fontos a kész jegyzőkönyv ellenőrzése teszt adatokkal és utána a képleteket tartalmazó cellák lezárása az utólagos módosítások elkerülése érdekében.