Amint azt már megszokhattad, ismét bemutatom, hogy az előző cikkben (Legyőzik a majmok a brókereket? – Egymintás Z-próba az előfordulás gyakoriságának vizsgálatára (Test for 1-Proportion)) ismertetett teszt végrehajtását táblázatkezelőben és a Minitab statisztikai programmal.

Ez most egy kicsit izgalmasabb volt, mint szokott, mert a táblázatkezelős és a Minitab verzió készítése közben jöttem rá, hogy elszámoltam az egészet, szóval írhattam a fél cikket újra (mármint az előzőt). Istenem, jobb családban is előfordul az ilyesmi. A lényeg, hogy most már minden passzol, csak a pontosság kedvéért hat tizedesjegyig kellett alkalmazni az értékeket, illetve a táblázatkezelőben érdemes volt a 61% helyett képletként bevinni az adatokat, például =90/147 vagy =80/147. De ezek az apróságok nem vesznek sokat a történet élvezeti értékéből. Hát akkor lássunk neki…

A táblázatkezelőben az egymintás Z-próba lapját másoltam le és alakítottam át a 1-proportion teszt elkészítéséhez. Ebből kifolyólag a tábla szerkezete nem változott lényegesen, csak az egyedi adatok bevitelére szolgáló mezőket tüntettem el lustaságból, mert úgy döntöttem, hogy ez esetben csak szimplán veszem a gyakoriságokat, és azzal fogok számolni. A táblázatom fejléce így néz ki:

Eddig minden ugyanaz, a teszt típusának természetesen a jobboldali megbízhatósági modellt választottam, hiszen a 61% nagyobb, mint a célként kiválasztott 50%.

A sokaság adatainál megadtam a várható értéket, ami eléggé egyértelmű, a szórás esetében viszont képlettel számíttattam ki a cella értékét a táblázatkezelővel. Az I12 cellában természetesen a sokaság várható értéke, azaz 0,5 szerepel.

A minta átlagát nem számmal, hanem képlettel adtam meg, mert a táblázatkezelő így pontosabban számol.

Z értékének kiszámítása az előző bejegyzésben leírtak szerint történt meg, semmi különleges nem történt. Az I16 cellában van a minta átlaga (p), az I12 cellában a sokaság átlaga (p0). Az I13 cellában a sokaság szórása szerepel (Sigma = GYÖK(p * (1 - p))), az I17 cellában pedig a minta elemeinek száma (n).

A riport eddig így néz ki, Z értékére szépen ki is jött az előző bejegyzésben kapott 2,72.

Ami még hátravan, az a Z-határértékek kiszámítása a különféle teszt típusokra és megbízhatósági szintekre. Az átláthatóság kedvéért újra elmagyarázom, hogy a megbízhatósági intervallumokat a használt minta értékei alapján számítom ki, azt becsülöm velük, hogy a minta átlaga és szórása alapján mekkora lehet a sokaság átlaga. Z értékének kiszámításakor a sokaság szórását használtam, a megbízhatósági intervallumok határértékeinek kiszámításához viszont a minta szórását fogom használni. Ezt nem számoltam ki előre egy külön cellában, hanem beleírtam a képletbe.

Az érthetőség kedvéért idemásolom a megbízhatóság intervallum kiszámításának képletét, ennek ismeretében a cellában található képlet könnyen értelmezhető. Az I16 mező tartalmazza a minta p értékét, a H32 cella pedig a standard normál eloszlás 95%-os megbízhatósági szintjéhez tartozó jobboldali határértékét.

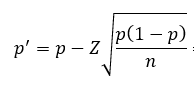
Ne tévesszen meg, hogy a jobb oldalon a döntés mezőben van olyan sor, ahol az van odaírva, hogy a „Nullhipotézis elfogadva”. Mivel a teszt elején eldöntöttem, hogy jobboldali tesztet fogok készíteni, ezért csak a jobboldali teszt eredményét fogom figyelembe venni, ez pedig el van utasítva. A teszt végeredménye végül is így néz ki:

Akkor most hasonlítsuk össze az eredményt a Minitab által generált eredményekkel. A Minitab-ban az előzőekhez hasonlóan indítottam el a tesztet:

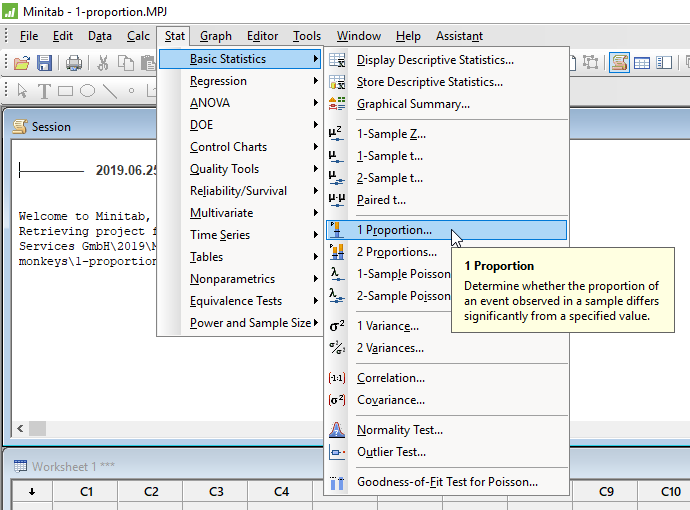
A megjelenő adatbeviteli ablakban először kiválasztottam az ablak jobb felső legördülő párbeszéd mezőjében a ’Summarized data’ opciót, mert csak az összegzett adatokat akarom megadni. Ha a nyers adatokat hoztam volna át, azokat a ’One or more samples, each in a column’ potot választottam volna.

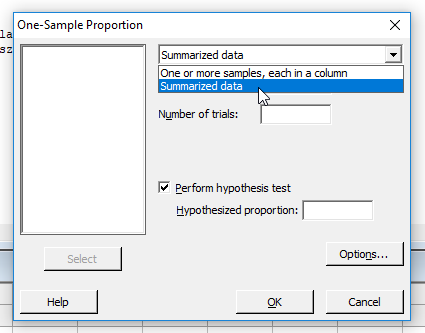
Ezután megadtam a teszt kiinduló adatait. A ’Number of events’ mezőben kell megadni azt, hogy hány eseményt észleltünk, jelen esetben azt, hogy hányszor nyertek a szakértők a darts nyilak ellen. A ’Number of trials’ jelenti azt, hogy hány forduló volt összesen, itt 147 hónap adatait összegeztem. Ha kipipálom, akkor hajtja végre a program a hipotézis vizsgálatot. A ’Hypothesized proportion’ mezőbe kell beírni a sokaság átlagát, jelen esetben 0,5-öt.

Az ’Options…’ gomb megnyomásával megjelenik egy újabb ablak.

A ’Confidence level’ jelenti a kívánt megbízhatósági szintet, ez esetben is a jól bevált 95%-ot választom (0,95). Az ’Alternative hypothesis’ esetében azt választottam ki, hogy a minta gyakorisága nagyobb, mint a sokaság gyakorisága, azaz ’Proportion > hypothesized proportion’. Ez tulajdonképpen a teszt típusa, azaz ez egy egyoldali, jobboldali teszt.

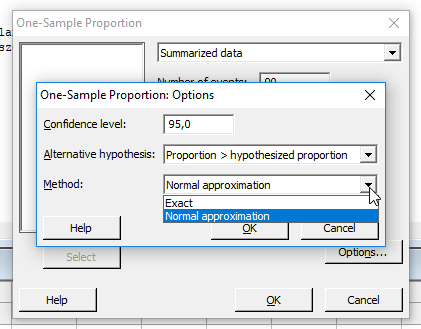
A ’Method’ mezőben a ’Normal approximation’ pontot kell kiválasztanom, az ’Exact’ teszt teljesen más képletekkel számol. A fenti beállításokkal a következő eredményt kapjuk:

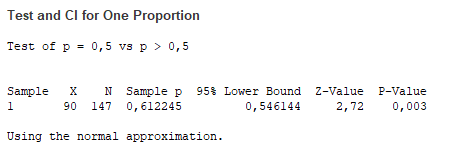
A test szokásosan a nullhipotézis és az ellenhipotézis megadásával kezdődik, majd jön maga a konkrét hipotézis vizsgálat. ’X’ és ’N’ értéke egyértelmű a példa alapján. A ’Sample p’ tartalmazza a ’p’ értékét, amely a „p = X / N” képlettel számítható. A ’Z-value’ ugyanaz a 2,72, amelyet már kétszer kiszámoltunk más módszerekkel, a ’95% Lower Bound’ a konfidencia intervallum alsó vége, tehát az a legkisebb érték, amelyet a sokaság átlaga a minta alapján még felvehet. Itt az első döntési kritérium, mivel a nullhipotézisben megadott 0,5 nem lehet nagyobb, mint 0,546144, ezért a nullhipotézist elvetem és az alternatív hipotézist fogadom el. A ’P-Value’ pedig a titokzatos ’P’, akit még mindig nem mutattam be. Lassan olyan lesz, mint Columbo felesége… Ettől függetlenül a P-értékről annyit tudunk, hogy a 0,003 kisebb, mint 0,05, ezért a nullhipotézist elutasítjuk.

Ha a szakértők teljesítményét a Dow Jones Industrial Average teljesítményével is össze akarom hasonlítani, akkor újra elő tudom hívni ugyanazt az ablakot ugyanazokkal az értékekkel a lent látható gomb megnyomásával.

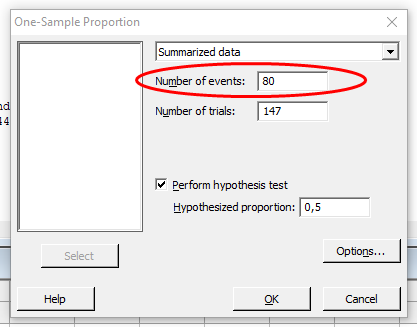
A megjelenő ablakban elég a ’Number of events’ mezőben a 90-et átírom 80-ra, és kész is vagyok.

Az eredmény ez esetben is megegyezik a korábbi – más eszközökkel elvégzett – számításokkal.

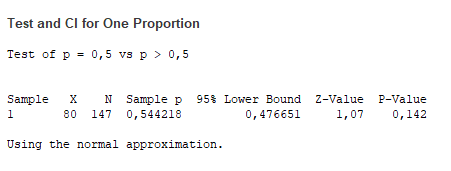
Nyilván ’Sample p’ értéke 61%-ról 54%-ra változott, ezzel párhuzamosan A ’95% Lower Bound’ kisebb lett, mint 0,5 és a Z-érték is kisebb lett, mint a korábban használt 1,64 határérték. A ’P-Value’ értéke jelen esetben 0,142, ami jelentősen nagyobb, mint 0,05, ezért a nullhipotézist ez esetben elfogadom.