
A címben szereplő Poisson-eloszlás egy kicsit különleges a korábban bemutatott eloszlásokhoz képest. Az eddig ismertetett eloszlások esetében azt vizsgáltuk, hogy ha van n darab esetünk, akkor abból mekkora valószínűséggel fognak esetek megfelelni egy adott feltételnek, például nagyszámú érmefeldobás esetében mekkora a valószínűsége annak, hogy fej vagy írás lesz az eredmény (A Bernoulli-eloszlás - a világ "legegyszerűbb valószínűségszámítási kísérlete") vagy hogy mekkora a valószínűsége annak, hogy nagyszámú dobókocka dobás esetén mekkora a valószínűsége annak, hogy hatost dobunk, vagy hogy vagy 10 dobás eredményének átlaga 4-nél nagyobb lesz (A nagy dobókocka kísérlet).
A Poisson eloszlás esetében egy kicsit más a helyzet, mert itt olyan helyzeteket vizsgálunk, amikor azt meg tudjuk számolni, hogy egy adott feltételnek megfelelő eset hányszor fordul elő, azt viszont NEM tudjuk megszámolni, hogy hány olyan eset van, amikor az eset NEM FELEL MEG a megadott feltételnek!
Ez most mit is jelent? Nézzünk egy pár példát:
- Közlekedési balesetek esetén meg tudjuk számolni, hogy egy év alatt vagy egy adott útszakaszon hányszor történt baleset, de azt nem tudjuk, hogy hányszor NEM TÖRTÉNT BALESET.
- Egy ritka betegség előfordulása esetében meg tudjuk számolni, hogy egy év alatt hányan betegedtek meg ebben a betegségben, de azt nem tudjuk, hogy hányan NEM BETEGEDTEK MEG.
- Azt meg tudjuk mondani, hogy egy tekercs szövetben hány szövési hiba van, de azt nem tudjuk, hogy hány szövési hiba NINCS A SZÖVET TEKERCSEN.
- Azt tudjuk, hogy hányan vettek fel pénzt egy óra alatt egy ATM-ből, de azt nem tudjuk, hogy hányan NEM VETTEK FEL PÉNZT az ATM-ből egy óra alatt.
- Azt tudjuk, hogy hány gyermek születik egy évben Magyarországon, de azt nem tudjuk, hogy hány gyermek NEM SZÜLETETT MEG.
- Azt tudjuk, hogy hány hullócsillagot látunk egy óra alatt az égen, de azt nem tudjuk, hogy hány hullócsillagot NEM LÁTUNK.
Ezekben az esetekben – a teljes sokaság ismerete híján – nem tudjuk a korábban már megismert eloszlásokat alkalmazni az események előfordulási valószínűségének becslésére, hiszen nem ismerjük a teljes sokaságot. Egy valamit azért mégiscsak tudunk, ami összeköti a fent felsorolt eseteket, mégpedig az, hogy azt viszont vizsgálni tudjuk, hogy az adott feltételnek megfelelő esetek hányszor fordulnak elő egy adott fizikai mennyiség egységnyi mennyiségében! Ez a bizonyos fizikai mennyiség legtöbbször időegységet jelent, de nem feltétlenül. A szöveten lévő szövési hibák esetében ez a fizikai mennyiség a szövet területe, illetve a szövettekercsek száma, de ezzel az erővel azt is el tudnám képzelni, hogy a fizikai mennyiség mondjuk a térfogat, ha mondjuk azt akarjuk megbecsülni, hogy hány ózon molekula van 1 köbméternyi levegőben.
A Poisson-eloszlás alkalmazásához egyetlen információ ismerete szükséges, mégpedig az, hogy korábban a vizsgált fizikai mennyiség (idő, távolság, tömeg, térfogat) egységnyi mennyiségében átlagosan hányszor fordult elő az adott feltételnek megfelelő esemény.
A Poisson-eloszlást először Simeon-Denis Poisson, egy híres francia matematikus – kora francia tudományos életének ismert alakja - tárgyalta egy kevésbe tudományosnak ható címmel 1837-ben megjelent könyvében (Research on the Probability of Criminal and Civil Verdicts – A büntető és a polgári ítéletek valószínűségeinek tudományos vizsgálata). A könyv maga csak három évvel Poisson halála előtt jelent meg, így az ebben foglaltaknak nem volt igazán átütő tudományos hatása. A Poisson-ról elnevezett eloszlás végül Ladislaus Josephovich Bortkiewicz lengyel matematikusnak köszönhetően került be a köztudatba, aki 1898-ban publikált egy könyvet Das Gesetz der kleinen Zahlen – A kis számok törvénye címmel, amelyben olyan példákon keresztül mutatta be a Poisson-eloszlás működését, mint a 20 év alatt a Porosz hadsereg lovassági egységeiben „baráti” lórúgások miatti halálozások száma, vagy azon gyerekek száma, akik öngyilkosok lettek Poroszországban.
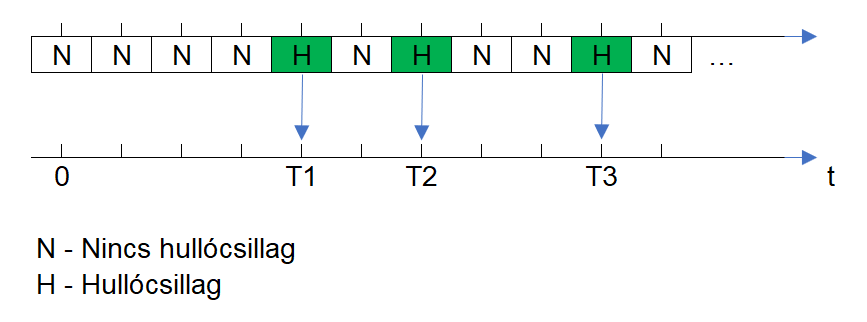
A Poisson eloszlás alapötlete tulajdonképpen annyi, hogy a problémát egy egyszerű trükkel visszavezeti a Bernoulli-eloszlásra. Vegyük például az egy óra alatt látható hullócsillagok számát. Egy kellemes felhőtlen éjszakán szerencsés esetben akár 5-6 hullócsillagot is láthatunk egy órán belül. Ha ezt az egy órát felosztjuk nagyon sok nagyon rövid időperiódusra, akkor azt fogjuk kapni, hogy lesznek olyan időpillanatok, amikor látunk hullócsillagot és lesznek olyanok, amikor nem. Ez majdnem olyan, mintha minden egyes pici időpillanatban feldobnánk egy érmét, és ha fej az eredmény, az azt jelenti, hogy láttunk hullócsillagot, az írás pedig azt, hogy nem. Mivel a hullócsillagok megjelenése nem függ egymástól ugyanúgy, ahogy az egyes érmefeldobások is egymástól függetlenek.
Tegyük fel, hogy már sokszor feküdtünk kinn a szabad ég alatt a hullócsillagokat számolva és ismerjük, hogy átlagosan hány hullócsillagot szoktunk látni egy óra alatt. Ezt a számot nevezzük el λ-nak (azaz lambdának). Az időegységek számát, amelyekre az egy órát felosztottuk nevezzük el n-nel, az időegységek hosszát pedig nevezzük el δ-val (azaz deltával). Így kaptunk n darab δ hosszúságú idődarabkát, amelyeknek a teljes hossza 1 óra.
De ennek az 1 órának mekkora része, azaz hány perc lesz az, amikor látunk hullócsillagot? Ha ezt meg tudjuk adni, akkor „közös alapra” hoztuk a „hullócsillagos” és a „nem hullócsillagos” időtartamokat, így egy egyszerű osztással meg is lesz a keresett valószínűség.
A Poisson-eloszlás képletének levezetése innentől egy kissé elbonyolódik, de ha érdekel, akkor a következő linken találsz egy relatíve érthető levezetést:
A lényeg, hogy annak a valószínűsége, hogy adott időegység alatt k (k = 1, 2, 3, …) darab esemény bekövetkezik, a következő képlettel számolható ki:
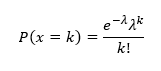
ahol
- e – az Euler-féle szám
- λ – Az esemény átlagos várható mennyisége időegységenként (korábbi tapasztalatok alapján)
- k – Az esemény keresett átlagos előfordulásainak száma
- k! – k-faktoriális, azaz 1*2*3…*k
Ez azt jelenti, hogy egy adott esemény időegységenkénti előfordulásainak a száma igazából nem függ mástól, csak a korábbi tapasztalatoktól. Nézzük meg, hogyan működik a Poisson-eloszlás egy példán keresztül, legyen ez mondjuk a hullócsillagos példa. Ha feltételezzük, hogy korábban azt tapasztaltuk, hogy átlagosan 2 hullócsillagot láttunk óránként (ez lesz a λ), és arra vagyunk kíváncsiak, hogy mekkora a valószínűsége annak, hogy most k = 3 hullócsillagot fogunk látni, akkor λ és k értékét behelyettesítve a fenti képletbe, megkapjuk, hogy
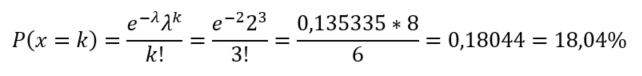
a valószínűsége annak, hogy 3 hullócsillagot fogunk látni egy óra alatt. És hogyan viselkedik ez a függvény különböző λ várható értékek és k előfordulások esetében?
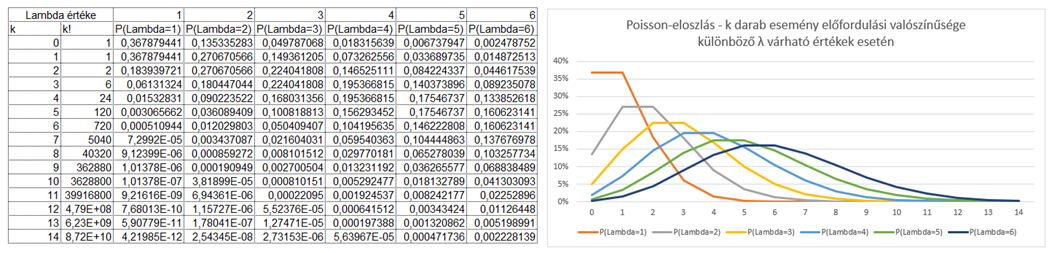
Minél nagyobb λ értéke, annál inkább ellaposodik a függvénygörbe, tehát egy-egy k-érték előfordulási valószínűsége annál kisebb lesz. Ezzel párhuzamosan jól látható, hogy a görbék legmagasabb pontja mindig az éppen aktuális lambda érték körül lesz, azaz a Poisson-eloszlás átlaga vagy várható értéke pontosan λ lesz! Ez szerintem logikus, hiszen, ha eddig azt tapasztaltam hosszú idő alatt, hogy mindig 2 hullócsillagot látok óránként, akkor miért várnék ez esetben mást? A történet annyiban bonyolódik, hogy amennyiben nem arra vagyunk kíváncsiak, hogy 1 óra alatt mennyi hullócsillag várható, hanem mondjuk 6 perc alatt hány hullócsillag várható, akkor természetesen λ értékét meg kell szorozni 0,1-gyel, hiszen 6 perc az 0,1 óra. Ezek alapján az eloszlás várható értéke
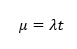 A Poisson eloszlás abból a szempontból érdekes, hogy a varianciája ugyanannyi, mint az átlaga, azaz λ*t.
A Poisson eloszlás abból a szempontból érdekes, hogy a varianciája ugyanannyi, mint az átlaga, azaz λ*t.

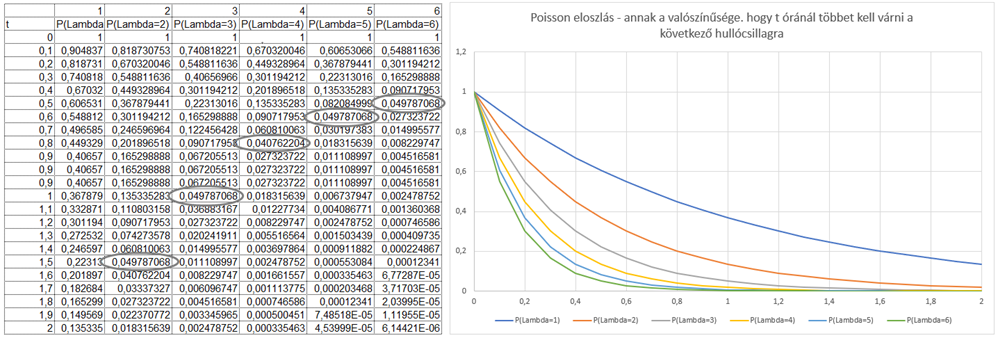
A következő érdekes kérdés az lehet, hogy mennyi az a várható időtartam, ameddig várnunk kell a következő hullócsillagra. A fenti esetben például feltehetjük a kérdést, hogy mekkora a valószínűsége annak, hogy a következő t = 6 percen belül látunk majd egy újabb hullócsillagot. Ezt a valószínűséget a következő módon számíthatjuk ki:
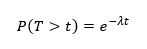
Ha a hullócsillagok száma a hosszútávú tapasztalataink alapján 2 darab óránként, akkor annak az esélye, hogy a következő 6 percben látunk majd egy újabb hullócsillagot
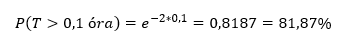
Ez azt jelenti, hogy több, mint 80% a valószínűsége annak, hogy 6 percnél – azaz 0,1 óránál – többet kell várnunk a következő hullócsillagra. Készítettem egy hasonló táblázatot és grafikont erre a problémára is. Ez alapján azt állapítottam meg, hogy ha óránként 2 darab hullócsillagra számítunk, akkor 95%-os valószínűséggel legalább másfél órát kell várnunk a következő hullócsillagra. Nyilván minél nagyobb az óránként látható hullócsillagok aránya, annál rövidebb ideig kell várnunk a következő hullócsillag észlelésére, így, ha átlagosan 6 hullócsillagra számítunk, akkor már csak fél órát kell várnunk.
Amint azt a cikk elején is olvashattad, a Poisson-eloszlás az élet legkülönfélébb területein kerülhet elő és időnként nem könnyű felismerni, hogy egy adott probléma esetén ezt az eloszlást kell alkalmazni. A cikk elején leírt példák segíthetnek a felismerésben, de az eloszlás alkalmazása igényelhet némi gyakorlatot és tapasztalatot annak ellenére, hogy a számítások relatíve egyszerűek.





