
A legendás Sidney - Hobart yachtverseny a világ egyik legnehezebb hajóversenye, a yacht versenyek Everest-jeként is emlegetik. A verseny során az ausztráliai Sidney-ből kell eljutni a Bass szorost keresztezve Tasmánia fővárosába, Hobart-ba. A verseny minden évben nagy esemény, amelyet Karácsony másnapján indul el, hogy azután az indulók 2-6 nap alatt eljussanak a 630 tengeri mérföldre lévő célig.

A Bass-szoros Ausztrália és Tasmánia között található körülbelül 300 kilométer hosszú tengerszoros, amely a Tasmán-tengert köti össze az Indiai-óceánnal. Ez a terület híres az erős szelekről és a szeszélyes hullámzásról. A verseny nagy része a Tasmán-tengeren zajlik, a verseny útvonalának közelében lévő sekély tengerszorosnak erős hatása van a verseny körülményeire. Noha a versenyt az Ausztrál nyárban rendezik, az erre a területre jellemző gyakran váltakozó viharos szelek miatt a verseny gyakran van hideg, a magas hullámok miatt az út egyenetlen és ezért nagy kihívást jelent a versenyzők számára. A bal oldali ábra mutatja meg a viharos időjárás kialakulásának fő okát, a jobb oldali pedig a hullámok magasságát, illetve a szél sebességét adja meg az 1998-as verseny során. A hullámok átlagosan 3-5 méter körüli, de voltak olyan hullámok is, amelyek elérték a 10-12 méteres magasságot is. A szél sebessége elérte a 64 csomós (~120 km/órás) sebességet is!
Az esemény eredetileg nem versenynek indult, Peter Luke és barátai egyszerű átkelést terveztek, de John Illingworth kapitány, a Királyi Haditengerészet tisztje azt javasolta, legyen inkább verseny. A legelső versenyen végül 9 hajó indult el és végül a kihívó, John Illingworth nyerte meg a versenyt ’Rani’ nevű hajójával. Azóta minden évben megrendezik az eseményt, amely egyfajta megmérettetést jelent a tengeri vitorlázók számára.
Ami a számomra is érdekessé tette ezt a versenyt az az, hogy a verseny Wikipédia oldalán közzétették az eddigi összes verseny győzteseit és azok időeredményeit. Természetesen ez egy remek alkalom arra, hogy elemezük egy kicsit ezt az adatsort. Már az első pillanatban szembetűnik, hogy mennyit javultak az időeredmények a verseny története során. Az első versenyzőknek még több, mint 6 napra volt szükségük az út megtételéhez, míg a legutóbbi versenyeken már alig több, mint egy nap is elég volt az átkeléshez.
Nézzük meg, hogyan néznek ki az adatok az idő függvényében:

Jaj de szép! Igazán szépen látszik, hogy az eltelt évtizedek során hogyan javultak az időeredmények. Természetesen az egyedi értékeknek van valamekkora szórása, de a trend ragyogóan látszik. Csak a kíváncsiság kedvéért kiszámoltam az évek és a győztes időeredmények közötti korreláció mértékét (Valaki átírta a korrelációs együttható képletét, hogy ne lehessen érteni? Ez most komoly…?).

Amint az látható, a korrelációs együttható értéke kb. -90% lett, ami ugye egy erős negatív korrelációt jelent. Noha erre semmilyen tudományos érv nem létezik, én a magam részéről neki sem kezdek a regresszió elemzésnek, ha a korrelációs együttható nincs 0,9 vagy -0,9 közelében. Ez nem általános szabály, ez csak az én saját külön bejáratú szabályom, vitatkozni lehet vele. Persze előfordul, hogy vannak kieső értékek, vagy olyan magyarázható mintázatok, amelyeket adott feltételek mellett ki lehet zárni. Végül is azért akarjuk meghatározni a regressziós egyenes egyenletét, mert jelen esetben szeretnénk megjósolni, hogy vajon körülbelül mennyi lesz a győztes időeredmény mondjuk 2030-ban, ez viszont nem ad megbízható eredményeket, ha a két változó korrelációja eleve nem elég erős.
A korábban megjelent bejegyzéseimben már összefoglaltam a regresszió elemzés elméleti hátterét:
- A Miért kevés közöttünk az óriás és a törpe? című írásban összefoglaltam a regresszió elemzés kialakulásának történetét,
- A Legyenek a négyzetek minél kisebbek…! – útban a lineáris regresszió elemzés felé című cikkben bemutattam a legkisebb négyzetek módszerét, amely tulajdonképpen a regresszió elemzés elméleti alapja,
- A Tudom, hogy gőzgép, de mi hajtja? – Egyváltozós lineáris regresszió – a regressziós egyenes meghatározása című bejegyzésben pedig ismertettem a regressziós egyenes meghatározásának elméleti hátterét.
Most pedig rakjuk össze mindezeket az ismereteket, és alkalmazzuk az eddig megtanultakat egy gyakorlati példán!
A teljes táblázat a következőképpen néz ki:

A bal felső sarokban lévő diagramot már bemutattam, most részletesen ismertetem majd a számítás menetét. Amint azt már korábban megtudtuk, egy egyenes egyenletét keressük, amelynek a formája y = ax + b. A feladat a és b értékének meghatározása.
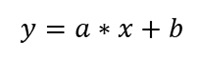
Az ’a’ változó értékének meghatározásához a következő képletet alkalmazzuk:
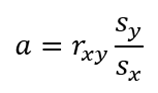
Ehhez viszont ki kell számolnunk Sy, Sx és rxy értékeit. Mindhárom képlet jelentését részletesen ismertettem a fentebb említett bejegyzésekben, érdemes ezeket is átolvasni a jobb megértés kedvéért. Az évek és a győztes időeredmények szórása a következőképpen néz ki:
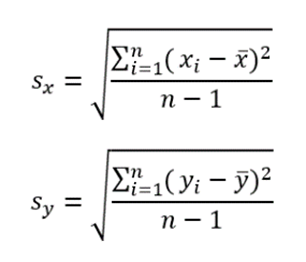
Ahogyan azt már fentebb láttuk, a korrelációs együttható pedig a következő képlettel számítható ki:
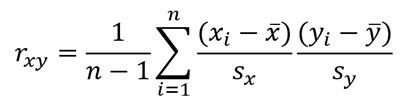
A szórások kiszámításához először is kiszámítottam az évekre és a győztes időeredményre vonatkozó adatsorok átlagát, …
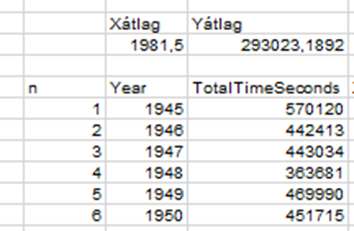
… majd az adatsorok összes elemére kiszámítottam az Xi - X̅, valamint az Yi - Y̅ különbségeket, majd ezek négyzetét is. Természetesen ide csak a táblázat első elemeit másoltam be, de természetesen az adatsor mind a 74 elemét tartalmazza a táblázat. A jobb felső sarokban kiszámítottam az Sy és az Sx szórások képletében a számlálók értékeit.

Ezután már csak az a feladat maradt, hogy a fent kiszámított számlálók értékeit el kellett osztani n-1-gyel, azaz 73-al, majd e hányadosokból gyököt kellett vonni.

A korrelációs együttható kiszámítása hasonló módon történik, az 'rxySum' mező a fentebb bemutatott képletben a szumma jel utáni képlet eredménye:

Ezután ezt az összeget is csak el kellett osztani n-1-gyel és meg is kapjuk rxy értékét.

Innen 'a' értékének kiszámítása már gyerekjáték, hiszen csak be kell helyettesíteni a fent kiszámított értékeket a egyenletébe.
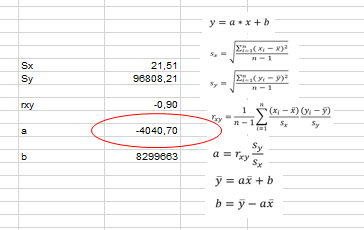
'b' értékét úgy kapjuk meg, hogy a regressziós egyenes képletébe beírjuk a, x̅ és y̅ értékeit, és kifejezzük az egyenletből 'b'-t.
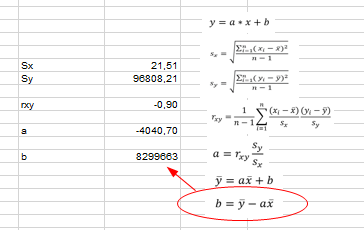
Hurrá! Megkaptuk a keresett egyenes mindkét tényezőjének értékét, így nincs más dolgunk, minthogy rárajzoljuk az egyenest a korábban bemutatott scatter-diagramra. Ehhez készíthetünk egy külön táblázatot, ahol minden egyes évhez kiszámoljuk, hogy az adott évben mennyi a kapott regressziós egyenlet alapján kapott érték:
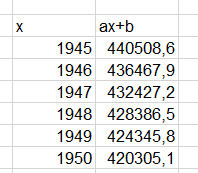
Ezt az adatsort hozzáadva a korábban bemutatott diagramhoz jól láthatjuk, hogy az egyenesre szépen illeszkednek az adatpontok, vagyis valószínűleg nem végeztünk rossz munkát.
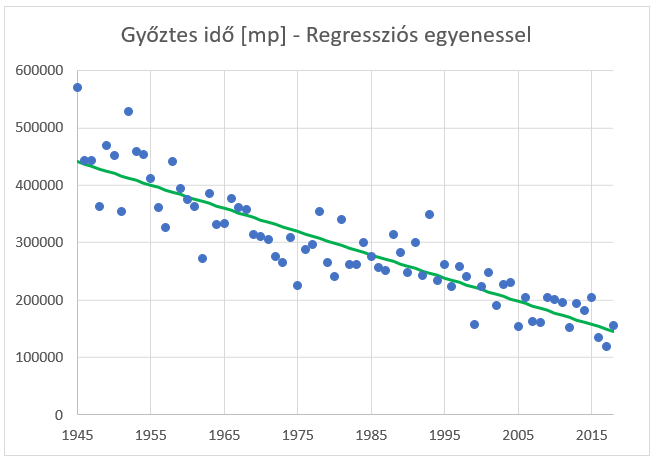
A regressziós egyenes egyenlete tehát a következő:

Utolsóként annyi feldatunk maradt, hogy kiszámítsuk, mennyi lenne a győztes idő 2030-ban
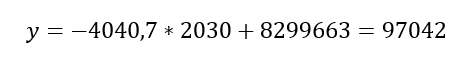
Vagyis az egyenletünk azt jósolja, hogy 2030-ban a győztes idő 97 042 másodperc lesz, azaz 1617,36 perc. vagyis 26,96 óra, azaz 1 nap és ~3 óra lesz, körülbelül ennyi kell majd a győzelemhez. 2018-ban A "Wild Oats XI" nevű hajó 1 nap 19 óra 7 perc és 21 másodperces időeredménnyel nyert, vagyis a következő 12 évben körülbelül 16 órával javulnak majd az időeredmények, ha minden a terv szerint halad.
Összefoglalás:
Számomra fantasztikus az a kitartó és magasszintű mérnöki munka, amely ezt a töretlen fejlődést eredményezte. Ne felejtsük el, hogy mindez 75 év kitartó munkájának köszönhető, vagyis valószínűleg nem egy, hanem legalább 2-3 nemzedék részvételét feltételezi. Bár nem vagyok vitorlás rajongó és nem is tudok vitorlázni, részemről megemelem a kalapom mindazok előtt, akik részt vettek és részt vesznek ennek a csodálatos teljesítménynek az elérésében.
A további bejegyzésekben egyrészt bemutatom majd, hogy hogyan kell elvégezni ugyanezt az elemzést a Minitab programmal, illetve azzal fogunk foglalkozni, hogyan tudunk meggyőződni arról, hogy mennyire jó a regressziós egyenesünk.
Források:





