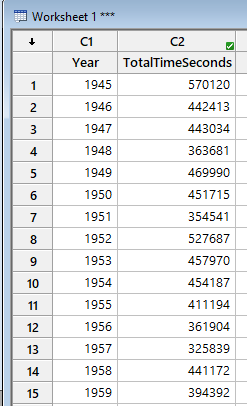
Az előző bejegyzésben (A Sidney – Hobart Yacht verseny – Szigorúan monoton fejlődés) részletesen bemutattam a regressziós egyenes egyenletének kiszámítását. Ezt a bejegyzést igen rövidnek szánom, hiszen a célom csak annyi, hogy bemutassam, hogy néz ki mindez Minitab-ban.

Annak ellenére, hogy elég sok karaktert pazaroltam el a lineáris regresszió magyarázatára, a fent említett példa igazából nem számít bonyolultnak a regresszió elemzés világában. A Minitab-ban is tulajdonképpen egyetlen menüpont elindításával elkészíthetjük az elemzésünket a már előre beadott adatsor alapján. Mielőtt belevágnánk a tesztbe, az adatainkat két oszlopba kell rendeznünk, amelyikből az egyik természetesen az x, a másik pedig az y változó értékeit tartalmazza. Jelen esetben ez természetszerűleg adódott, hiszen a Wikipédián talált eredeti táblázatban is így voltak elrendezve az adatok, csak ki kellett őket másolni a táblázatból és beilleszteni a Minitab adatmezőibe.

A próba legegyszerűbb végrehajtása az, ha a ’Stat’ menü ’Regression’ almenüjében kiválasztjuk a ’Fitted Line Plot’ parancsot.

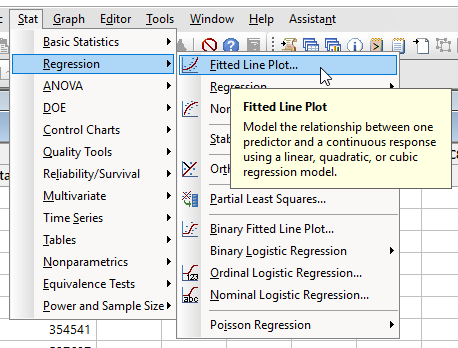
Azon persze lehetne rugózni, hogy miért nem az alatta lévő ’Regression’ parancsot kell kiválasztani és azon is, hogy ezt a ’Fitted Line Plot’-ot miért nem hívják például ’Simple Linear Regression’-nek, de ebbe most inkább mégsem mennék bele, igazából kezdek beletörődni, hogy én vagyok fordítva bekötve. Mindegy.

Szóval a parancsot elindítva természetesen most is megjelenik egy párbeszéd ablak, ahol meg tudjuk adni a teszt adatait. Tényleg nagyon egyszerű az egész, csak néhány nagyon egyszerű adatot kell megadnunk.

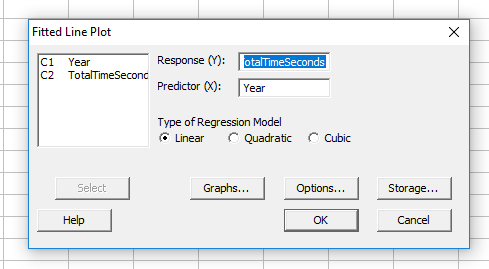
A legfontosabb az, hogy meg kell mondanunk a programnak, hogy melyik oszlopban találja az x és az y változókat, azaz melyik változót tegye a vízszintes és melyiket a függőleges tengelyre. A ’Type of Regression Model’ alatt válasszuk ki a ’Linear’-t, mert az előzetesen elkészített grafikonok alapján erősen sejtjük, hogy a két változó értékei között lineáris kapcsolat van.

A ’Graphs’ nyomógomb megnyomásával egy újabb ablak jelenik meg, ahol megadhatjuk, hogy a maradékok (Residuals) elemzésére milyen grafikonokat szeretnénk alkalmazni.

Én ezt a beállítást szoktam alkalmazni, mert a ’Standardized’ csak akkor kell, ha a maradékok nem normál eloszlásúak, a ’Deleted’ pedig egy speciális elemzés, amelyet a kiugró értékű maradékok elemzésére használunk. A grafikonok közül a ’Four in one’ a legpraktikusabb, mert így az összes grafikont egy helyen megtalálom.

Az ’Options’ nyomógomb hatására egy másik ablak jelenik meg, itt adat transzformációkat tudunk beállítani, illetve itt tudjuk megadni a teszt megbízhatósági szintjét is. A ’Display options’ alatt megadhatjuk, hogy a program rajzolja be a megbízhatósági (confidence interval) és a becslési tartományokat (prediction interval) vagy sem. Ezekről majd később…

A ’Storage’ nyomógomb megnyomásakor pedig beállíthatjuk, hogy a teszt mely számolt paramétereit tárolja el a program valamelyik cellatartományban. Ez akkor lehet praktikus, ha mondjuk a maradékokat tovább akarnánk elemezni más módszerekkel.

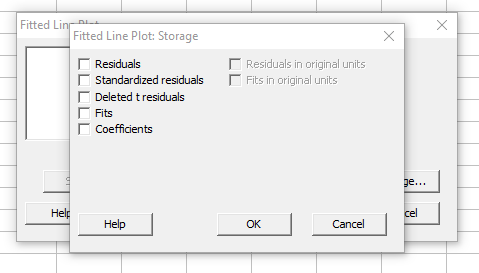
És végre eljutottunk oda, hogy megnyomjuk az ’OK’ gombot. Lássuk a végeredményt:

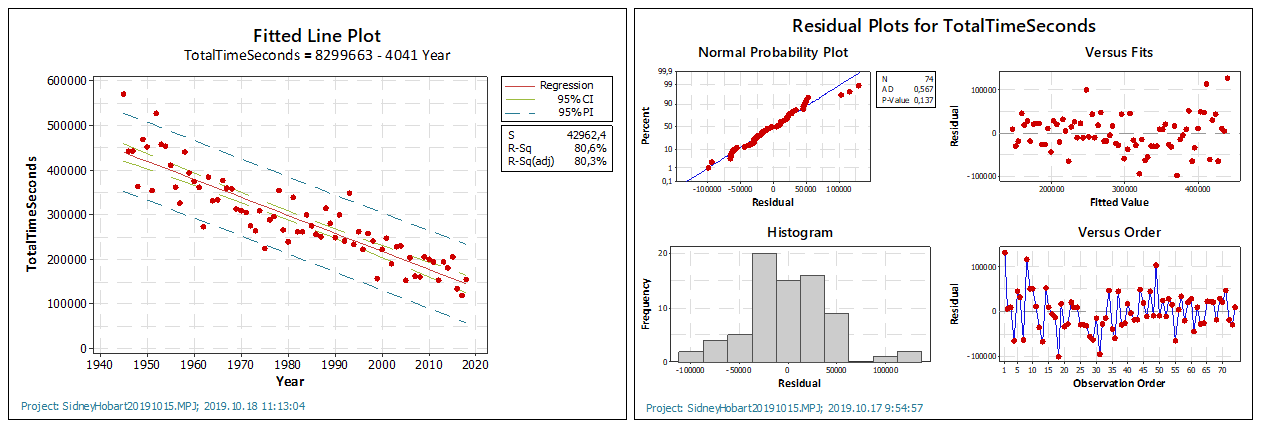
A Minitab a teszt összes eredményét összefoglalta két darab táblázatban, ami így teljesen jól értelmezhetővé vált, ha valaki tudja, hogy mit kell nézni. A bal oldali diagramon a már jól ismert scatter-diagram látható. Amiben ez több, hogy kétféle intervallum is be van jelölve rajta szaggatott vonalakkal:

A megbízhatósági intervallum (confidence interval) a regressziós egyenes körüli piros szaggatott vonal. Az alapelv hasonló, amint azt az átlag standard hibája esetében tapasztaltuk (Az átlag standard hibája). Mivel a regressziós egyenes az adatpontok átlagát becsüli a minta alapján, itt is ugyanazzal a problémával szembesülünk: Ha a minta átlaga egy adott szám, abból az következik, hogy a sokaság átlaga egy adott tartományon belül van, de hogy pontosan hol, azt nem tudjuk.

A becslési tartomány (Prediction interval) viszont azt mutatja meg, hogy a sokaság egyes pontjai mely tartományba fognak esni a regressziós egyenes körül (Hátrébb az agarakkal! – Mennyire hihető a regressziós egyenes becslése?).

A legfontosabb viszont az, hogy a diagram tetején a cím alatt megtalálható a regressziós egyenes becslése, ami miatt az egészet csináljuk. Aminek nagyon örülök, hogy a Minitab által adott becslés teljesen megegyezik azzal, amit korábban excelben kiszámoltam (Tudom, hogy gőzgép, de mi hajtja? – Egyváltozós lineáris regresszió – a regressziós egyenes meghatározása).

A másik diagram tulajdonképpen négy diagram kombinációja, amelyik mind az egyes adatpontoknak a regressziós egyenestől való eltéréseit (maradékok, vagy angolul residuals) mutatják meg különféle módokon. Ezeknek a grafikonoknak az értelmezését szintén meg lehet találni az előbb említett cikkben, úgyhogy ennek a részletezésétől most eltekintek.

Reménykedem benne, hogy mindenki számára világos és jól követhető volt ez a kis cikksorozat és sikerült barátságot kötni a regresszió elemzések legegyszerűbb tagjával. A későbbiekben azért még csavarok majd egyet ezen, de ez legyen a jövő zenéje, addig még jöjjön egy-két kevésbé fajsúlyos téma…