Két orvos próbálja eldönteni betegekről, hogy vajon skizofréniásak-e vagy sem. Az egyikük pszichológus, aki általában projektív technikákkal vizsgálja a betegeket, a másik pedig egy pszichiáter, aki inkább screening interjúk alapján dolgozik. Ilyen körülmények között érdemes feltenni a kérdést, hogy vajon a két orvos mennyire fog egyforma döntést hozni ugyanazokról a betegekről; vagyis, ha egy beteg az egyik orvos szerint skizofréniás, akkor a másik orvos is ugyanerre a következtetésre fog-e jutni vagy sem.

Hasonló probléma, amikor egy gyárban ugyanazt a terméket több különböző ellenőr is ellenőrzi; vajon mindegyik ellenőr ugyanazt a döntést hozná meg az ellenőrzött termékekről? Az ellenőrzés módszere mennyire biztosítja azt, hogy a jó darabok mindig jónak lesznek ítélve, a rosszak pedig rosszaknak, függetlenül attól, hogy ki ellenőrizte őket? Lehetséges-e ezt mérni? Jellemezhető-e valamilyen mérőszám segítségével az, hogy két értékelő személy mennyire dönt egyformán olyan esetekben, amikor a döntésnek két lehetséges kimenetele van?

A hasonló problémákra próbált megoldást találni Jacob Cohen matematikus, amikor 1960-ban közzétette a Cohen-féle kappa tesztről szóló tanulmányát (lásd a cikk végén). A publikáció nagy része kivételesen egészen jól érthető, Cohen elmagyarázza az egész problémakör hátterét.

Amikor két kiértékelő személy döntést hoz ugyanazokról a dolgokról vagy jelenségekről, első látásra nem tűnik annyira bonyolultnak kiszámítani, hogy mennyire döntenek egyformán. Ha feltesszük, hogy a döntéseknek csak két lehetséges kimenetele lehet (pl.: igaz vagy hamis), akkor a döntéseiknek összesen négyféle lehetséges kimenetele van:

• Mindkét kiértékelő személy úgy dönt az adott dologról, hogy igaz,
• Mindkét kiértékelő személy úgy dönt az adott dologról, hogy hamis,
• Az első kiértékelő személy úgy dönt, hogy a dolog igaz, a másik kiértékelő személy viszont úgy dönt, hogy a dolog hamis,
• Az első kiértékelő személy úgy dönt, hogy a dolog hamis, a másik kiértékelő személy viszont úgy dönt, hogy a dolog igaz.

Az egyszerű megközelítés az, hogy összeadjuk azoknak az eseteknek a számát, amikor a két kiértékelő személy azonos módon dönt, azaz mindkettő úgy dönt, hogy a dolog igaz, vagy úgy, hogy a dolog hamis. Ha ezt elosztjuk az összes eset mennyiségével, akkor megkapjuk azt a százalékos arányt, amely azt jellemzi, hogy a két kiértékelő személy mennyire dönt egyformán. Igen, de sajnos ezzel van egy kis gond!

Mégpedig az, hogy ez a fenti arány azokat az eseteket is tartalmazza, amikor az ellenőrök döntéseit a véletlen befolyásolja! Na ja, de mit jelent az, hogy a döntéseiket a véletlen befolyásolja? Képzeld el azt az esetet, amikor a két döntnöknek mondjuk 100 esetben kellene eldöntenie, hogy melyik eset igaz és melyik hamis. A két döntnök fog egy-egy érmét, és elkezdik feldobálni a levegőbe. A száz eset már elég nagy szám ahhoz, hogy az érmék az esetek egy részében azonosan döntsenek! Mivel csak négy különböző döntési helyzet lehetséges és az érmék esetében a fej és az írás valószínűsége egyformán 50%-50%, ezért a négyféle döntés valószínűsége egyformán 25%-25%! (A binomiális eloszlás - lépjünk szintet az érmedobálásban)

Vagyis a véletlen még akkor is jelentősen befolyásolja a két kiértékelő személy döntéseit, ha egyébként ők tudatosan, a szabályok betartásával végzik el a feladatukat! A probléma az, hogy adott esetben nehezen választható szét az, hogy egy adott esetben az egyezőség a kiértékelő személyek tudatos döntése, vagy csak a véletlen műve. Jacob Cohen pontosan ezt a problémát oldotta meg azáltal, hogy kidolgozta a Kappa-tényezőt, hiszen

The coefficient Kappa is simply the proportion of chance-expected disagreements which do not occur, or alternatively, it is the proportion of agreement after chance agreement is removed from consideration

azaz

A Kappa-tényező egyszerűen a véletlen miatt elvárt véleménykülönbségek aránya, amelyek nem történtek meg, vagy másképpen fogalmazva az egyforma döntések aránya azután, hogy a véletlenszerű egyetértéseket eltávolítottuk az elemzésből

Nézzük meg mindezt egy példán keresztül. Tegyük fel, hogy két ellenőr ellenőrzi ugyanazt a 12 terméket és el kell dönteniük, hogy a termékek jók vagy nem. Ha a termék jó, akkor az ellenőrök IGEN-nel döntenek, ha pedig hibás, akkor NEM-mel. Az alábbi táblázat tartalmazza az ellenőrök döntéseit. 5 esetben mindkét ellenőr IGEN-nel és 4 esetben mindkét ellenőr NEM-mel döntött. 2 esetben az első ellenőr IGEN-nel döntött, de a második ellenőr NEM-mel, illetve 1 esetben az első ellenőr NEM-mel döntött és a második IGEN-nel.

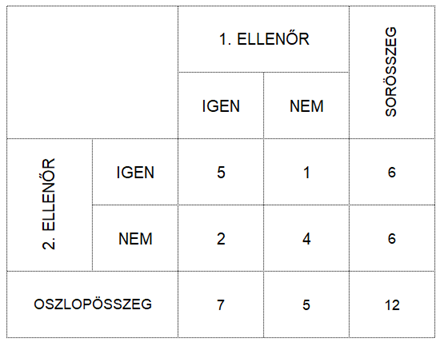
Ha a cikk elején említett egyszerű százalékszámításos módszert alkalmazzuk, akkor a következőt kapjuk:

Eddig jó, de hogyan vesszük ebből ki azt a részt, amelyet a véletlen okoz? Egy korábbi cikkben (Gyakoribb-e a kék szem a szőkék között? – Khí-négyzet próba a függetlenség vizsgálatára) már foglalkoztam azzal a témával, hogy mikor mondjuk azt két valószínűségi változóra azt, hogy ezek viselkedését csak a véletlen befolyásolja. Akkor, ha a két valószínűségi változó független egymástól; vagyis, ha ezek értékei semmilyen módon nem függenek egymástól. Ez pedig akkor fordul elő, ha a két valószínűségi változó együttes előfordulási valószínűsége megegyezik a két valószínűségi változó külön-külön előfordulási valószínűségeinek összegével! Ha ezt valahogyan ki tudnánk számolni és ki tudnánk vonni Po-ból (Pobserved, azaz Pészlelt), akkor már meg is lenne a megoldás.

Nevezzük el ezt a véletlentől függő valószínűséget Pc-vel (az angol „chance” szó után, amelyet Cohen igen gyakran használt a tanulmányában a véletlen megnevezésére). Nos, ezt a Pc-t nagyon hasonlóan számoljuk ki, mint ahogyan azt a fentebb hivatkozott cikkben tettük.

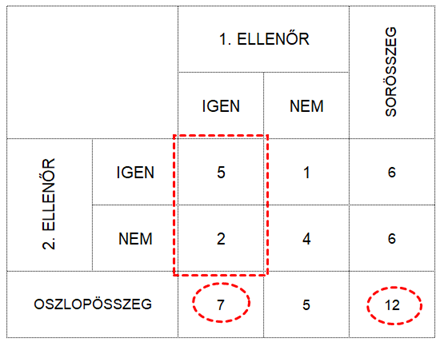
Ha a két ellenőr döntése teljesen független lenne egymástól (ez esetben persze reméljük, hogy nem az), akkor annak a valószínűsége, hogy mindkét ellenőr IGEN-t dönt, megegyezne a két egyedi esemény szorzatával. Annak a valószínűsége, hogy az 1. ellenőr IGEN-t dönt, jelen esetben 7/12, vagyis 0,58, hiszen az 1. ellenőr 7 esetben döntött IGEN-nel a 12-ből. Itt most lényegtelen, hogy a 7-ből két esetben másként döntött, mint a 2. ellenőr, az a fontos, hogy ő 7 esetben döntött IGEN-nel.

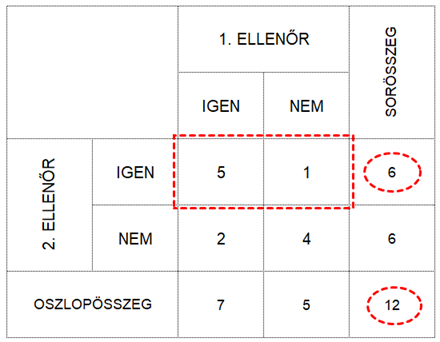
Ugyanígy a 2. ellenőr 6 esetben döntött IGEN-nel, vagyis az ő döntésének a valószínűsége 6/12, azaz 0,5.

Vagyis annak a valószínűsége, hogy mind a két ellenőr IGEN-nel szavazna, ha a döntéseik függetlenek lennének egymástól, az 0,58*0,5=0,29.

Hasonlóképpen ki kell számolnunk annak a valószínűségét, hogy mindkét ellenőr NEM-mel szavaz, hiszen ez is része Po-nak. Az 1. ellenőr 1+4=5 esetben döntött NEM-mel, azaz ennek a valószínűsége 5/12, azaz 0,416.

A 2. ellenőr ismét 6 esetben hozott nemleges döntést a 12-ből, ami ismételten 0,5.

Ez alapján annak a valószínűsége, hogy mind a két ellenőr NEM-mel fog dönteni, 0,416*0,5=0,21. Annak a valószínűsége, hogy mindkét ellenőr IGEN-nel vagy mindkét ellenőr NEM-mel döntene, ha a döntéseik csak a véletlentől függenének:

Eddig szuper, mert sikerült kiszámítanunk, hogy a két ellenőr döntéseinek mekkora része függ pusztán a véletlentől. Ha ezt kivonjuk Po-ból, akkor azt kapjuk, hogy

És ez így már nem is néz ki olyan jól, hiszen ebben az esetben az látszik, hogy a két ellenőr csak 25% eséllyel dönt TUDATOSAN egyformán, ami viszont egy elég gyenge valószínűség. Észrevehető, hogy milyen jelentős az eltérés a kétféle módszer között, ez esetben a két ellenőr működését a véletlen erősen befolyásolja.

Cohen azonban nem elégedett meg ennyivel, ő szeretett volna egy - a Pearson-féle korrelációs együtthatóhoz (Valaki átírta a korrelációs együttható képletét, hogy ne lehessen érteni? Ez most komoly…?) hasonló – korrelációs tényezőt létrehozni, ezért a fenti különbséget még elosztotta 1-Pc-vel, ami ugye megfelel a tudatosan hozott összes döntés valószínűségének, hiszen ebben mind a négy döntési variáció valószínűsége benne van, mert a véletlen hatását kivontuk 1-ből. Végül az így kiszámított tényezőt elnevezte Kappának:

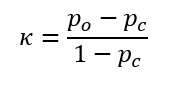
Természetesen Cohen bebizonyítja, hogy a Kappa-tényező értéke csak -1 és +1 között változhat, amelyet úgy értelmezhetünk, hogy ha Kappa közel van a +1-hez, akkor a két kiértékelő személy nagyon egyformán dönt, ha 0 körül van az értéke, akkor a két kiértékelő személy döntései közel függetlenek egymástól, ha pedig -1 körüli értéket kapunk, akkor a két kiértékelő személy szinte teljesen ellentétesen dönt.

A két értékelő személy döntéseinek egyformaságát egyébként Landis és Koch határozta meg a következő módon. Ha Kappa nagyobb nulla, akkor

0 < Kappa < 0,2                -            Nincs összefüggés a két értékelő személy döntései között

0,21 < Kappa < 0,4          -             Kis összefüggés van az értékelő személyek döntései között

0,41 < Kappa < 0,6          -             Közepes összefüggés van az értékelő személyek döntései között

0,61 < Kappa < 0,8          -             Erős összefüggés van az értékelő személyek döntései között

0,81 < Kappa < 1              -            Majdnem tökéletes összefüggés van az értékelő személyek döntései között

Más megközelítések szerint a két értékelő személy döntései akkor elfogadhatók, ha Kappa értéke nagyobb, mint 75%.

A Cohen-féle Kappa tesztnek vannak korlátai, az egyik legfontosabb, hogy csak két értékelő személy döntéseinek összehasonlítására alkalmas, három, vagy több személyre nem alkalmazható, erre a Fleiss-féle Kappa-tesztet alkalmazhatjuk, ezt a következő bejegyzésben fogom bemutatni.

Frissítés 2021 október 29-én:

A Cohen-féle kappa teszt végrehajtásakor ügyelni kell arra, hogy csak akkor fog kijönni értékelhető eredmény, ha a vizsgált minták között vannak jó és rossz darabok is. Amennyiben nincs olyan minta, amelyet mindkét ellenőr elutasít, akkor kappa értéke 0 lesz!

Források:

Jacob Cohen: A COEFFICIENT OF AGREEMENT FOR NOMINAL SCALE, EDUCATIONAL AND PSYCHOLOGICAL MEASUREMENT, VOL. XX, No. 1, 1960 https://www.semanticscholar.org/paper/A-COEFFICIENT-OF-AGREEMENT-FOR-NOMINAL-SCALES-1-Cohen/9e463eefadbcd336c69270a299666e4104d50159

Landis JR, Koch GG. The measurement of observer agreement for categorical data. Biometrics. 1977;33(1):159–74. https://www.ncbi.nlm.nih.gov/pubmed/843571