Egy korábbi cikkemben (Mennyire döntünk egyformán? – A Cohen-féle Kappa teszt) már tisztáztuk a Cohen-féle Kappa teszt lényegét és elvégzésének módját. Sajnos azt is tisztáztuk, hogy ennek a tesztnek van két szigorú korlátja:

• csak két kiértékelő személy esetén alkalmazható.
• csak két döntési kritériummal rendelkező, vagyis IGEN-NEM típusú döntések esetén alkalmazható.

A fenti gyengeségek orvoslására több megoldást is kitaláltak, ebből szeretnék most egyet bemutatni.

Ez a Fleiss-féle Kappa teszt, amelyet kifejezetten arra találtak ki, hogy kettőnél több ellenőr döntéseinek egyezőségét vizsgálja. Ezt a megoldást Joseph L. Fleiss, egy amerikai professzor publikálta 1971-ben. A módszer bevallottan a Cohen-féle Kappa teszt fent említett gyenge pontjaira keresett megoldást. Érdekessége, hogy az alapkoncepciója tulajdonképpen ugyanaz, mint a Cohen-féle teszté, vagyis a Fleiss-féle teszt is szétválasztja a tudatos és a véletlenszerűségből adódó döntéseket. Még a Kappa-tényező kiszámítása is ugyanazzal a képlettel történik, mint a Cohen-féle Kappa esetében:

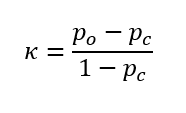
ahol,

Po – az értékelő személyek tudatos döntéseiből származó egyezőségek valószínűsége (Pobserved, azaz Pészlelt),

Pc – a véletlenszerűségből adódó egyezőségek valószínűsége (Pchance, azaz Pvéletlen).

A Kappa-tényező is ugyanúgy -1 és +1 között változik, és a döntések egyezőségét is hasonlóan értékeljük ki, mint a Cohen-féle Kappa esetében. A valószínűségeket viszont másképpen értelmezzük és számítjuk, mert más a teszt szituáció. Ebben az esetben nem két ellenőrünk van (lehet csak kettő is), hanem tulajdonképpen akármennyi lehet. A vizsgált esetekben a döntések eredménye is lehet többféle, nemcsak kettő.  De ezt egy példán jobban tudom szemléltetni. A módszer az egészségügyből származik, de én mérnökként dolgozom és egy iparból vett példát jobban magam elé tudok képzelni.

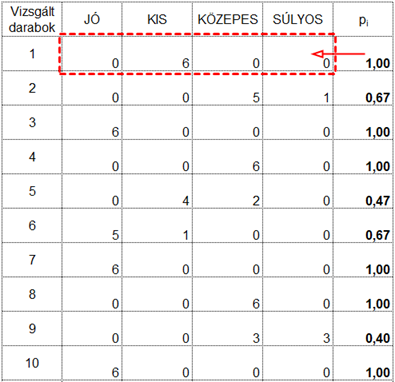
Tegyük fel, hogy egy termék vizuális ellenőrzését kell elvégeztetnünk több ellenőrző személlyel és az a célunk, hogy olyan ellenőrzési módszert és kiértékelési folyamatot határozzunk meg, amellyel biztosítani tudjuk, hogy az ellenőrzést végző dolgozók lehetőleg minél biztosabban tudják megkülönböztetni e különböző hibákat. Jelen esetben az ellenőrzött termékeket nemcsak két csoportba lehet osztani, úgymint jók és rosszak, hanem a hibák között meg lehet különböztetni KIS, KÖZEPES és SÚLYOS hibákat. A vizsgálati eljárás tesztelése céljából kiválasztunk 10 terméket, amelyek között természetesen vannak JÓ, KIS, KÖZEPES és SÚLYOS hibával rendelkező termékek is. Ezek után az összes terméket leellenőriztettük az összes ellenőrrel (a módszer érdekessége, hogy ez sem kötelező, a szisztéma úgy is működik, ha nem minden ellenőr hoz döntést minden esetről), majd az eredményeket összegyűjtöttük a következő táblázatban:

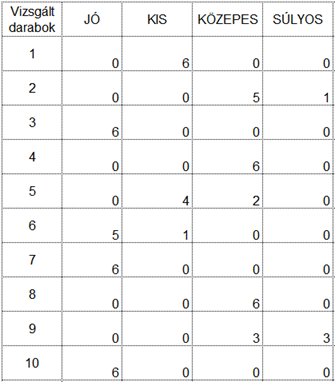
A táblázat sorai tartalmazzák a vizsgált darabokat, az oszlopok pedig a lehetséges döntéseket. A táblázat egyes mezőiben pedig az ellenőrök által hozott döntések vannak; azaz, hogy hány ellenőr hozott egy adott döntést egy adott darabról. Például az első darabot mind a hat ellenőr kis hibásnak ítélte meg. A második darabot 5 ellenőr közepesen hibásnak látta, 1 ellenőr pedig súlyosan hibásnak ítélte meg. Az alapkérdés tehát ugyanaz marad; mennyire döntenek az ellenőrök egyformán?

Ez esetben is valószínűségekről beszélgetünk, azonban itt a valószínűségszámítás nyelvére lefordítva az a kérdés, hogy ha egy ellenőr mondjuk az első esetben eldöntötte, hogy a vizsgált termék jó, akkor mekkora a valószínűsége annak, hogy egy véletlenszerűen kiválasztott másik ellenőr is ugyanígy fog dönteni. Mivel mindig két ellenőr döntését hasonlítjuk össze, ezért egy adott eset vizsgálatakor az ellenőrpárok száma mindig meg fog egyezni azzal, ahányszor egy ellenőrpárt ki tudunk választani. Vagyis mindig két ellenőrt választunk ki függetlenül attól, hogy hány ellenőr döntéseit vizsgáljuk. Korábban viszont már megtanultuk (Székfoglaló, avagy egy kis kombinatorika…), hogy ha n darab gyereket próbálunk k darab székre leültetni, akkor n-től kezdve (n-k+1)-ig csökkenő sorrendben össze kell szoroznunk a számokat. Mivel itt k mindig 2, ezért n értékétől függetlenül mindig n(n-1) esetünk lesz.

Jelöljük a vizsgált darabok számát N-nel, az ellenőrök számát n-nel, a kategóriák számát, amelybe be lehet osztani a vizsgált darabokat pedig k-val. i-vel fogjuk jelölni a vizsgált darabok sorszámát és j-vel jelöljük majd az ellenőrök sorszámát.

Mivel ebben a példában minden ellenőr minden egyes darabot megvizsgált, ezért minden darab 6 darab vizsgálaton esett át. Tegyük fel, hogy az első darabot az első ellenőr a kis hiba kategóriába helyezte el. Mekkora a valószínűsége annak, hogy egy másik ellenőr is kis hibásnak fogja értékelni a terméket? Mivel a tesztünk során mind a hat ellenőr kis hibát észlelt, ezért annak a valószínűsége, hogy hat ellenőrből kettőt ki tudunk választani, 6x5=30 lesz. Mivel a terméket egyetlen ellenőr sem sorolta egyetlen más kategóriába sem, azért ezzel a darabbal egyelőre végeztünk.
Nézzük a második darabot: A második darab esetében 5 ellenőr közepesnek, 1 pedig súlyosnak ítélte meg az észlelt hibát. A közepes hiba esetében 5 ellenőrből kettőt 5x4=20 féle módon tudjuk kiválasztani, a súlyos hiba esetében viszont ez 0 lesz, hiszen ezt a kategóriát csak 1 ellenőr választotta ki, így 0 a valószínűsége annak, hogy egy második ellenőr is ezt fogja választani.
Az átlag kiszámításához szükségünk van arra, hogy egy adott esetben hány ellenőr párunk van maximálisan. Nos, egy adott darab esetében – ahogy azt már az első darabnál láttuk – 6x5=30 lehetőség van. Egy kicsit általánosabban egy adott darab esetében annak az átlagos valószínűsége, hogy egy adott ellenőr után egy másik ellenőr is az adott kategóriába fogja sorolni a terméket, az a következő módon néz ki:

Rendezgessük ezt át egy picit! Először is szorozzuk be nij-vel a zárójelen belüli kivonást:

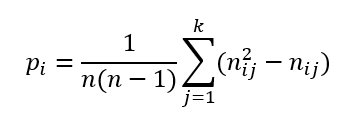
Ha nij-t kiemeljük a szummából, akkor viszont a következőt kapjuk:

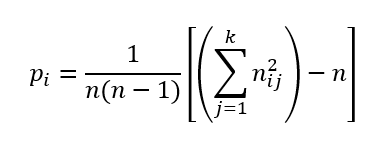
Természetesen Pi egy adott termék döntéséhez tartozó valószínűség, így annak a valószínűsége, hogy az ellenőrök mind a 10 esetben azonosan fognak dönteni, az egyedi Pi valószínűségek átlaga lesz.

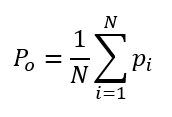
Pc kiszámításakor annak a valószínűsége, hogy bármelyik kiválasztott ellenőr a vizsgált terméket egy adott kategóriába fogja tenni egyenlő és megegyezik Pj-vel. Ha két ellenőr egymástól függetlenül dönti el, hogy az adott termék a kiválasztott kategóriába tartozik, akkor ennek a valószínűsége megegyezik a két ellenőr döntés valószínűségének szorzatával, azaz Pj négyzetével. Így

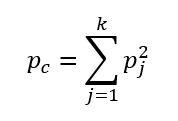
Mivel Po és Pc értékét is ki tudjuk számolni, így ezeket a cikk elején bemutatott képletbe behelyettesítve ki tudjuk számolni Kappa értékét. Nos, végére értünk a hieroglifáknak, nézzük meg a Kappa statisztika működését a fenti egyszerű példán. Tehát a kiinduló táblázatunk ugyanaz, mint fent:

Kezdjük a feladat megoldását Pi értékeinek kiszámításával. Egy új oszlopban a fenti képlet alapján minden egyes vizsgált darabhoz kiszámoltam Pi értékét a következő képlettel:

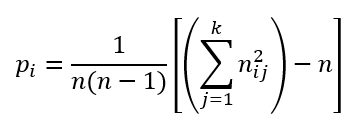
Táblázatkezelői nyelvre lefordítva a táblázat első sora a következő módon számolható ki:

=(1/(6*5))*((B2*B2+C2*C2+D2*D2+E2*E2)-6)

Fontos, hogy a második zárójelen belülről nem szabad elfelejteni kivonni az ellenőrök számát, azaz 6-ot.

Ezután számítsuk ki, hogy melyik kategóriába hány döntés jutott.

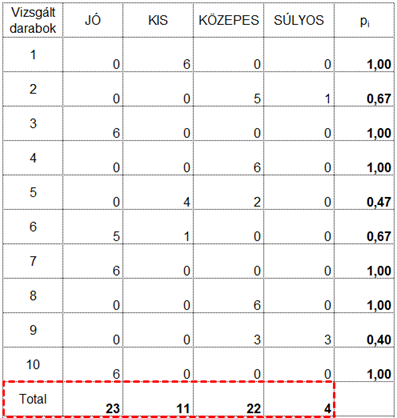
Az oszlopösszegek alapján ki tudjuk számolni minden kategóriához, hogy átlagosan hány ellenőr választotta az adott kategóriát, azaz Pj értékét. Itt arra kell ügyelni, hogy az átlag kiszámítása során a Total-t az adott kategóriára eső ellenőrzések maximális számával kell elosztani (jelen esetben van 6 ellenőr, akik 10 darab terméket ellenőriznek, ez így 6x10=60). A sor végén pedig az oszlopátlagok négyzetösszege szerepel, amely a fentebb említettek alapján megadja Pc értékét.

A Pi oszlopban szereplő értékek átlaga fogja megadni Po-t, A Pj sor végén lévő négyzetösszeg pedig megadja Pc-t.

Így mindkét adatunk megvan Kappa kiszámításához, tehát

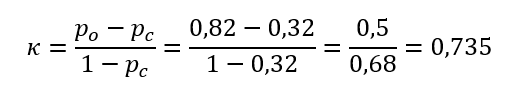
Jelen esetben a 10 darabból 3 esetében nem döntöttek azonosan az ellenőrök, így szerintem az eredményként kapott 73,5% körülbelül tükrözi a helyzetet, vagyis a Landis és Koch szerinti skála alapján (lásd a Cohen-féle Kappáról szóló bejegyzést) erős összefüggés van az ellenőrök döntései között, de például a hivatalos MSA-kézikönyvben megadott minimum 75%-os követelmény alatt van, így az ellenőrzési módszer még fejlesztésre szorul.

Tudom, hogy a cikk eleje egy kicsit nehezen emészthető, de azért remélem, hogy követni lehetett a gondolatmenetet, illetve hogy a gyakorlati példa alapján bárki el tud készíteni táblázatkezelőben, vagy akár kézzel is egy hasonló elemzést.

Források:

Wikipédia – Fleiss’ Kappa test
https://en.wikipedia.org/wiki/Fleiss%27_kappa

Joseph L. Fleiss: Measuring nominal scale agreement among many raters, Psychological Bulletin, 1971, Vol 76., No. 5, 378-382
http://www.wpic.pitt.edu/research/biometrics/Publications/Biometrics%20Archives%20PDF/395-1971%20Fleiss0001.pdf