Ismét sikerült számomra idegen területre tévednem, de egy kedves olvasó megkeresett privátban, hogy segítsek neki néhány befektetésekkel kapcsolatos mérőszám értelmezésében. Némi diskurzus után elérkeztünk a részvények béta mutatójához és megpróbáltuk közösen értelmezni, hogy ez mit is jelent tulajdonképpen.

Az interneten számtalan forrás létezik, amely bemutatja a béta mutatót, sőt még a kiszámításához használt képletet is feltüntetik hozzá, de ahogy azt már megszokhattuk a statisztikában, a lényeg valahol megint csak elsikkadt a sok egyszerűsítés közepette.

Szóval, mi is ez a béta mutató?

Néhány idézet a fent említett forrásokból a teljesség igénye nélkül:

„A béta mutató fejezi ki egy részvény kockázatosságát egy indexhez viszonyítva. Azaz azt mutatja meg, hogy az egyedi részvény mennyivel volatilisebb a piachoz képest.”

/elemzeskozpont.hu/

„Ezért adekvát mérőszáma a hosszú távú befektetőnek a béta, amely azt fejezi ki, hogy a piaci portfolió árfolyamának 1%-os változását az adott részvény hány százalékos árfolyam-változása kíséri.”

/Vincze László: Tőkepiaci ismeretek/

„Beta is a measure used in fundamental analysis to determine the volatility of an asset or portfolio in relation to the overall market.”

/Investopedia/

„A measure of a security's sensitivity to movements in the overall market”

/CFI/

A béta mutató kiszámítására a következő képletet szokták szerepeltetni:

vagy

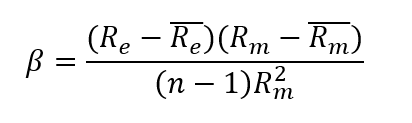
ahol

Re – a vizsgált befektetési eszköz varianciája

Rm – a piac varianciája, amelyhez az adott befektetési eszközt viszonyítjuk

És itt valahogy teljesen elvesztettem a fonalat. Hogy jön ide a kovariancia és ha már normalizáljuk a kovarianciát, akkor miért nem a piac szórásával osztjuk el, miért a varianciájával? Szóval szerény statisztikai ismereteim birtokában mind a definíciók, mind pedig a képlet teljesen értelmetlennek tűnt.

Mindaddig, amíg valahol azt nem olvastam, hogy a dolognak köze van a regresszióhoz, mert ekkor elkezdett megvilágosodni a dolog. Hiszen én erről már írtam egy cikket (Tudom, hogy gőzgép, de mi hajtja? – Egyváltozós lineáris regresszió – a regressziós egyenes meghatározása), és ott már bemutattam, hogy lineáris regresszió esetében – amikor az adatpontok egy egyenesre illeszthetők rá adott pontatlansággal – a regressziós egyenest a következő módon írjuk fel:

A befektetések esetében is két fontos vonatkozó mutatót alkalmaznak a szakemberek, az alfát és a bétát. És tényleg, ha így írjuk fel, akkor mindjárt egy fokkal élesebb lesz a kép:

Azt azért kiemelném, hogy ez az alfa nem egyezik meg azzal az alfával, amelyet a befektetési iparban annak hívnak. Az alfa ez esetben az egyenes metszéspontja az y-tengellyel, a béta pedig az egyenes meredeksége (lásd a fent említett blogbejegyzést).

Tovább folytatva a fenti okfejtést, a fentebb belinkelt blogbejegyzésben azt is bemutattam, hogy az egyenes meredekségét a következő módon számoljuk ki:

vagy jelen esetben

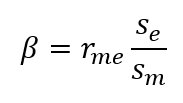
ahol

rme – a vizsgált befektetési eszköz és a piac korrelációs együtthatója

se – a vizsgált befektetési eszköz szórása

sm – a piac szórása

A korrelációs együtthatóról viszont egy másik blogbejegyzésben ejtettem szót (Valaki átírta a korrelációs együttható képletét, hogy ne lehessen érteni? Ez most komoly…?) és itt részletesen bemutattam a korrelációs együttható kiszámításának módját és értelmezését. A képlet a következőképpen néz ki:

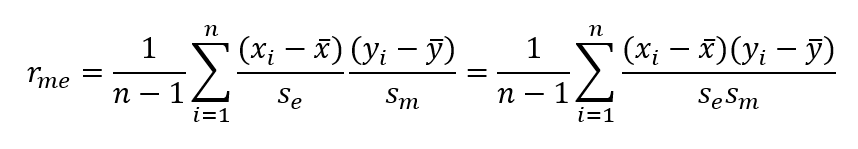
ahol

xi – a vizsgált befektetési eszköz i-dik időszakban tapasztalt ára

x̅ - a vizsgált befektetési eszköznek az n időszakra vonatkozó átlagára

yi – a piac i-dik időszakban tapasztalt ára

y̅ - a piac n időszakra vonatkozó átlagára

se – a vizsgált befektetési eszköz szórása

sm – a piac szórása

Ezt a képletet már csak vissza kell helyettesíteni béta képletébe és egy kicsit rendezkedni és se-vel egyszerűsítve meg is kapjuk a fent szerepeltetett béta képletet:

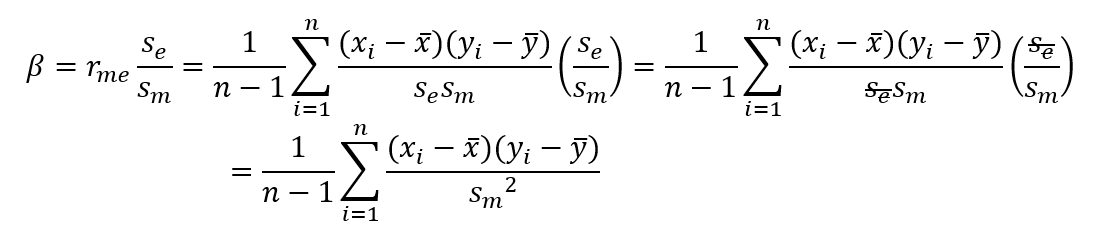
Mivel a vizsgált befektetési eszköz és a piac kovarianciája (és itt újra hivatkoznék a korábban belinkelt korrelációval kapcsolatos cikkre), …

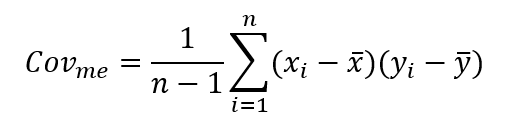
… így meg is kapjuk a keresett béta képletét, azaz

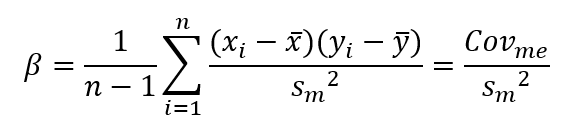
Nos, mi ebből a tanulság? Több is van. Például, hogy ez esetben a képlet végletes leegyszerűsítése ismét nem volt szerencsés ötlet, mert a kovariancia ez esetben semmilyen jelentéssel nem bír, tulajdonképpen csak egy algebrai egyszerűsítés eredménye, a nevezőben szereplő variancia pedig megint csak félrevezető, ha valaki nem ismeri a béta jelentésének történetét.

Ily módon értelmet nyer az egyik fenti definíció is, hiszen a béta tényleg azt adja meg, hogy a piaci ár 1%-os változása esetében a vizsgált eszköz ára hány százalékkal fog változni. Minél nagyobb lesz béta értéke egy részvény vagy más instrumentum esetében, annál nagyobb lesz az árváltozás, ha a piac valamilyen irányba megmozdul.

Van azonban még más tanulság is. Ha ebből a szempontból vizsgálunk mondjuk egy részvényt, hogy milyen összefüggés van mondjuk a BUX (magyar részvény esetén) vagy a SP500 (amerikai részvény esetén), akkor nem elég a puszta képlet alkalmazása, az is nagyon fontos, hogy a kétféle árra ráfektetett regressziós egyenes mennyire pontosan tükrözi vissza a két ár kapcsolatát (Hátrébb az agarakkal! – Mennyire hihető a regressziós egyenes becslése?). Ezen felül azt is érdemes megvizsgálni, hogy a vizsgált részvény és a részvényindex kapcsolata mennyire lineáris; mert, ha nem az, akkor a lineáris regresszióra vonatkozó törvényszerűségek nem, vagy csak nagyon korlátozottan alkalmazhatók az adott részvény esetében.

Vagyis, ha én figyelembe venném az adott részvény béta mutatóját a kereskedési döntésemben, akkor nemcsak szimplán megnézném valahol a kiszámított béta mutatót, hanem ténylegesen megvizsgálnám az adott részvény és a részvényindex közötti összefüggést, ábrázolnám a kétféle árat egy scatter-diagramon, elvégezném a regresszió elemzést és vizsgálnám azt is, hogy a regressziós egyenes mennyire pontosan írja le a kétféle ár közötti összefüggést.

Ihletet merítve a fentiekből, a következő cikkben el fogom készíteni egy konkrét részvény elemzését, ahogy én gondolom.

-----------------------------------------------

Dávid, kösz az ihletet,

dobom a bífszteket… :-)