A Rothamsted kísérleti állomás (Rothamsted Experimental Station) a világ legelső mezőgazdasági kutatóállomása. Az állomást 1843-ban alapította John Bennet Lawes és Sir Henry Gilbert, a Rothamsted Majorság tulajdonosa. A területen már korábban is végeztek különféle mezőgazdasági jellegű kutatásokat, a kísérleti állomás alapításának elsődleges célja pont ezen kutatások folytatásának biztosítása volt. A kutatások legfontosabb területe a foszfát-alapú műtrágyák hatásának vizsgálata volt a haszonnövények növekedésére.

Történetünk valójában 1919-ben kezdődött, amikor John Russel, a kutatóállomás akkori igazgatója felkérte Ronald Fischert, hogy segítsen kielemezni azt a hatalmas adatmennyiséget, amely a korábbi kutatások (Classical Field Experiments) során összegyűlt. A kísérletekről 1852-től kezdve álltak rendelkezésre adatok. A kísérleteket nagy, egybefüggő földterületeken végezték el és például a különféle talajoknak a terméshozamokra gyakorolt hatását úgy próbálták meghatározni, hogy az adott műtrágyát az egyik évben az egyik földön, a másik évben egy másikon próbálták ki. Mivel a fentebb felsorolt tényezők térben és időben folyamatosan változtak, az időjárás évenkénti változékonysága és a művelés módjában meglévő különbségek miatt az évről évre kapott eredmények nem voltak összemérhetők.

Ennek eredményeként a rendelkezésre álló 13 földterület művelési módja többször is változott a vizsgált körülbelül 70 éves időszak alatt. Az eredményeken észlelt változásokat 3 fő kategóriába lehetett sorolni:

• Évenkénti változások
• A talaj eróziója miatti stabil változások
• Olyan lassú változások, amelyek nem a talajminőség romlása miatt következtek be

Fischer 1921-ben adta közre első eredményeit a Studies in crop variation című írásában, amelyben részletesen – táblázatokban és diagramokon - összegzi és elemzi az összegyűlt adatokat. Ezen felül részletesen bemutatja az adatok elemzésének matematikai hátterét, amelyben olyan fogalmakat és eszközöket vezetett be, mint például a többváltozós regresszió (polynomial fitting), vagy az észlelt variancia tényezőkre bontása (Distrinution of variance for unchanging series of independent values), amelyeket mind a mai napig használnak a tudományos kutatásban. A tanulmány harmadik részében Fischer részletesen bemutatja az eredményeket, amelyeket a fentebb bemutatott matematikai módszerek alkalmazásával elért. Az összegzésben kiemeli azonban, hogy

„… egy hosszabb időtávon évről évre megfigyelt átlagos búza terméshozamok még az azonos földterületen azonos évszakban megtermelt gabona esetében sem hasonlíthatók össze. …”

A tudósok legnagyobb problémája az volt, hogy a rengeteg összegyűlt adat alapján nem sikerült konkrétan megítélni a vizsgált műtrágyák hatásait. egyszerűen túl sok tényező együttes hatását kellett felmérni, kezdve az elültetett haszonnövény fajtájától, a talaj minőségén keresztül a hőmérsékleti viszonyok változásáig és a csapadék mennyiségéig, illetve a művelésből adódó különbségekig. És még sorolhatnám…

Ennek megoldására találta ki Fischer a randomizálás módszerét. Ez annyit jelentett, hogy a korábbi gyakorlat helyett Fischer egy előre megadott kísérletterv alapján kis parcellákra osztotta fel az egyes földterületeket (lásd a fenti képet), amelyeknél azt is megadta előre, hogy melyik parcellára milyen növényt ültessenek, ezt milyen műtrágyával kezeljék, illetve hogyan kezeljék a talajt az ültetés előtt és alatt. Fischer a Latin-négyzet alkalmazásával osztotta fel a kísérleti földterületeket kis parcellákra.

A latin négyzet egy olyan ’n’ sorból és ’n’ oszlopból álló – azaz négyzet alakú – táblázat vagy mátrix, amely ’n’ különböző elemet tartalmaz úgy, hogy minden egyes elem csak egyszer fordulhat elő soronként és oszloponként. Vagyis majdnem olyan, mint egy sudoku…

Nézzük meg, mit is jelent ez egy példán keresztül. Tegyük fel, hogy 6 különféle kezelési mód hatásait szeretnénk összehasonlítani. Ekkor egy adott földterületet (amely nem szükségszerűen négyzet alakú) osszunk fel 36 körülbelül egyforma parcellára. a hatféle kezelési módot (A, B, C, D, E és F) el tudjuk úgy osztani a parcellák között, hogy mindegyik kezelési mód csak egyszer szerepeljen minden sorban és oszlopban. A 36 parcella között minden sorban, és ugyanígy minden oszlopban 720-720 különféle kombinációban tudjuk elrendezni a hatféle kezelési módot úgy, hogy megfeleljen a fenti feltételnek. Amennyiben a nagyszámú lehetséges elrendezés közül véletlenszerűen választunk egyet, akkor minden egyes parcella esetében azonos valószínűsége van annak, hogy azon egy bizonyos kezelési mód lesz alkalmazva. Ennek az a célja, hogy a kísérleti összehasonlításokból ki tudjuk zárni a teljes sorok vagy teljes oszlopok talajviszonyai közötti különbségek hatását.

Tételezzük fel, hogy egy kísérlet során a következő kezelési módok közötti különbségeket szeretnénk megvizsgálni:

Vagyis az egyes kezelési módok abban különböznek, hogy mennyi mesterséges talajjavító vegyszert juttatunk az egyes parcellák esetében a földbe.

A kísérlet végén a következő eredményeket kaptuk:

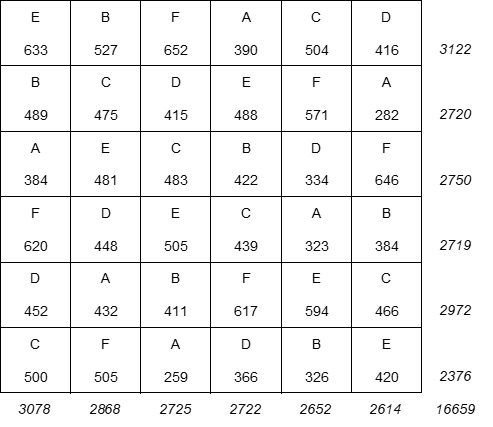
A latin-négyzet egyik nagy előnye, hogy felépítése miatt sokkal egyszerűbb az adatok feldolgozása és az ANOVA-táblázat elkészítése. A kéttényezős ANOVA-táblázat felépítését már több korábbi cikkben is ismertettem (Most nem almára lövünk - kéttényezős varianciaanalízis (Two-way - ANOVA), Hogyan csináld Minitab-bal – Kéttényezős varianciaanalízis (Two-way ANOVA)) és már ott is kiderült, hogy ez sajnos már nem olyan egyszerű, mint ahogy azt szeretnénk. Jelen esetben viszont kevesebb számítással is meg lehet oldani a feladatot.

Az üres ANOVA-táblázatunk így fog kinézni:

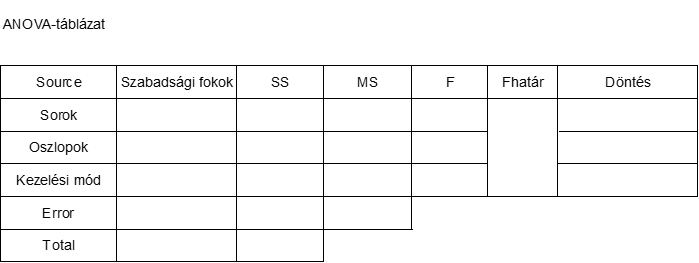
Kezdjük a szabadsági fokok számával. Mivel a hatféle kezelési mód a mátrix minden sorában és oszlopában is csak egyszer szerepel, ezért mind a sorok, mind az oszlopok szabadsági foka 6-1 = 5 lesz.

Mivel hatféle kezelési módunk van, ezért a kezelési módok szabadsági foka is ugyanannyi lesz.

Így az ANOVA-táblázat első három eleme be is kerülhet a táblázatba:

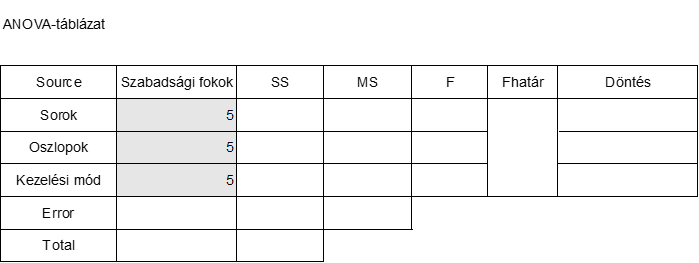
Mivel a kísérleti földterület 36 parcellát tartalmaz, ezért a teljes varianciára vonatkozó szabadsági fokok száma 6 x 6 – 1 = 36 – 1 = 35 lesz.

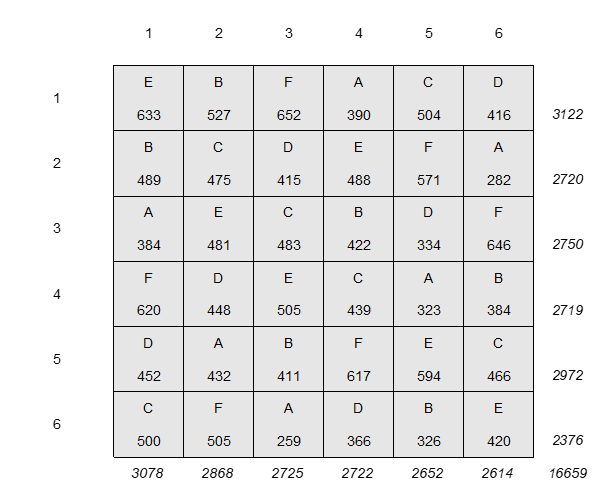
A teljes szabadsági fok is bekerülhet így az ANOVA-táblázatba:

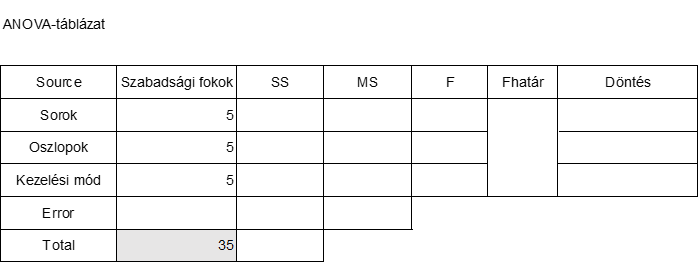
A hiba szabadsági foka úgy jön ki, hogy a Total szabadsági fokok számából kivonjuk az összes többit (35-5-5-5). Így a táblázatunk jelenleg a következőképpen néz ki:

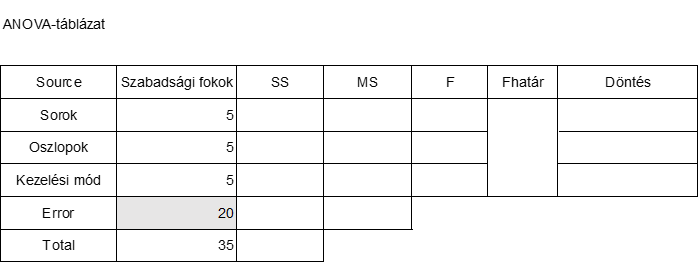
Akkor most töltsük ki a Sum of Squares (SS), azaz a négyzetösszegek oszlopok mezőit. A fenti táblázatban már összegeztük az egyes sorok és oszlopok terméshozamait. Most minden sor és oszlop terméshozamát elosztjuk a sorok és az oszlopok számával, azaz 6-tal. Így megkapjuk a sorokra és oszlopokra eső átlagos terméshozamokat. A teljes terméshozamot értelemszerűen elosztottam 36-al, így megkaptam az egy parcellára eső átlagos terméshozamot (462,750).

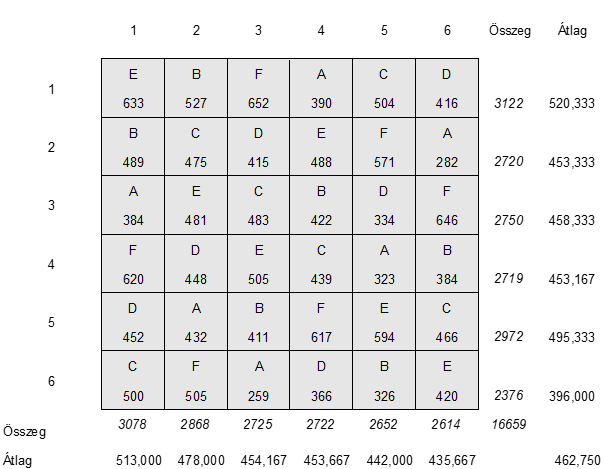
A következő lépésben arra vagyunk kíváncsiak, hogy vajon az egyes sorok, illetve oszlopok átlagai mennyire különböznek az összes 36 parcellára kiszámolt átlagos terméshozamtól. Ezért kiszámítjuk minden egyes sor és oszlop átlaghozamának különbségét a teljes terméshozam átlagától:

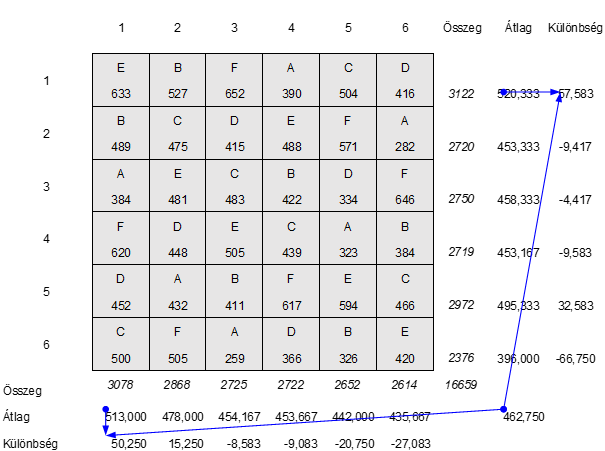
Például az első sor esetében az átlagos terméshozam 520,333, ez 57,583 egységgel több, mint a teljes földterületre eső átlag, amely 462,750 egység. Az első oszlop esetében ugyanígy az 513 egység 50,250 egységgel több, mint a teljes átlag 462,750 egység.

Mivel ez esetben is az egyes sorok és oszlopok NÉGYZETES eltérésére vagyunk kíváncsiak a vizsgálat során, ezért a különbségeket négyzetre emeljük:

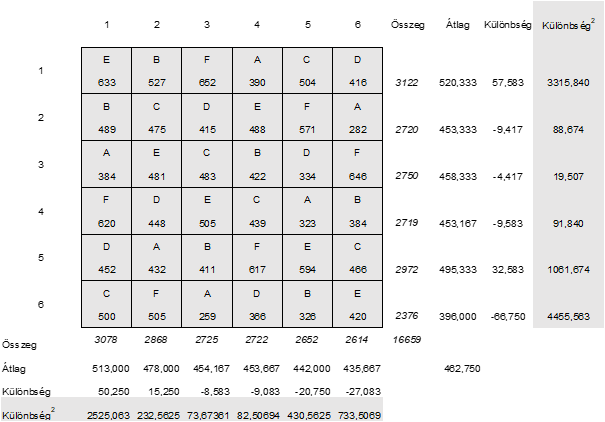
Az ANOVA táblázatban a sorokhoz és az oszlopokhoz tartozó SS-ként jelölt négyzetösszegeket úgy kapjuk meg, hogy összeadjuk az egyes sorokhoz és oszlopokhoz tartozó négyzetes különbségeket, majd ezeket megszorozzuk a sorok, illetve az oszlopok számával, jelen esetben 6-tal.

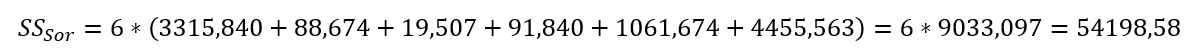
Az oszlopok esetében hasonlóképpen járunk el:

Ezzel a két adattal már ki is tudjuk egészíteni az ANOVA-táblázatunkat:

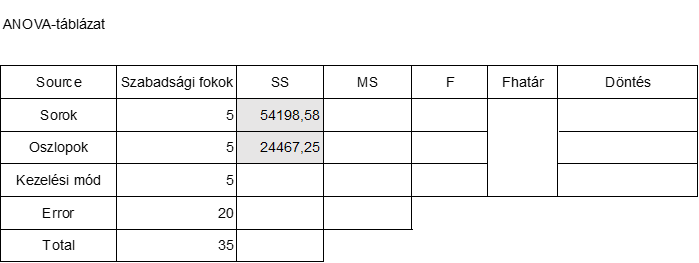
A következő lépésben nézzük meg, hogy az egyes kezelési módok esetében hogyan jön ki az SS négyzetösszeg. A dolog tulajdonképpen teljesen logikus, ha az egyes kezelési módok hatására vagyunk kíváncsiak, akkor a 36 parcella hozamait kezelési módonként kell csoportosítanunk. Például az A jelű kezelési móddal kezelt parcellák hozamait a következő módon kapjuk meg:

Így az A jelű parcellák terméshozamainak összege

A fentiekhez hasonló logikát követve össze tudunk állítani egy egyszerű táblázatot, amelynek segítségével megkapjuk a keresett négyzetösszeget:

A kezelési módokra vonatkozó SS négyzetösszeg így a következőképpen adódik:

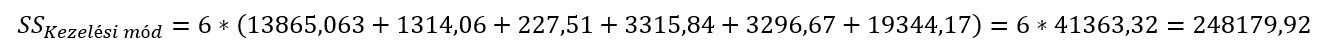
Az ANOVA-táblázatunk még egy értékkel gazdagabb lett:

A Total SS-t pedig úgy kapjuk meg, hogy kiszámítjuk mind a 36 parcella terméshozamának különbségét az átlagos terméshozamtól, majd ezeknek vesszük a négyzetösszegét. Ez lesz a leginkább sziszifuszi meló, mert mind a 36 parcella értékeit egyedileg kell kiszámolni.

Ebből is készítettem egy táblázatot, de ennek csak egy részletét másolom ide, mert kicsit hosszú lett:

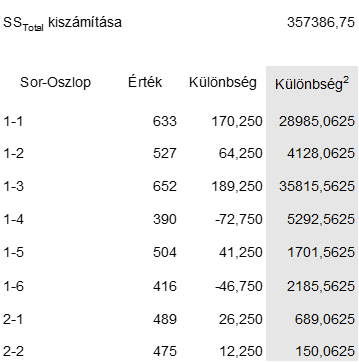
Így a teljes különbség négyzetösszeg 357386,75 lett. Ezt már szerencsére nem kell megszorozni 36-tal, úgyhogy ki is lehet tölteni a vonatkozó mezőt az ANOVA-táblázatban:

Az SS Error-t természetesen ismét úgy kapjuk meg, hogy az SS Totalból kivonjuk az összes többit:

Az MS oszlop, azaz a négyzetes átlagok oszlopát nem olyan nehéz kiszámolni, mert csak minden egyes sorban el kell osztani az SS-t a szabadsági fokok számával. Például a sorokra vonatkozó MS-értéket úgy kapjuk meg, hogy az SS értékét (54198,58) elosztjuk 5-tel, így megkapjuk az alábbi táblázatban látható 10839,716-ot. Mindhárom értéket kiszámolva az ANOVA-táblázat a következőképpen fog kinézni:

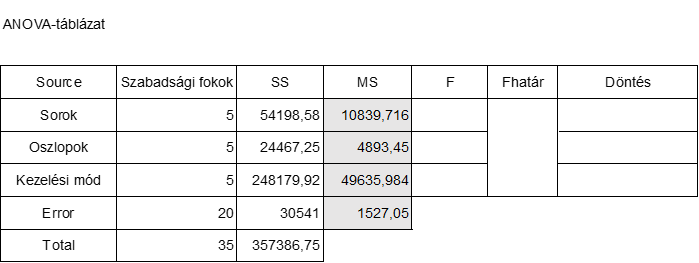
Ezek után a sorokra, az oszlopokra, illetve a kezelési módokra vonatkozó F-eloszlás értékeket úgy kapjuk meg, hogy a sorokhoz, az oszlopokhoz és a kezelési módokhoz tartozó MS-értékeket elosztjuk az Error-hoz tartozó MS-értékkel. Mivel tudjuk, hogy ha két egymástól független tényezőt vizsgálunk, amelyek nincsenek hatással egymásra, ezek varianciáinak hányadosa F-eloszlást (merthogy az F jelölés erre utal) követ, itt arra vagyunk kíváncsiak, hogy az egyes tényezők (sorok, oszlopok, kezelési módok) varianciája mennyire követi a véletlen törvényszerűségeit.

Az egyes tényezőkre vonatkozó F-értékek a következő módon adódnak:

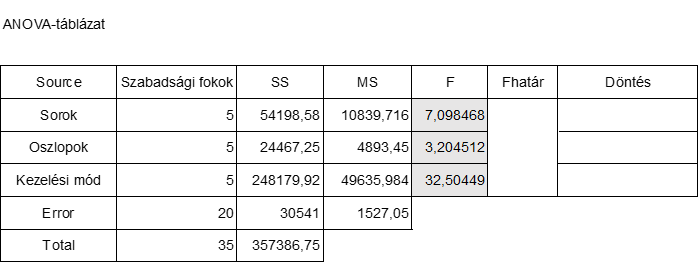
Az F-határértéket sajnos táblázatból kell kikeresnünk az adott tényezőre és az Error-ra vonatkozó szabadsági fokok ismeretében. Mivel minda a sorok, mind az oszlopok, mind pedig a kezelési módok szabadsági foka 5, az Error szabadsági foka pedig 20, ezért az F5,20-at kell kikeresnünk az F-eloszlás táblázatból:

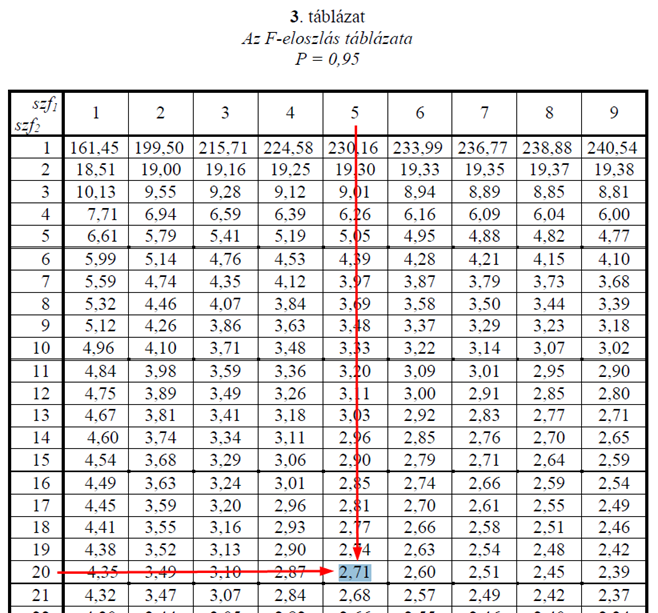
Így az ANOVA-táblázatunk utolsó előtti oszlopa is kitöltésre került:

Mivel mind a sorok, mind az oszlopok, mind pedig a kezelési módok esetében kapott F-értékek NAGYOBBAK, mint az F-határérték, ezért kijelenthetjük, hogy lényeges különbség lehet az egyes sorok és oszlopok termésátlaga, illetve a teljes földterület termésátlaga között. Minket azonban leginkább a kezelési módok hatása érdekel, ezért vegyük elő még egyszer a különféle kezelési módokra vonatkozó táblázatunkat:

Érdekes, hogy az A kezelési mód; vagyis, ha nem adunk egyáltalán sem nitrogént, sem pedig foszfátot a talajhoz, a terméshozam lényegesen alatta marad a teljes terület átlagos hozamának, hiszen az A kezelési mód átlagos hozama csak 345 egység, míg a teljes területé 462,75, azaz a hozam -117,75 egységgel kevesebb. A C esetben, ahol csak 1 egységnyi foszfát került a földbe, de nitrogén nem, az átlag majdnem megegyezik a teljes terület átlagával. A legnagyobb eltérést az F kezelési mód hozta, hiszen amikor 1 egység nitrogén és 2 egység foszfát került a talajba, akkor a terméshozam messze magasabb volt az átlagosnál.

És akkor körülbelül itt értem a végére a vizsgálatnak. Lehetne még boncolgatni, hogy a sorok és az oszlopok miért vannak szignifikáns hatással a termésátlagokra, ha a parcellák teljesen véletlenszerűen kerültek kiosztásra, de erre vonatkozóan nem találtam további tényfeltáró adatot.

Annak ellenére, hogy a latin négyzet valamivel egyszerűsítette a feldolgozást, a varianciaanalízis még mindig eléggé bonyolult és sok lépésből áll, de azért még mindig egy fokkal egyszerűbb, mint az általános eseté, amelyet a fentebb hivatkozott cikkekben boncolgattam. Persze, amint az látható, a feladat elvégezhető kézzel, vagy táblázatkezelő segítségével is, de a megfelelő statisztikai szoftverek alkalmazása ez esetben már jelentős megtakarítást jelent időben és a ráfordított munka tekintetében is. 

Mint látható, a randomizáció segítségével sikerült jónéhány bizonytalansági faktort kizárni a vizsgálatból – mint például a különféle időjárási tényezők, a talaj változékonysága, stb. – amelyek eddig zavarták az eredmények összehasonlíthatóságát.

Fischer csak 1935-ben publikálta hivatalosan a randomizáció módszerét a The Design of Experiments című könyvében, a feldolgozott adatsor is ebből a könyvből származik.

A könyv érdekessége még, hogy a módszer lényegét a híres Lady tasting tea példáján keresztül mutatja be, amely történet még megér majd egy misét…

Források:

Rothamsted Experimental Station 1919-1933, Rare books and manuscripts, The University of Adelaide
https://www.adelaide.edu.au/library/special/exhibitions/significant-life-fisher/rothamsted/

R. A. Fischer: Studies in Crop Variation, 1. An examination of the yield of dressed grain from Broadbalk, from the Journal of Agricultural Science, Vol XI. Part II, April 1921
https://www.adelaide.edu.au/library/special/exhibitions/significant-life-fisher/rothamsted/StudiesinCropVariation.pdf

Statistical Methods for Research Workers. 1st edition (Edinburgh: Oliver and Boyd, 1925)
http://www.haghish.com/resources/materials/Statistical_Methods_for_Research_Workers.pdf

R. A. Fischer: The Design of Experiments, Oliver and Boyd, Edinburgh – London, 1935
http://tankona.free.fr/fisher1935.pdf

R. A. Bailey: Latin squares: Some history, with an emphasis on their use in designed experiments
http://www-groups.mcs.st-andrews.ac.uk/~rab/histLSBMChand.pdf

Rothamsted Experimental Station report for 1932
http://www.era.rothamsted.ac.uk/eradoc/article/ResReport1932-3-230

Latin square design
http://www.stat.tamu.edu/~hart/652/anova4.pdf

Real Statistics using Excel – Latin Square design
https://www.real-statistics.com/design-of-experiments/latin-squares-design/