Egy héttel ezelőtt részletesen lépésről lépésre kiszámoltam Ronald Fischernek a Rothamsted Kísérleti Állomáson elvégzett latin négyzet kísérlettervének eredményei alapján, hogy az általa alkalmazott különféle műtrágyáknak van-e hatása a terméshozamokra (Káoszból rendet – Hogyan segít a véletlen rendet vágni a káoszban?). A példa arra mindenképpen jó volt, hogy a varianciaanalízis táblázat tartalmát részleteiben (ismét) megértsük (Most nem almára lövünk - kéttényezős varianciaanalízis (Two-way - ANOVA)). Ez viszont nem jelenti azt, hogy muszáj minden alkalommal ugyanezt a tortúrát végig játszani, arról nem is beszélve, hogy mennyivel nagyobb a hiba valószínűsége a kézzel történő számolgatás során. A XXI. században azonban már rendelkezésünkre állnak olyan eszközök és szoftverek, amelyek segítségével akár néhány mozdulattal megkaphatjuk ugyanezt az eredményt. Szerencsére most már az elemzés tartalma is érthetővé vált, így nem érdemes a kézzel történő számolással büntetnünk magunkat.

Eddig a Minitab programot használtam erre, ezt tulajdonképpen most is megtehetném. A Mintab használatáért viszont fizetni kell, így sokan inkább lemondanak róla. A Minitab helyett ma inkább az R statisztikai programnyelvre épülő RStudio programot választottam. Az R és az RStudio legnagyobb előnye az, hogy ingyen van. Emiatt igen elterjedt az alkalmazása, és moduláris felépítése miatt rengeteg különböző funkciója van. Ami szerintem hátránya (de ez szigorúan a személyes véleményem), hogy a kezelése nem igazán felhasználóbarát. Az még csak hagyján, hogy az R egy programnyelv, az RStudio pedig szigorúan véve egy programozási környezet, ezt még meg lehetne szokni. Ami számomra nehézkessé teszi az alkalmazását, az az igen változatos szintaxis, azaz programozási szabálykörnyezet. Az R és az RStudio közösségi alapon fejlődik, azaz sokan írnak hozzá sokféle alkalmazást, emiatt a különböző fejlesztők a saját személyes preferenciáik alapján építik fel az alkalmazás könyvtáraikat (library). Ez persze egy igen gazdag, színes és egyben kaotikus kavalkádot eredményez. Ennek a legnagyobb hátránya az, hogy az R és az RStudio alkalmazása sokkal több időt és erőfeszítést igényel a felhasználótól, vagyis azon felül, hogy meg kell tanulnia a különféle statisztikai eszközök alkalmazását, még félprofi programozóvá is kell válni, illetve el kell sajátítani a különféle alkalmazás könyvtárak egyedi programnyelvi elemeit és logikáját is.

Ez a másik oldalon persze sokkal nagyobb szabadságot is jelent, az R segítségével olyan dolgokat is meg lehet csinálni, amit sem a klasszikus táblázatkezelők, sem az egyéb statisztikai programcsomagok nem nyújtanak. Az ingyenesség mellett ez a másik szempont, amely miatt esetleg érdemes belefogni az R alkalmazásának elsajátításába.

Pont a fentiek miatt nem tudom felvállalni azt, hogy részletesen ismertetem az R programnyelv és az RStudio alkalmazását, most tényleg csak azt szeretném bemutatni, hogyan lehet kiértékelni az R segítségével a cikk témájaként megadott latin négyzet kísérletterv eredményeit.

Idézzük fel, hogyan is szólt a feladat:

Tegyük fel, hogy 6 különféle kezelési mód hatásait szeretnénk összehasonlítani. Ekkor egy adott földterületet (amely nem szükségszerűen négyzet alakú) osszunk fel 36 körülbelül egyforma parcellára. a hatféle kezelési módot (A, B, C, D, E és F) el tudjuk úgy osztani a parcellák között, hogy mindegyik kezelési mód csak egyszer szerepeljen minden sorban és oszlopban.

Tételezzük fel, hogy egy kísérlet során a következő kezelési módok közötti különbségeket szeretnénk megvizsgálni:

Vagyis az egyes kezelési módok abban különböznek, hogy mennyi mesterséges talajjavító vegyszert juttatunk az egyes parcellák esetében a földbe.

A kísérlet végén a következő eredményeket kaptuk:

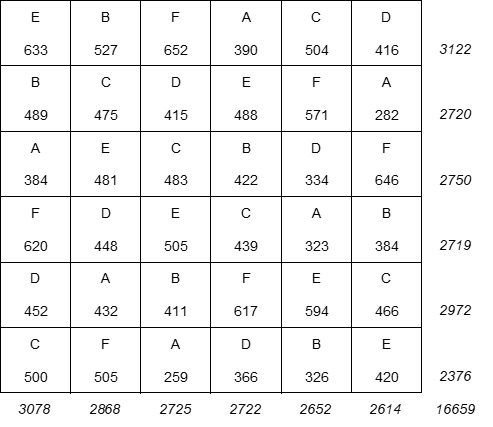
A mostani megoldásnak két célja van. Egyrészt szeretném ugyanazt az ANOVA-táblázatot létrehozni, mint amit a fent idézett cikkben kézzel számoltam végig, másrészt szeretném valamilyen módon vizuálisan is megjeleníteni az eredményeket. Akkor lássuk a feladat első felét:

Egy másik dolog, amit nem igazán kedvelek az R-ben, az az adatok kezelése. Félreértés ne essék, az R programnyelv igen gazdag a különféle adatfeldolgozási eszközökben és különösen a nagyméretű adatbázisok esetében sokkal előnyösebb az R adatmanipulációs eszközeinek az alkalmazása. Azonban akit a mai táblázatkezelő programok már elkényeztettek, annak nehéz rászokni arra, hogy begépelt parancsokkal, úgymond látatlanban rendezgesse az adattábláit. Szerencsére az RStudio képes adatfile-okat is beolvasni, ezért úgy döntöttem, hogy a kiinduló adattáblát táblázatkezelő programmal készítem el és aztán ezt fogom beolvasni az RStudio-ba. A fent egy 6x6-os táblában összegyűjtött adatokat átrendeztem egy adatbázishoz hasonló formába:

A táblázat első két oszlopa tartalmazza az egyes parcellák sor és oszlop azonosítóit a kiinduló táblázatnak megfelelően. A harmadik, Valtozat nevű oszlop tartalmazza, hogy az adott parcella milyen műtrágya kezelést kapott. A negyedik, Hozam, nevű oszlop pedig az egyes parcellák terméshozamát adja meg. Ezt a táblázatot gépeltem be, ügyelve arra, hogy ne hibázzak.

A kész táblázatot excel formátumban is be lehet olvasni az RStudio-ba, ehhez egy ’readr’ nevű alkalmazás könyvtárat kell telepíteni az RStudio-ba. Szerencsére ez nem bonyolult művelet, és ha mondjuk egy proxi nem tiltja le, akkor tulajdonképpen egy mozdulattal telepíthető az RStudio-ba. Én inkább azt preferálom, hogy a táblázatot elmentem pontosvesszővel elválasztott .csv file-ként, amelyet utána simán be tud olvasni az RStudio, nem kell hozzá telepíteni semmit. Azért preferálom a pontosvesszővel történő elválasztást, mert amikor a táblázatban van tizedestört, akkor onnantól komoly keveredések várhatók, mert bizonyos nyelveknél ponttal, más nyelveknél vessző a tizedesjel. Ha pontosvesszővel választjuk el az adatokat, akkor egy egyszerű szövegszerkesztővel egy ’keres/cserél’ parancssal egyszerűen ki tudjuk cserélni a tizedesjelet arra, ami nekünk megfelelő. Az R és az RStudio általában pontot használ tizedesjelként, míg mi magyarok általában vesszőt használunk erre a célra.

Első lépésként ki kell választani az ’Import Dataset’ parancsot az RStudio jobb felső ablakában, majd a legördülő menüből az ’From CSV’ parancsot.

Ekkor megjelenik egy ablak, ahol az adattáblázatot be lehet olvasni. Először ki kell jelölni a beolvasandó file-t.

A file megnyitási ablakban válasszuk ki a beolvasandó file-t.

A beolvasás nem igazán lett sikeres, mert az összes adatot egyetlen oszlopba olvasta be a program. Ennek persze az az oka, hogy a beolvasásnál az van beállítva, hogy elválasztóként (delimiter) vesszőt keressen az RStudio.

Ha itt ’comma’ helyett a ’semicolon’-t választjuk, akkor már helyesen fognak megjelenni az oszlopok.

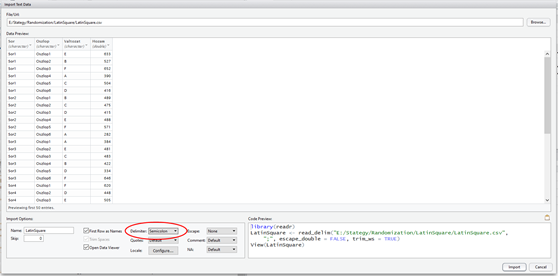
Az importálás után a jobb felső ablakban megjelenik a tábla a változók listájában, illetve a bal felső szekcióban is megjelenik egy ablak, amelyben a táblázat tartalma látható.

Most már megvan az adatsorunk, megkezdhetjük a feldolgozást. Először csak úgy a poén kedvéért készítsük el a változatok és a terméshozamok mátrixát. Ennek kevés jelentősége van a végeredmény szempontjából, inkább csak vizualizációs céllal készítettem el őket. Noha ezeket a parancsokat be lehet írni a bal alsó sarokban található terminál ablakba is, de én jobban kedvelem, ha létrehozok egy szkript file-t és a parancsokat ide írom be. Az egyes parancssorokat nemcsak együtt, hanem soronként is lehet futtatni a CTRL+Enter megnyomásával.

A két parancssort lefuttatva kaptam két mátrixot. A mátrixok nevei természetesen megjelentek a változók között.

A mátrix nevét egyszerűen beírva a terminál ablakban megjelennek a létrehozott mátrixok.

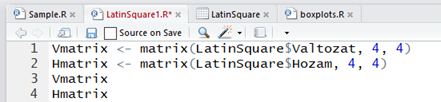
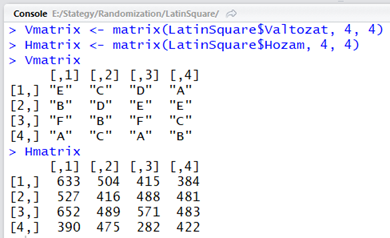
Amint azt fentebb említettem, első célunk az ANOVA-táblázat létrehozása. Ezt sajnos nem tudjuk egy lépésben elvégezni, először létre kell hoznunk egy úgynevezett linear model-t. A linear model egy olyan adathalmaz, amely rendezett formában tartalmazza a megadott adatkapcsolati modellnek megfelelő lineáris regressziós egyenes egyenletének alkotórészeit. A myfit változóban az lm() függvény alkalmazásával tudom létrehozni a lineáris modellt. Ehhez két dolgot kell megadnom a függvény hívásakor. Az egyik az adattábla, amelynek az adatait használnia kell a függvénynek. A másik pedig az egyes oszlopok közötti kapcsolatot kell definiálni. Jelen esetben a Hozam oszlop függ a soroktól, az oszlopoktól és a változattól, így az lm() függvény a következőképpen néz ki.

Ha latin négyzet alapján hoztuk létre a kísérlettervünket, akkor ezen a modellen nem igazán kell változtatnunk, de érdemes végig gondolni, hogyan szeretnénk feldolgozni az adatainkat. A myfit adatsort megjelenítve a következőket láthatjuk.

A 'Call:' után igazából csak azt láthatjuk, hogy milyen paraméterekkel hívtuk meg az lm() függvényt. Ez azért jó, hogy ha a függvényt többféle model alapján is lefuttatjuk, akkor a későbbiekben be tudjuk azonosítani az egyes változatokat. A 'Coefficients:' szekcióban pedig a regressziós egyenes paramétereit láthatjuk (Legyenek a négyzetek minél kisebbek…! – útban a lineáris regresszió elemzés felé., és Tudom, hogy gőzgép, de mi hajtja? – Egyváltozós lineáris regresszió – a regressziós egyenes meghatározása).

Erre a lépésre kizárólag azért volt szükség, hogy végül egyetlen egyszerű mozdulattal létrehozhassuk az ANOVA-táblánkat. Ezt a következő nem túl bonyolult parancs segítségével tehetjük meg.

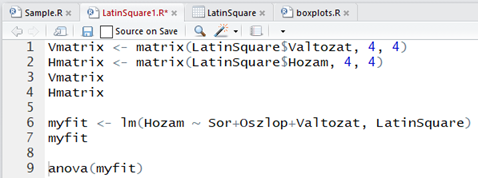
Az eredmény ilyen formában a jobb alsó terminál ablakban fog megjelenni.

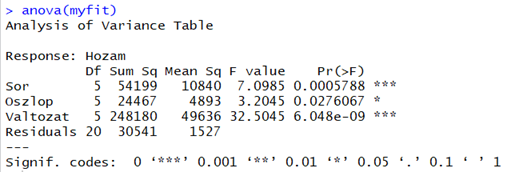
Szerencsére ugyanazokat a számokat kaptuk meg itt, mint amiket a korábbi kézzel elvégzett számítások során. Az egyetlen különbség a táblázat végén található, mert itt nem az F-értéket és az F-határértéket találjuk, hanem a P-value-t (A titokzatos P színre lép – Mi az a P-Value?). Ezek mögött pedig csillagokat látunk, amelyek azt jelölik, hogy milyen megbízhatósági szinten fogadhatjuk el az ellenhipotézist. A riport alján található kódmagyarázat alapján nagyjából úgy értelmezhető ez a kódrendszer, hogy ha csillagokat látunk, akkor az adott tényező a csillagok számának megfelelő megbízhatósági szinten fogadjuk el, hogy az adott tényező a megadott megbízhatósági szinten HATÁSSAL VAN a kimeneti érték változására. Amennyiben pont vagy üres mező lenne a P-érték mögött, akkor viszont elfogadjuk a nullhipotézist és azt, hogy az adott tényező NINCS HATÁSSAL az eredményre.

A mi esetünkben azt látjuk, hogy mind a sorok, mind az oszlopok, mind pedig a kezelés módja hatással van a terméshozamra. Ez pontosan ennyit jelen és nem többet, vagyis meg kell néznünk ezeket a hatásokat konkrétan. Úgy gondoltam, hogy ezúttal grafikusan fogom ábrázolni az egyes tényezők hatását boxplot diagramok segítségével. Az R-ben az egyik lehetőség erre a ggplot2 library alkalmazása. Ennek a csomagnak egy kicsit fura szintaxisa van, érdemes egy kicsit utánajárni csomag megalkotása mögötti logikának, mert csak a háttér megértésével lehet hatékonyan és gyorsan grafikonokat készíteni. Először is be kell tölteni az alkalmazás könyvtárat:

A grafikák adatainak beállítását a ggplot() függvény és ezen belül az aes() függvény meghívásával lehet beállítani. A ggplot függvény paraméterei a használt adattábla neve és a diagram alapbeállításai. Az aes() (aesthetics) függvényen belül a diagramok kinézetére vonatkozó beállításokat tudjuk elvégezni. Itt most csak az x és az y tengelyen ábrázolt értékeket állítom be. Ez így néz ki:

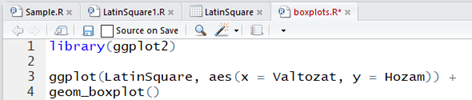
A geom_boxplot() függvény azt mondja a programnak, hogy rajzoljon az előre megadott paraméterek alapján egy boxplot diagramot.

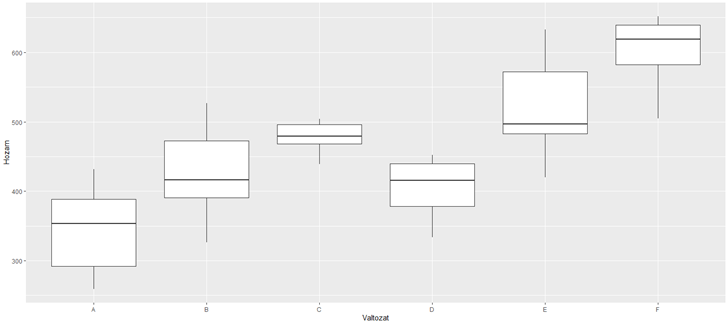
S lám, meg is kaptuk a bal alsó ablakban a kért boxplot-ot. Az x-tengelyen az egyes kezelési módok láthatók, az y-tengelyen pedig az egyes kezelési módokkal kezelt parcellák terméshozamait látjuk. És ahogyan vártuk, minél több foszfátot adunk a talajhoz, annál több lesz termés. De ha még nitrogént is adagolunk a foszfát mellé, ez tovább emeli majd a hozamot!

Most nézzük meg ugyanígy a sorok és az oszlopok hatását:

Az 5-ös és a 7-es sorokat lefuttatva a következő két diagramot kapjuk:

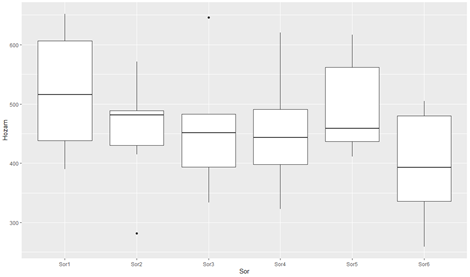
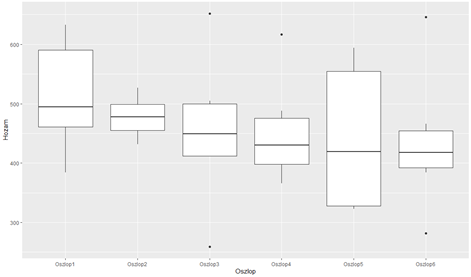
A soronkénti és oszloponkénti hozamok szintén változó tendenciát mutatnak, de erre nem találtam ésszerű magyarázatot. Valószínűleg a talajban vagy a vetőburgonya minőségében lehettek különbségek. Sajnos teljesen ezeket a változásokat sem lehet teljesen figyelmen kívül hagyni, bár ezek a tényezők valamivel kisebb hatást gyakoroltak a terméshozamra, mint a műtrágya használat.

Végül egy összefoglaló diagram, amely egészen használhatónak tűnik:

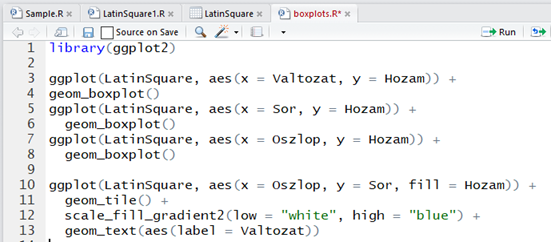
A 10-13 sorokban nem a geom_boxplot, hanem a geom_tile függvényt hívtam meg. A 10. sorban az x-tengelyen az oszlopokat, az y-tengyelen a sorokat ábrázoltam, így tulajdonképpen megkaptam a 36 parcella képét hasonlóan a cikk elején alkalmazott táblázathoz. A 11. sorban meghívtam a geom_tile() függvényt, ez egy mátrix-jellegű csempe-diagramot fog rajzolni. A 12. sorban megadtam a csempék színekkel történő kitöltéséhez az útmutatót. Itt színeket adhatok meg az alacsony (low), a közepes (middle) és a magas (high) értékekhez. Jelen esetben csak az alacsony és a magas értékekhez adtam meg színt, szerintem így néz ki a legjobban a diagram. A 13. sorban pedig megkértem a programot, hogy írja rá mindegyik csempére, hogy melyik kezelési módot alkalmazták az adott parcellán. A csempediagram pedig így néz ki:

Ez így egyfajta hőtérképet ad a területről és a 36 parcelláról. Minél magasabb a terméshozam, annál sötétebb szín jelenik meg az adott parcellán, vagyis az A, és a B parcellák világosabb, az E és az F parcellák sötétebb színűek. Fontos még, hogy ha össze akarod hasonlítani a cikk elején lévő grafikont ezzel a grafikonnal, akkor vedd észre, hogy a fenti ábra első sora ezen a diagramon legalul található. Az oszlopok sorrendje helyes.

Tudom, hogy a folyamat leírása messze nem olyan részletes, amely alapján megtanulhatnál R-ben programozni, de talán kedvet kapsz arra, hogy egy kicsit utána olvass, hogyan is működik ez a program.

Források:

R-bloggers: Latin square design in R
https://www.r-bloggers.com/2010/01/latin-squares-design-in-r/

Hadley Wickham: Elegant Graphics for Data Analysis, Springer