Szerencsém van. Ezt a blogot időnként az élet írja. Most is ez történt, egy kedves barátom hívott fel azzal, hogy egy ismerőse a segítségemet szeretné kérni egy garanciális reklamációval kapcsolatban, valamiféle statisztikai elemzés elkészítésével kapcsolatban lenne kérdése. Ennél többet ő sem tudott mondani, de nem kellett kétszer szólnia, egy-egy ilyen megkeresés jó lehetőséget jelent egy kicsit megtornáztatni az agysejteket. Végül a barátom ismerőse is felhívott és tömören elmagyarázta a helyzetet és a problémáját a statisztikai elemzéssel kapcsolatban.

És itt kissé meglepődtem, mert a kérdés nem volt szokványos. Gondoltam, majd küld egy adatsort, azt egy kicsit elemezgetem és majdcsak kilyukadunk valahol. De nem ez történt. Az ismerős elmesélte, hogy egy új termék gyártásának indításakor volt egy rövid időszak, amikor a gyártás egy szerencsétlen beállításnak köszönhetően egy darabig potenciálisan hibás termékeket gyártottak és értékesítettek a vevőjüknek. A probléma akkor eszkalálódott, amikor a vevő megreklamált egyetlenegy hibás terméket! Sajnos a hiba jellege miatt viszont felmerült, hogy kb. 10 000 darab terméket esetlegesen vissza kell hívni a piacról, ami azért mindkét félnek igen fájdalmas lenne. A vevő annyit kért, hogy az ismerős adjon egy becslést arra vonatkozóan, vajon még hány darab reklamáció várható emiatt a hiba miatt.

Ez egy kicsit más volt, mint amire számítottam. Igazából nem is tudtam volna válaszolni a kérdésre, ha nem pont most írtam volna meg azt a bizonyos cikket a RAND-ról és a potenciális atomfegyver baleset esélyének kiszámításáról (Robban vagy sem? – Megjósolható-e egy esemény valószínűsége, ha még sohasem történt meg ezelőtt?). Ez volt az egyetlen ok, ami miatt nem ért teljesen felkészületlenül a kérdés.

Először binomiális eloszlással (A binomiális eloszlás - lépjünk szintet az érmedobálásban) próbálkoztunk, mert a kérdést egy kicsit átfogalmazva tulajdonképpen ide jutunk. Ha 10 000 darab termék közül egy hibást találtunk, akkor mekkora a valószínűsége annak, hogy 1, 2, 3, 4, … darab hiba van a 10 000 darabos tételben? A binomiális tétel képlete a korábban tanultaknak megfelelően a következő:

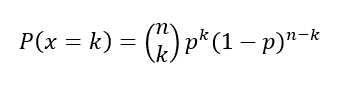
ahol

p – a hiba előfordulásának valószínűsége,
n – a minta összes eleme,
k – a mintában található hibás elemek száma.

A mi esetünkben

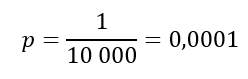
Ha arra vagyunk kíváncsiak, hogy mennyi annak a valószínűsége, hogy ez az egy termék hibás egyedül a 10 000 darabos tételben, akkor azt úgy kapjuk meg, hogy

Amennyiben a fentihez hasonlóan végig számoljuk, hogy mekkora lenne az esélye annak, hogy 2, 3, 4 … 10 termék esik ki, akkor a következőket kapjuk:

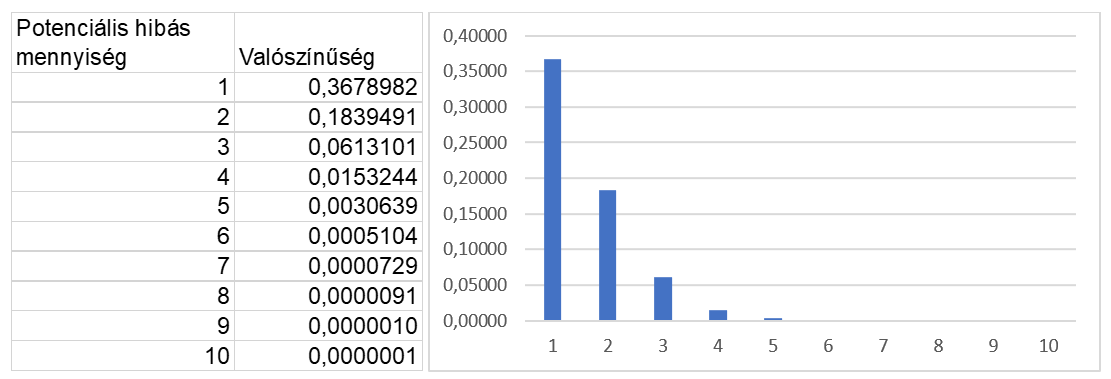
A táblázat adataiból jól látható, hogy ha a 10 000 darabból csak 1 darab volt hibás, akkor annak már csak 1,5% az esélye, hogy 4 hibás darab van a tételben, annak a valószínűsége pedig már csak 0,3%, hogy 5 a hibás darabok mennyisége.

Igen ám, de ez a 10 000 darabos tétel csak egyetlen mintának számít az általunk nem ismert sokaságból. Sajnos azt nem tudjuk, hogy ha a gyártás még tovább folytatódott volna a hibás beállításokkal, és kiveszünk ebből az elméleti sokaságból még sokszor 10 000 darabot, azokban vajon hány hibás darabot találnánk. Vagyis szükségünk lenne egy megbízhatósági intervallumra, amely megmondja, hogy a legrosszabb esetben hány hibás darabot találnánk a tételben.

Elvileg binomiális eloszlás esetén alkalmazni lehetne a normál eloszlást közelítésként, de csak akkor, ha ’n’ nem túl nagy és ’k’ nem túl kicsi. Sajnos ez esetben ez nem áll fent, hiszen n = 10 000 és p = 0,0001. Ilyenkor támaszkodhatunk arra a szabályra, hogy ha n nagyon nagy, p pedig nagyon kicsi, akkor a binomiális eloszlás jól közelíthető egy olyan Poisson-eloszlással (A kis számok törvénye, avagy halálos lórúgások a porosz hadseregben - A Poisson-eloszlás) ahol a Poisson-eloszlás Lambda tényezője λ = n * p.

Hogyan is néz ki ez esetben a kis példánk.

Mivel n = 10 000 és p = 0,0001, ezért nem meglepő, ha ez esetben λ = 1! Így amennyiben arra vagyok kíváncsi, hogy egy ilyen ritka előfordulás esetében mekkora annak a valószínűsége annak, hogy ez az egyetlen darab fog kiesni, úgy a következőt kapom:

Mivel λ = 1, ezért e (az Euler-féle szám) a -1-dik hatványon, az egyenlő 1/e-vel, illetve Lambda az első hatványon egyenlő Lambdával, az 1! pedig egyenlő 1-gyel, ezért a keresett valószínűség 0,36787 lesz. Visszapillantva a fenti táblázatra, észrevehetjük, hogy ez az érték majdnem megegyezik a binomiális eloszlás alapján kapott eredménnyel. Ugyanezt a képletet alkalmazva végig számoltam a binomiális eloszlás alapján ugyanazokat a valószínűségeket és a következő táblázatot kaptam:

A binomiális-, és a Poisson-eloszlás alapján kapott valószínűségek között csak a negyedik – ötödik tizedesjegy környékén vannak eltérések, vagyis a feltevésünk beigazolódott. És most lássuk a megbízhatósági intervallumok kiszámításának módját. Ez egy érdekes dolog, mert a matematika története során összesen 19 különféle módszert dolgoztak ki a Poisson-eloszlás megbízhatósági határainak kiszámítására! Szerencsére egy olyan módszer van, ami eléggé elterjedt és ráadásul nem is túl bonyolult. Ez a módszer azt a törvényszerűséget használja ki, hogy a Poisson-eloszlás kummulatív értékei arányosak egy 2x paraméterű Khí-négyzet eloszlás értékeivel. Ezt matematikásan egy eléggé csúnya képlettel lehet leírni.

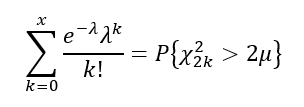
Vagyis amennyiben arra vagyunk kíváncsiak, hogy mekkora annak az esélye, hogy maximum 3 hibás darabunk lesz, akkor a 0, 1, 2 és a 3 hibás darab Poisson-valószínűségeinek összege megegyezik egy ν = 6 paraméterű Khí-négyzet eloszlás értékével. A Khí-négyzet eloszlás segítségével viszont már akár egy táblázatkezelő program segítségével is ki tudjuk számítani az α/2= 0,025 és az (1- α/2) = 0,975 megbízhatósági szintekhez tartozó lehetséges kieső mennyiségeket. Ezeket az értékeket egyébként táblázatos formában is megtalálhatod a www.statisticshowto.com oldalon a források között található linken. Eredményként a következő táblázatot kaptam:

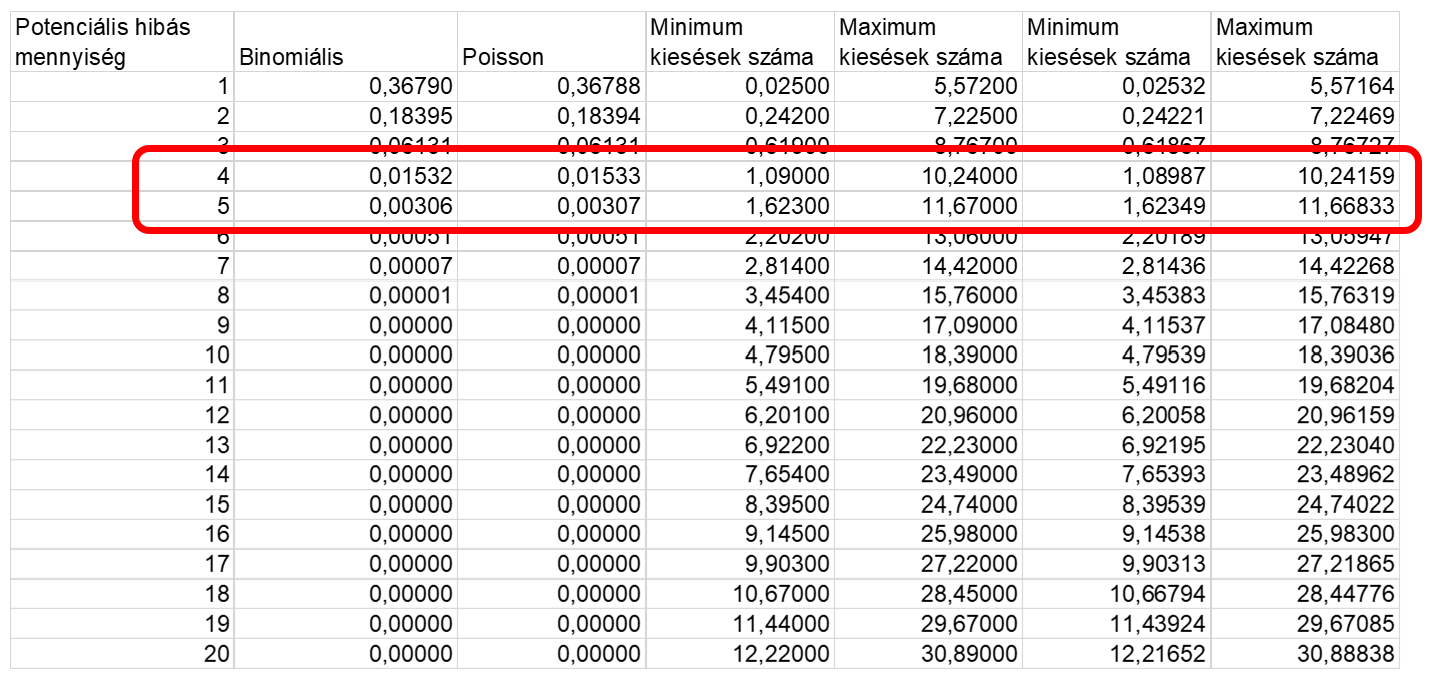
Vagyis így a becslés eredménye az, hogy 95%-os valószínűséggel maximum 10 hibás darab, 99%-os valószínűséggel pedig 12 darab fog még kiesni.

Források:

V.V. Patil, H.V. Kulkarni, REVSTAT – Statistical Journal, Volume 10, Number 2, June 2012, 211–227
https://www.ine.pt/revstat/pdf/rs120203.pdf

Anwer Khurshid: Confidence Intervals for the Mean of a Poisson Distribution: A Review, January 1993, Biometrical Journal 35(7):857 - 867
https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.900.3700&rep=rep1&type=pdf

Statistics Howto - What is a Binomial Confidence Interval?
https://www.statisticshowto.com/binomial-confidence-interval/