Az egyik előző bejegyzésben meséltem el a USS Scorpion megtalálásának történetét (A USS Scorpion nyomában – A Bayes-i keresési algoritmusokról). A történet annyira fellelkesített, hogy úgy döntöttem, valahogyan kipróbálom, hogyan is működik ez a gyakorlatban.

Szerencsém volt, találtam egy cikket, amely részletesen leírja, hogyan lehet egy ilyen keresést elkészíteni. A cikk nem konkrétan a USS Scorpion keresését használja fel példaként, egészen egyszerűen csak készít egy kvázi adathalmazt, ami egyébként nem is megy az érthetőség rovására, így az egész számítási folyamat jobban követhetővé válik.

Az eszköz, amit alkalmazni fogok, viszont nem a tőlem megszokott táblázatkezelő, vagy a Minitab (amely egyébként nem is igazán alkalmas erre a feladatra), hanem az R. Valószínűleg táblázatkezelőben is el lehetne végezni az egész szimulációt, de – szerintem legalábbis – sokkal bonyolultabban lehetne elvégezni, mint az R programmal. Vállalkozó szellemű olvasók táblázatkezelő programmal és végigszámolhatják ugyanezt a példát, csak hogy megtudjuk, mennyire problémás.

Az alapprobléma tehát az, hogy adott egy eltűnt objektum, amelyet meg kell keresnünk egy adott területen. Ezt modellezzük azzal, hogy létrehozunk egy olyan 61x61 cellából álló mátrixot, amely azt a területet reprezentálja, amely a keresésünk színhelye. Az egyes cellák mérete most nem érdekes, egyszerűen azt feltételezzük, hogy a keresett objektum a 61x61-es mátrix valamelyik cellájában van. R-ben ezt most nem egy mátrix-szal, hanem egy olyan adattáblával fogjuk jelölni, amelynek van egy ’x’ és egy ’y’ koordinátája. Most hozzuk létre ezt a táblázatot:

Ez az egy sor is már egy csomó magyarázatot igényel. A ’d’ betű lesz a neve az adattáblánknak. A <- jel R-ben az értékadást jelző operátor, vagyis most egy valamilyen értéket ad egy változónak, jelen esetben d-nek. A data.frame() függvény egy adattáblát hoz létre a zárójelben megadott paraméterekkel. A zárójelben a d tábla x és y oszlopainak adunk értéket. A rep() függvény valamilyen számsort hoz létre a zárójelben megadott szabályok szerint. A seq() függvény pedig egy szekvenciát generál szintén a zárójelben megadott szabályok szerint. Ez esetben az  x = rep(seq(-30, 30), each = 61) kifejezés azt jelenti, hogy a sorozat minden egyes értékét ismételje meg 61-szer. Az  y = rep(seq(-30, 30), times = 61) kifejezés pedig azt jelenti, hogy a létrehozott szekvenciát ismételje meg a rep() függvény 61 alkalommal. Ez a két paraméter általánosságban is igen hasznos lehet egy csomó esetben, amikor valamilyen mintázat szerint kell adatsorokat generálnunk. Így a következő táblázatot kaptuk:

Tehát van egy olyan adattáblánk, amelynek 3721 (61x61) sora és két oszlopa (változója) van. Ez most így néz ki:

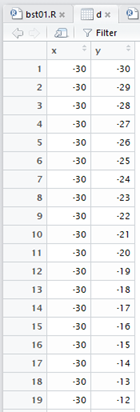
Ismerjük fel, hogy egy mátrix mezőit generáltuk, de ezek formátuma nem egy mátrix. Ennek az az oka, hogy a továbbiakban a mátrix minden egyes mezőjéhez több különféle értéket is hozzá fogunk rendelni, amit egy mátrix formátumú táblázat esetében nem tudnánk megtenni.

Most minden egyes cellához hozzá tudunk rendelni egy 0 és 1 közötti számot, amely azt a valószínűséget jelenti, hogy a keresett objektum abban a bizonyos cellában van. Kiinduló állapotként van egy sejtésünk arról, hogy a keresett objektum egy bizonyos cellában vagy annak környezetében van. Ezt úgy vesszük figyelembe, hogy minél közelebb van egy cella ahhoz a bizonyos cellához, annál nagyobb, minél messzebb van egy cella a kiindulóponthoz képest, annál kisebb a valószínűsége annak, hogy az objektum az adott cellában van. Ha azt feltételezzük, hogy ez a lokális valószínűség véletlenszerűen változik, akkor ezt modellezhetjük egy normál eloszlással is. Mivel a mátrixunk kétdimenziós, ezért ezt a valószínűséget egy kétváltozós normál eloszlással tudjuk a legjobban modellezni, amely azt jelenti, hogy egy adott x-y koordinátájú cella esetében a lokális valószínűséget az x-, és az y-irányú valószínűségek szorzata adja.

A LEP a Local Effectiveness Probability kifejezés rövidítése, amely azt adja meg, hogy mekkora az esélye annak, hogy a keresett objektum egy adott mezőben van. Vedd észre, hogy a fent generált táblázat egyes oszlopaira úgy tudunk hivatkozni, hogy az adattábla neve és az oszlop neve közé egy $ jelet teszünk. Ez igazából nem újdonság, táblázatkezelőben is hasonlóképpen tudunk hivatkozni egy adott munkalap adott cellájára, a logika ugyanaz. A másik trükk, ami a fenti kódsorban megfigyelhető, hogy nincs LEP nevű oszlop a táblázatban, akkor hogyan hivatkozhatunk rá? Nos, mivel ez esetben a <- operatáror azt mutatja, hogy ez egy értékadási művelet, így az R létre fog hozni egy új oszlopot a d adattáblában és az oszlop egyes mezőit soronként fel fogja tölteni a <- operátor után megadott kifejezés alapján. Érdekes, hogy ezt az oszlopot nem kell előre definiálni, úgymond „röptében” is létre tudjuk hozni. Ez a szabadság sokszor egyszerűsíti az életünket, viszont így nagyobb a hibázás esélye is.

A <- utáni kifejezés szintén érdekes. A kifejezés tulajdonképpen két függvény szorzata. Mindkét függvény a dnorm() függvényt használja. A függvény megadja egy adott x-értékhez tartozó adott átlagú és szórású normál eloszlás sűrűségfüggvényének értékét (Esemény valószínűségének kiszámítása normál eloszlású sokaság esetén). A dnorm() függvénynek három paraméterét kell megadni. Először azt az x értéket kell megadni, amelyhez tartozó sűrűségfüggvény értékre kíváncsiak vagyunk. A másik két paraméter a normál eloszlás átlaga és szórása, amelynek a sűrűségfüggvény értékére kíváncsiak vagyunk.

Ezek alapján a fenti kódsor először is létrehoz egy új oszlopot LEP néven, majd soronként feltölti az adott sorban lévő x és y értékekhez tartozó normál eloszlás sűrűségfüggvények x-hez és y-hoz tartozó értékeinek szorzatával. Az eredményt valahogy így lehet elképzelni:

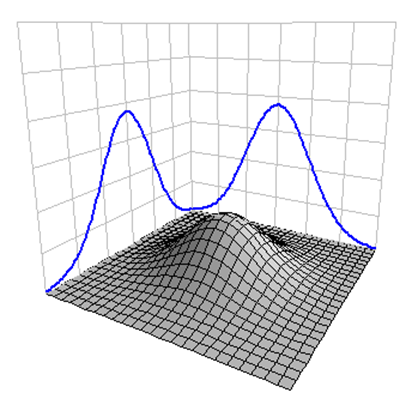
Az általam választott példa egy kicsit más ábrázolási módot választott az adatok megjelenítésére.

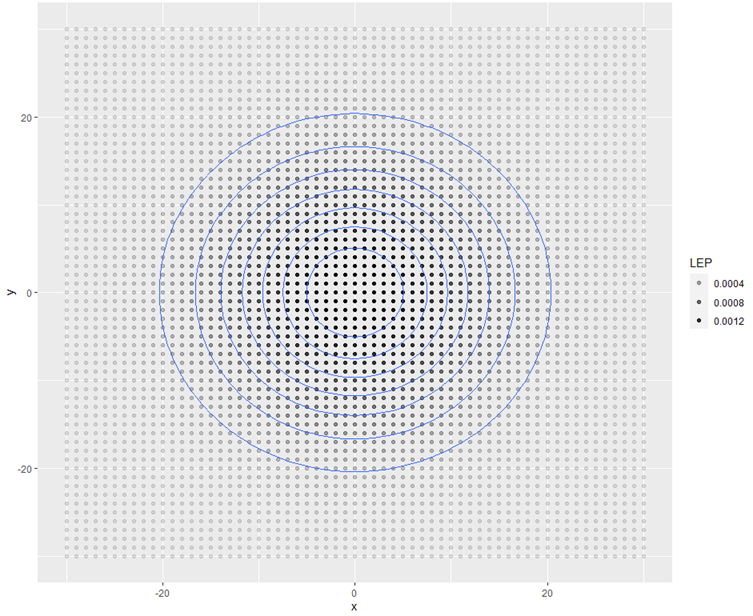
Ezt a grafikont úgy képzeld el, mintha az előző háromdimenziós ábrára felülről néznél rá, a kék körök pedig magassági vonalak lennének. A háttérben látható pontok az előzőleg definiált mátrix egyes mezőit reprezentálják. Minél sötétebb a pont színe, annál magasabb a valószínűsége, hogy a keresett objektum a mezőben található. A diagramot a szerző a ggplot2 csomag alkalmazásával készítette. Az R alap grafikája segítségével csak egyszerűbb, kevésbé látványos diagramokat lehet készíteni. A ggplot2 csomag segítségével sokkal látványosabb diagramok készíthetők, de a kód logikája jelentősen eltér a standard R script alapú nyelvétől. A diagramok úgy pakolhatók össze, mint egy lego darabkái. Nem nehéz, csak egyszer meg kell érteni a logikáját.  Ebben nagy segítséget nyújthat Hadley Wickham könyve, amely internetes könyv formájában ingyenesen elérhető a források között található linken.

A fenti diagramot a következő kódsor hozta létre:

A kódsor négy függvényt tartalmaz.

• ggplot() – Ez a ggplot2 csomag alapfüggvénye, gyakorlatilag ez a függvény rajzolja meg a diagramot a zárójelben lévő paraméterek alapján
• aes() – Ezzel a függvénnyel tudjuk befolyásolni a diagram megjelenését. Ezen belül lehet megadni a diagram x, y és z paramétereit, és az általános megjelenési tulajdonságokat, mint például a diagram stílusát, színét, a diagram címét és még sok minden mást. Ez a függvény nagyon gazdagon paraméterezhető, érdemes az egyes paraméterek használatának utánanézni. Amikor közvetlenül a ggplot() függvényben használjuk, akkor a diagramterület fő tulajdonságait tudjuk vele meghatározni. 
• geom_point() – Ezzel egy pontdiagramot tudunk létrehozni a diagramhoz kapcsolt adattábla alapján.
• stat_contour() – Ezzel a függvénnyel rajzoljuk ki a kék színű „magasságvonalakat”.

A kódsor felépítése is érdekes. A ggplot() függvény létrehozza a diagramterületet, ezután egy + jel segítségével hozzáadjuk a pont diagramot, amely a szürke pontokat adja hozzá az ábrához, a végén pedig egy másik + jellel és a stat_contour() függvénnyel a „magasságvonalakat” is hozzáadtuk. Ez a fajta modularitás a ggplot2 csomag előnye, mert a különféle adatokról szóló különféle diagramtípusokat tág határokon belül lehet kombinálni.

Mit is jelent akkor a fenti kódsor? Menjünk lépésről-lépésre:

Amint az megfigyelhető, a ggplot() függvény első paramétere a d adatttábla, ennek az adatait fogjuk használni a diagram megrajzolásához. Ezután jön egy aes() függvény, amelyen belül megadásra került x, y és z értéke. Mivel előzőleg már megadtuk, hogy a ’d’ táblázatot használjuk, ezért elég az oszlop vagy mező nevét megadni. Értelemszerűen x és y lesz a diagram x és y tengelyének koordinátái, a z tengelyen az adott pont magasságát pedig a LEP oszlop értékei adják majd meg. Ha ezt kirajzoltatjuk, akkor csak egy szürke négyzetet kapunk két koordináta tengellyel, amelyek az adatoknak megfelelően be is vannak osztva.

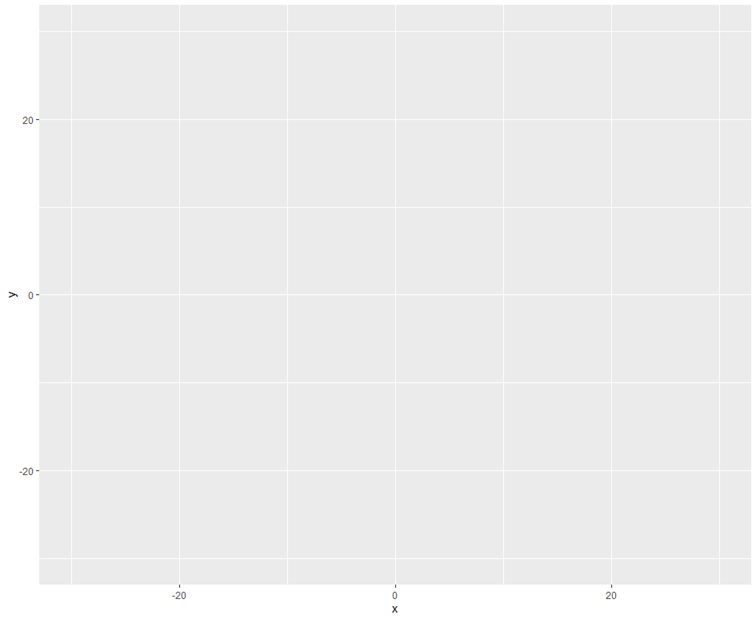
Ehhez most hozzáadjuk a pont diagramot:

A geom_point() függvényen belül szintén megadásra került egy paraméter az aes() függvényen belül. Az alpha = LEP annyit jelent, hogy a pontok színének árnyalatát a LEP oszlop értékei határozzák majd meg. Mivel kétdimenziós diagramot rajzolunk, ez egy praktikus módja az egyes mezőkhöz tartozó valószínűségek vizuális megjelenéséhez.

Végezetül hozzáadjuk a diagramhoz a „magasságvonalakat”:

Idáig készen is vagyunk, de még messze nem végeztünk. A jövő héten be fogom mutatni, hogyan vesszük figyelembe a szonár vagy más detektáló eszköz detektálási képességeit és ezek alapján hogyan határozzuk meg annak a valószínűségét, hogy egy adott mezőben megtaláljuk a keresett objektumot.

(Folytatása következik…)

Források:

R-Bloggers – Bayesian Search Models
https://www.r-bloggers.com/2014/03/bayesian-search-models/

Hadley Wickham: Elegant Graphics for Data Analysis, Springer, 2016
https://ggplot2-book.org/index.html

R ggplot2 cheat sheet
https://rstudio.com/wp-content/uploads/2015/03/ggplot2-cheatsheet.pdf