Ma ismét egy már korábban bemutatott témát próbálok újra feszegetni. Az elmúlt hetekben az egymintás Z-próba rejtelmeiben merültem el (Senki többet harmadszor? – Újra az egymintás Z-próbáról, most R-kóddal) és azt is megértettem, hogy mit is jelent az, amikor azt feltételezzük, hogy a teszt feltétele az adatok normál eloszlása (És mégis miért kellene normálisnak lennie?). Viszont azt is megtudtuk, hogy ez a próba csak akkor működik megbízhatóan, ha elegendően nagyszámú mintát veszünk ki a sokaságból.
De mihez kezdjünk azokkal az esetekkel, amikor valamilyen ok miatt nem áll elegendő minta a rendelkezésünkre? Ekkor kerül képbe az egymintás t-próba, amelyről már szintén esett szó (A sörfőző, aki forradalmasította a statisztikát). Az egymintás Z-próbával szemben ennek a tesztnek az az előnye, hogy kevesebb minta esetében is alkalmazható, illetve rafinált módon akkor is használható, amikor nem ismerjük a sokaság szórását, ilyen esetekben a minta szórásával helyettesítjük azt. Cserébe viszont a normál eloszlás ez esetben nem alkalmazható, hanem az úgynevezett Student-féle t-eloszlást vagyunk kénytelenek alkalmazni, amelyről azt tudjuk, hogy nem egyetlen függvény, hanem függvények sorozata. Attól függ, hogy melyik függvényt alkalmazzuk a megbízhatósági határérték kiszámítására, hogy mekkora a vizsgált mintánk elemszáma. A fenti diagramokon folytonos vonallal rajzoltam a t-eloszlás függvényeket, szaggatott vonallal pedig a hozzá tartozó normál eloszlás sűrűségfüggvény görbét. A diagramok felett látható ’szf’ a szabadsági fokok számát jelöli, amely egyszerűen eggyel kevesebb, mint a minta elemszáma (a szabadsági fokok számáról még tartozom egy cikkel, ezt igyekszem majd mielőbb pótolni).
A fenti diagramokon egészen jól látszik, hogy a kis minta elemszámok esetében jelentős eltérés van a t-eloszlás és a normál eloszlás görbe között. A szabadsági fokok számának (azaz a vizsgált minta elemszámának) növekedésével hogyan közelít a t-eloszlás görbéje a normál eloszlás görbéjéhez.
A fenti diagram teljes kódja így néz ki:
#A szükséges csomagok betöltése
library(ggplot2)
library(grid)
library(gridExtra)
#Diagramrajzoló függvény
tDistDiagram <- function(df)
{
szText <- as.character(df)
diagramTitle <- paste("szf = ", szText)
ggplot() + xlim(-4, 4) +
geom_function(fun = "dt", args = list(df = df), color = "darkgreen") +
geom_function(fun = "dnorm", args = list(mean = 0, sd = 1),
color = "darkgrey",
linetype = "dashed") +
labs(title = diagramTitle)
}
#A diagramok kirajzolása különféle szabadsági fokok függvényében
plot1 <- tDistDiagram(df = 1)
plot2 <- tDistDiagram(df = 2)
plot3 <- tDistDiagram(df = 3)
plot4 <- tDistDiagram(df = 4)
plot5 <- tDistDiagram(df = 5)
plot10 <- tDistDiagram(df = 10)
plot15 <- tDistDiagram(df = 15)
plot20 <- tDistDiagram(df = 20)
#A diagramok elhelyezése egymás mellett és alatt, + cím
grid.arrange(top = textGrob("t-eloszlás függvények különféle szabadsági fokokkal",
gp=gpar(fontsize=20,font=1)), plot1, plot2, plot3, plot4,
plot5, plot10, plot15, plot20, nrow = 2, ncol = 4)
A szükséges csomagok betöltésével nem töltenék sok időt. A ’ggplot2’ csomag a diagramok megrajzolásához szükséges függvényeket tartalmazza, a ’grid’ és a ’gridextra’ csomagok pedig a kód utolsó részében a diagramok táblázatos elhelyezéséhez, illetve a főcím kiíratásához szükségesek.
A kód második része egy függvény, aminek a diagramok megrajzolása a feladata. Mivel ez egy többször ismétlődő feladat, ezért érdemes egy paraméteres függvényt írni rá. A függvény egyetlen paramétere a szabadsági fokok száma (df). A függvény első két sora (a kapcsos zárójel után) csak amiatt kell, hogy a diagramok címét ki tudjam íratni. Az átadott df változót, amely egy szám, karakterekké kellett alakítani, illetve ez alapján meg kellett alkotni a diagram címét tartalmazó karaktert. Ezt egy szekvenciálisan megírt program esetében ezt minden szakaszban kézzel módosítani lehetne, de egy függvény esetében ezt a stringet mindig el kell készíteni a megadott paraméter alapján.
Ezután a ’ggplot()’ függvény segítségével kirajzoljuk a diagramterületet, illetve az ’xlim()’ függvény segítségével beállítjuk az x-tengely beosztását. Ezután a sor végi ’+’ jel segítségével hozzáadjuk a diagramterülethez a t-eloszlás és a normál eloszlás sűrűségfüggvény görbéket. A ’color’ és a ’linetype’ paraméterek segítségével megváltoztattam a függvények vonalának a színét és a vonalak típusát. Végül hozzáadtam a diagramhoz a korábban létrehozott címet.
A harmadik nagy szakaszban az előbb létrehozott függvény segítségével elkészítettem a 8 diagramot és mindegyiket elmentettem egy plot.. nevű változóban.
A negyedik rész tulajdonképpen egyetlen kódsorból áll, noha 3 sorba lett leírva. Ez a kódsor tulajdonképpen megszerkeszti a 8 diagramból álló táblázatot, illetve elhelyezi a főcímet a diagramok felett. A ’textGrob()’ függvény a diagram címét, mint grafikus elemet helyezi el a diagramok felett, a ’gpar()’ függvény pedig ennek a grafikus elemkét elhelyezett szövegnek állítja be a tulajdonságait, például a használt karakter típusát és méretét. Ezek után következnek a plot1, plot2, … diagramok, majd az ’nrow’ és az ’ncol’ paraméterekkel beállítottam, hogy a diagramok hány sorban és hány oszlopban helyezkedjenek el.
Visszatérve az egymintás t-próba témakörére, a következő kérdés az, hogy mi a különbség az egymintás Z-próba és az egymintás t-próba eredménye között. A korábbi cikkek alapján már sejthető, hogy az egymintás t-próba eredménye egy szimmetrikus, de szélesebb intervallum lesz, ahol az elemek 95%-a elhelyezkedik.
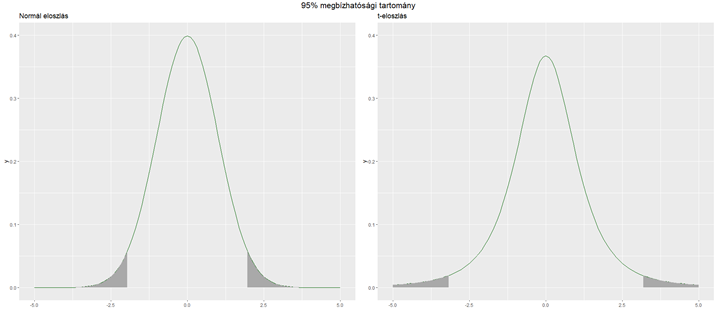
A fenti két diagram összehasonlítja a kétféle eloszlást hasonló paraméterekkel. A t-eloszlás középen egy kicsivel alacsonyabb, a két szélén viszont valamivel vastagabb. Így viszont a t-eloszlás esetében a 95%-os megbízhatósági tartomány szélesebb lesz. Ez esetben a normál eloszláshoz tartozó kritikus Z-érték 1,959, míg a t-eloszlás esetében a kritikus t-érték 3,18. Ezt a különbséget az alacsonyabb minta elemszám okozza, erre már utaltam korábbi bejegyzésekben (A nagy dobókocka kísérlet). Ezt a diagramot a következő kód segítségével készítettem el:
#A szükséges csomagok betöltése
library(ggplot2)
library(grid)
library(gridExtra)
#97,5%-os megbízhatósági határok kiszámítása
ciT95.1 <- qt(p = 0.975, df = 3)
ciN95 <- qnorm(p = 0.975, mean = 0, sd = 1)
#A jobboldali normál eloszlás diagram elkészítése
plot1 <- ggplot() + xlim(-5, 5) + ylim(0, 0.4) +
stat_function(fun = "dnorm",
geom = "line",
args = list(mean = 0, sd = 1),
color = "darkgreen") +
stat_function(fun = "dnorm",
geom = "area",
args = list(mean = 0, sd = 1),
fill = "darkgrey",
xlim = c(-5, -ciN95)) +
stat_function(fun = "dnorm",
geom = "area",
args = list(mean = 0, sd = 1),
fill = "darkgrey",
xlim = c(ciN95, 5)) +
labs(title = "Normál eloszlás")
#A baloldali t-eloszlás diagram elkészítése
plot2 <- ggplot() + xlim(-5, 5) + ylim(0, 0.4) +
stat_function(fun = "dt",
geom = "line",
args = list(df = 3),
color = "darkgreen") +
stat_function(fun = "dt",
geom = "area",
args = list(df = 3),
fill = "darkgrey",
xlim = c(-5, -ciT95.1)) +
stat_function(fun = "dt",
geom = "area",
args = list(df = 3),
fill = "darkgrey",
xlim = c(ciT95.1, 5)) +
labs(title = "t-eloszlás")
#A diagramok elhelyezése egymás mellett és a főcím kirajzolása
grid.arrange(top = textGrob("95% megbízhatósági tartomány",
gp=gpar(fontsize=16,font=1)),
plot1, plot2, ncol = 2)
A kód felépítése igen hasonló az előzőhöz, úgyhogy inkább a különbségeket szeretném kiemelni. Az első rész szinte ugyanaz, úgyhogy erre most nem vesztegetnék több szót. A második részben kiszámoltam a kétféle eloszláshoz tartozó 95%-os megbízhatósági határt. Az ehhez használt függvények a ’qt()’ és a ’qnorm()’ függvények használatával az adott eloszlás inverz értékét kapjuk meg. Ez annyit jelent, hogy ha megvan a sűrűségfüggvény görbe alatti területének az értéke, akkor a függvények alkalmazásával megkapjuk az ezekhez tartozó x-értékeket. Paraméterként azért 0,975-öt adtam meg, mert kétoldali tesztről van szó, ezért úgy kapjuk meg az elemek 95%-át tartalmazó tartományt, ha az eloszlások mindkét végéről elveszek 2,5 – 2,5%-ot. A t-eloszlás esetében 3-at adtam meg a szabadsági fokok számának, azaz úgy számoltam, mintha négyelemű mintákat vettem volna a sokaságból.
A görbék kirajzoltatásához nem a ’geom_function()’, hanem a ’stat_function()’ függvényt használtam. A ’stat_function()’ függvény most azért előnyösebb, mert ennek az alkalmazásával nemcsak vonal-, vagy pontdiagramként, hanem területként is lehet ábrázolni egy függvényt, illetve megadható azon x-értékeknek a tartománya, amelyben a függvényt ábrázolni akarjuk. A paraméterek közül ki szeretném emelni a ’geom = line„’ illetve a ’geom = „area”’ paramétereket, mert ezekkel meg tudom adni, hogy a függvénygörbe milyen módon legyen ábrázolva. A másik ilyen fontos paraméter az ’xlim = c(-5, ciN95.1)’, amely megadja azt a tartományt, ahol a függvénygörbét ábrázolni kívánom. Ha megfigyeled a programkódot, akkor látható, hogy a diagramot tulajdonképpen egy vonaldiagramból és két területdiagramból legóztam össze, majd hozzáadtam a diagram címét.
Az utolsó nagy részben a diagramok elhelyezése ugyanazon logikára épül, mint az előző esetben.
Vizsgáljuk meg, hogy különböző mintaelemszámok esetében mekkora az eltérés a t-eloszlás és a normál eloszlás megbízhatósági határai között.
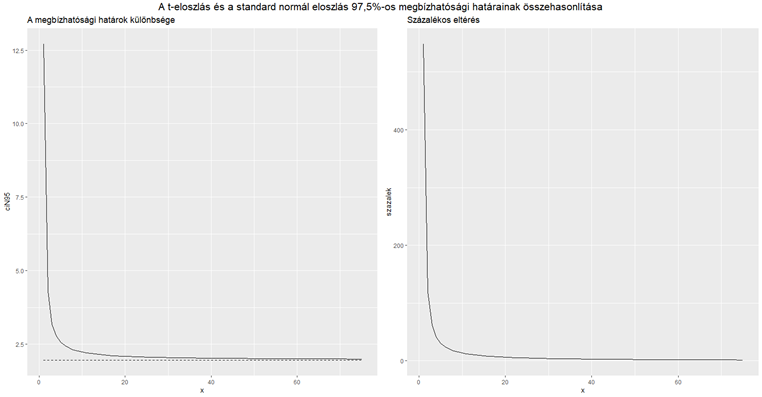
A baloldali diagramon a szaggatott vízszintes vonal a standard normál eloszlás 97,5%-os megbízhatósági határa látható, amely a mintaszámtól függetlenül 1,96. A görbe viszont a t-eloszlás 97,5%-os határait jeleníti meg különböző mintaelemszámok esetén. Látható, hogy 30 körül már egészen kicsi az eltérés, de a t-eloszlás határértéke még 80-nál sem éri el teljesen a normál eloszlás 1,96-ját. A százalékos eltérés a kétféle határérték között 27-nál csökken 5% alá, 31-es mintaelemszám esetén 4,19%, egy 76 elemű minta esetében pedig 1,64%. Ezt a két diagramot a következő módon készítettem el.
#A szükséges csomagok betöltése
library(ggplot2)
library(grid)
library(gridExtra)
#Az eredmények tárolásához szükséges vektorok létrehozása
ciN95 <- c()
ciT95 <- c()
diff <- c()
szazalek <- c()
x <- c()
#A 97,5%-os megbízhatósági intervallumok
#kiszámítása mindkét eloszlás típusra
for (i in 1:75)
{
x[i] <- i
ciN95[i] <- qnorm(p = 0.975, mean = 0, sd = 1)
ciT95[i] <- qt(p = 0.975, df = i)
diff[i] <- ciT95[i] - ciN95[i]
szazalek[i] <- diff[i] / ciN95[i] * 100
i <- i + 1
}
#A két eloszlás 97,5%-os megbízhatósági határainak különbsége
plot1 <- ggplot() + xlim(1, 75) +
geom_line(aes(x = x, y = ciN95), linetype = "dashed") +
geom_line(aes(x = x, y = ciT95)) +
labs(title = "A megbízhatósági határok különbsége")
#A kétféle eloszlás megbízhatósági határainak különbsége százalékosan
plot2 <- ggplot() + xlim(1, 75) +
geom_line(aes(x = x, y = szazalek)) +
labs(title = "Százalékos eltérés")
#A két diagram elhelyezése egymás mellett
grid.arrange(top = textGrob("A t-eloszlás és a standard normál eloszlás 97,5%-os megbízhatósági határainak összehasonlítása",
gp=gpar(fontsize=16,font=1)),
plot1, plot2, ncol = 2)
#Százalékos eltérérek meghatározása a cikkhez
szazalek[26]
szazalek[30]
szazalek[75]
A szükséges csomagok betöltése után létrehoztam azokat a vektorokat (vagy tömböket), amelyekben a számítások adatait fogom tárolni. A tömbök helyett létrehozhattam volna egy adattáblát is a megfelelő mezőkkel, szóval nem ez a feladat egyetlen helyes megoldása. Ezután elvégeztem a diagramok megrajzolásához szükséges adatok kiszámítását.
- Az ’x’ nevű tömbben tárolom le a szabadsági fokok számát 1-től 75-ig. A legegyszerűbb az volt, hogy az ’x’ i-dik elemét egyenlővé tettem i-vel.
- A ’ciN95’ vektorba 75-ször elmentettem a standard normál eloszlás sűrűségfüggvényéhez tartozó x-értéket, amely az elemek 97,5%-át tartalmazza. Ez tulajdonképpen ugyanaz, mintha a vektorba 75-ször elmentettem volna az 1,96-ot.
- A ’ciT95’ vektor viszont a t-eloszlás megfelelő szabadsági fokához tartozó sűrűségfüggvény azon értékét tartalmazza, amelybe az elemek 97,5%-át tartalmazza.
- A ’diff’ tömbben van benne a ’ciT95’ és a ’ciN95’ tömbök összetartozó elemeinek különbsége lett letárolva, vagyis a ’ciT95’ tömb minden eleméből kivontam 1,96-ot.
- A ’szazalek’ tömbben pedig a ’diff’ és a ’ciN95’ tömbök hányadosának százalékos értékei vannak, amely természetesen megadja, hogy a t-eloszlás 97,5%-os határértéke hány százalékkal nagyobb, mint a normál eloszlásé.
Ezután a diagramok kirajzolása már a korábbiakhoz hasonló módon történik. A kód legvégén egyszerűen kiíratom a százalék tömb fent idézett értékeit.
Lassan ugyan, de eljutottunk a cikk legegyszerűbb részéig, az egymintás t-próba végrehajtásáig. Ez nagyon hasonlít az egymintás Z-próba (Senki többet harmadszor? – Újra az egymintás Z-próbáról, most R-kóddal) végrehajtásához. Vagyis ismét a BSDA csomagot fogjuk alkalmazni, csak ez esetben egy másik függvényt.
#A szükséges csomagok betöltése
library(BSDA)
library(psych)
#15 elemű minta létrehozása
minta <- rnorm(15, mean = 10, sd = 3)
describe(minta) #A minta tulajdonságai
#A 15 mintaelemszámhoz tartozó 97,5%-os határérték kiszámítása
myDf <- qt(0.975, df = 14)
#Egymintás t-próba - nullhipotézis elfogadva
t.test(x = minta, mu = 11)
#Egymintás t-próba - nullhipotézis elutasítva
t.test(x = minta, mu = 13)
Ez a kód jelentősen egyszerűbb, mint a korábbiak, ez esetben egyszerűen létrehoztam egy normál eloszlású véletlenszámokból álló tömböt, majd a ’describe()’ függvény segítségével kiíratom a minta jellemző tulajdonságait („Six Sigma in R” sorozat – Leíró statisztika R-ben). Ezután alkalmaztam a ’t.test()’ függvényt a t-próba végrehajtásához. És most lássuk az eredményeket.
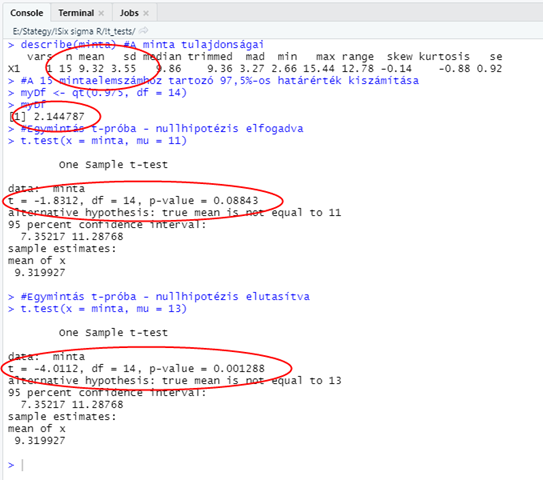
A ’describe()’ függvény által felsorolt statisztikák között most kiemelten fontos a mintaszám (n), az átlag (mean) és a szórás (sd) értéke, a t-próba függvény ezeket fogja felhasználni a ’t’ próbastatisztika kiszámításához (Z helyett t – leheletnyi különbség). A következő két szakaszban pedig egy-egy t-próba eredményt látunk. Az első esetben mű (μ) értéke 11, ez egy olyan potenciális sokaság átlaga, amelyből a létrehozott mintát kivehettük. Ez esetben a ’t’ próbastatisztika értéke -1,8312 (a 9,32 – 11 különbség miatt lett negatív). A 15 elemű mintához 14-es szabadsági fok tartozik. Az ehhez tartozó t-próba határérték 2,144, vagyis a kapott próba statisztika abszolút értéke értéke kisebb, mint a t-próba határérték, vagyis a nullhipotézis elvetéséhez nincs elegendő bizonyítékunk.
A második esetben azt feltételeztük, hogy a mintát egy olyan sokaságból vettük ki, amelynek az átlaga 13. Ez esetben azt kaptuk, hogy a t próba statisztika értéke -4,0112. Ennek az abszolút értéke jóval nagyobb, mint a t-próba határértéke (2,144), így a nullhipotézist elvethetjük és elfogadjuk az ellenhipotézist, mely szerint a mintát nem vehettük ki egy olyan sokaságból, amelynek az átlaga 13.
De a történet ezzel még mindig nem ér véget. Egy korábbi cikkben (És mégis miért kellene normálisnak lennie?) már fejtegettem egy soron, hogy vajon milyen feltételek mellett alkalmazható az egymintás Z-próba. A nagyszámú minta miatt ott igazából ez nem volt túl izgalmas kérdés. Az egymintás t-próba esetében viszont sajnos nem dőlhetünk hátra hasonló módon. A minták alacsony számának köszönhetően ez esetben a mintaátlagok nem feltétlenül lesznek normál eloszlásúak. Egy erősen aszimmetrikus eloszlású sokaság esetében a mintaátlagok eloszlása is hasonlóan aszimmetrikus lesz, emiatt a t-eloszlás alkalmazásával kapott eredmények nem lesznek pontosak, hiszen fentebb már tisztáztuk, hogy a student-eloszlás szimmetrikus jellegű. Has mutassam meg ezt egy példán keresztül is.
#A szükséges csomagok betöltése
library(ggplot2)
library(ggpubr)
library(grid)
library(gridExtra)
#Aszimmetrikus sokaság létrehozása
sokasag <- rexp(10000, rate = 1)
#2-elemű minták átlagainak kiszámítása
mintaAtlagok2 <- c()
for (i in 1:1000)
{
minta <- sample(sokasag, 2, replace = FALSE)
atlag <- mean(minta)
mintaAtlagok2[i] <- atlag
i <- i + 1
}
#2-elemű minták átlagainak ábrázolása
gghistogram(mintaAtlagok2, bins = 32)
Ezt a kódot most már nem magyaráznám el részletesen, itt semmi olyat nem csináltam, amelyet nem írtam volna le részletesen korábban. A lényeg az eredmény. Ha kiveszünk rengeteg kételemű mintát egy erősen aszimmetrikus sokaságból és ábrázoljuk ezek eloszlását, akkor jól látható, hogy a mintaátlagok eloszlása is aszimmetrikus lesz.

Ahogy emeljük a minták elemszámát, úgy csökken az aszimmetria, de nem múlik el teljesen.
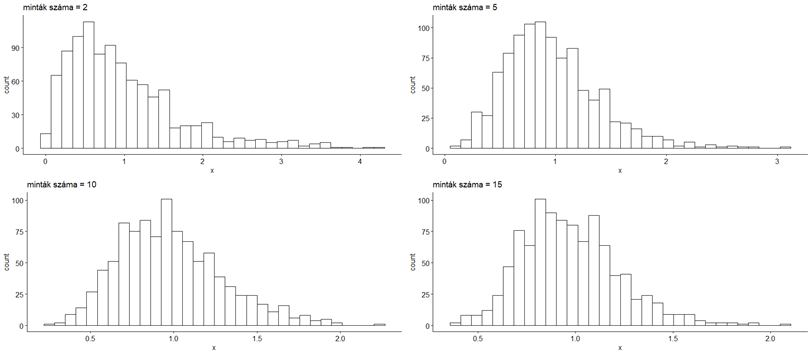
Emiatt sajnos ez esetben tényleg feltételeznünk kell, hogy a sokaság normál eloszlású, vagy legalábbis szimmetrikus eloszlású, különben tényleg hibás döntést fogunk hozni. De ez még mindig csak egy feltételezés és nem tény, mert a sokaság eloszlását nem tudjuk ellenőrizni. A minta eloszlását tudjuk ellenőrizni, bár a nagyon kicsi mintaszámok esetében ennek nem sok értelme van. Végig gondolva az egészet, leginkább azt tudom javasolni, hogy ha a sokaság jellegéből adódóan sejtjük, hogy az nem normál eloszlást követ, akkor sajnos ez a teszt nem alkalmazható, más megoldást kell keresnünk a kérdés megválaszolására. Ilyen lehet például valamilyen nem-paraméteres teszt alkalmazása, mint például a Wilcoxon-féle rangteszt (Pszichológus hallgatóknak közkívánatra – Wilcoxon-féle előjeles rang teszt a medián vizsgálatára (Wilcoxon signed rank test for a median)), de ennél például legalább azt kell feltételeznünk, hogy a sokaság szimmetrikus. Legvégső esetben szóba jöhet a megbízhatósági intervallum meghatározása ún. "bootstrap" módszer alkalmazásával, amely tulajdonképpen nagyszámú visszatevéses minta átlagai alapján adja meg azokat a határértékeket, ahol a mintaátlagok 95 vagy 99 százaléka található. Viszont a minta eloszlásának vizsgálata ebben az esetben is nagyjából szükségtelen.
Összegzés:
A cikkben megpróbáltam az egymintás t-próbát a lehető legrészletesebben bemutatni és ebben az R programozási nyelv nagy segítségemre volt, mert egy csomó olyan diagramot is el tudtam készíteni, amelyeket eddig eszembe sem jutott volna. Remélem, hogy sikerült egy minden szempontból érthető és követhető leírást adnom erről a tesztről.
A cikkben ismertetett R-kódokat le tudod innen tölteni.






