
A napokban segítséget kért tőlem egy kedves pszichológus hallgató egy témában, majd miután azt megbeszéltük felvetette, hogy lenne itt még egy téma, amelyben segítségre szorulna a csapata. Bár eredetileg nem ezzel akartam foglalkozni, úgy gondoltam, hogy megpróbálok segíteni a csapatnak a következő ZH-ra való felkészülésben.
A probléma, amelyet felvetett, tulajdonképpen egy táblázatban volt összefoglalva:

Vagyis az volt a kérdés, hogy milyen hipotézis vizsgálatokkal lehet vizsgálni az olyan adatsorok középértékeit, amelyek elemszáma kicsi, viszont nem normális eloszlásúak. A kérdés konkrétabban az volt, hogy mit takarnak a „Mivel” oszlopban jelölt „titkos kódnevek”. Az egymintás t-próbával már én is foglalkoztam korábban (A sörfőző, aki forradalmasította a statisztikát, illetve Hogyan csináld Minitab-bal – Egymintás t-próba), de a nemparaméteres próbákat még nem vettem sorra. Ráadásul az oszlopban szereplő többi név nem sokat mond nekem sem (mondjuk erre nem vagyok büszke). De úgy döntöttem, hogy felveszem a kesztyűt és beleállok a kihívásba. Azt nem ígértem, hogy sorban fogok menni, ezért most a ’Wilcoxon Signed Rank Test for a Median’ című – számomra teljesen semmitmondó nevű – módszert fogom bemutatni. A magyar neve még unalmasabb és még véletlenül sem derül ki belőle, hogy mire való. Szokásosan újra felmérgeltem magam és megpróbálom a hozzám hasonló földi halandók számára is érthető nyelven leírni, hogy mi is ez valójában.
Ezt a tesztet egy Frank Wilcoxon nevezetű úriember találta ki 1945-ben és ez volt a statisztika történetében az egyik első nem paraméteres (non-parametric) teszt, ami azt jelenti, hogy nincs különösebb megkötés a vizsgált adatsor eloszlásával kapcsolatban. A próba alkalmazásának csak két feltétele van:
- A vizsgált változó folytonos legyen
- Az adatsor eloszlásának sűrűségfüggvénye szimmetrikus legyen
A teszt célja az, hogy megállapítsa, hogy a vizsgált véletlenszerű minta mediánja megegyezik-e egy sokaság feltételezett mediánjával. Ez alapján a feltételezett nullhipotézis a következő:
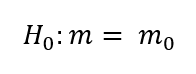
Az ellenhipotézis ennek megfelelően
![]()
vagy egyoldali ellenhipotézis esetében
![]()
De miért a mediánt vesszük alapul és miért nem az átlagot? Amikor az adatsorok középérték mérőszámairól volt szó (Adathalmazok középértékeinek mérőszámai), akkor megemlítettem, hogy az átlag nagyon érzékeny a kieső értékekre, a mediánnak viszont nincs meg ez a tulajdonsága. Amíg a vizsgált adatsor normál eloszlású, addig igazából mindegy, hogy az átlaggal vagy a mediánnal számolunk, ha viszont az adatsor eloszlása ferde vagy nem szimmetrikus, akkor a medián jó eséllyel jobb becslést ad az adatsor középértékére, mint az átlag vagy a módusz.
A példában fekete törpesügérek (lásd a fenti képet) véletlenszerűen kiválasztott egyedeinek hosszát vizsgáljuk. A kiválasztott halak méretei a következők:
5,0 ; 3,9 ; 5,2 ; 5,5 ; 2,8 ; 6,1 ; 6,4 ; 2,6 ; 1,7 ; 4,3
A kérdés az, hogy vajon a törpesügérek hosszainak mediánja jelentősen eltér-e 3,7-től?
Ennek a kérdésnek az eldöntéséhez létre kell hoznunk egy táblázatot. A táblázat első oszlopa egy sorszám lesz, a második oszlopába pedig begépeltem a fenti adatokat.

Első lépésként ki kell számolnunk minden egyes érték esetében, hogy milyen távolságra vannak a megadott ’m0’ mediántól. Ez ismerős történet, a blog kezdetén az adatsorok szóródásának ismertetésekor (Adathalmazok elemeinek szóródása - A szórás és a variancia) jött elő ugyanez, csak akkor az átlagot vettük az adatsor középértékének, nem pedig a mediánt.
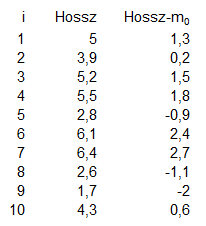
Viszont itt is fennáll az a probléma, hogy az eltérések egy része nagyobb nullánál, másik része viszont kisebb. Annak érdekében, hogy az adatsor elemeit sorba tudjuk rendezni aszerint, hogy milyen távolságra vannak a mediántól, vegyük ezeknek a távolságoknak az abszolút értékét:
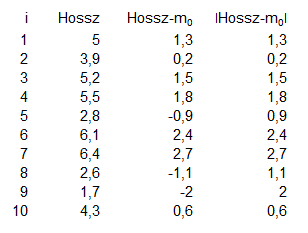
Ok, akkor most rendezzük nagyság szerint növekvő sorrendbe a ’Hossz’ és az ’m0’ különbségeinek abszolút értékeit és írjuk oda mindegyik adat mellé, hogy ő éppen hányadik a rangsorban. Például a negyedik oszlopban az 1,3 az ötödik legkisebb távolságra van a mediántól, ezért ő az ötös sorszámot, a 0,2 pedig a legkisebb távolságra van, ezért ő pedig az egyest kapja. Ezt nem bonyolítottam túl, átrendeztem a táblázatot a negyedik oszlop alapján növekvő sorrendbe, kitöltöttem a ’Rang (Ri)’ mezőt sorszámokkal, majd az egész táblázatot visszarendeztem az első oszlop szerint növekvő sorrendbe.
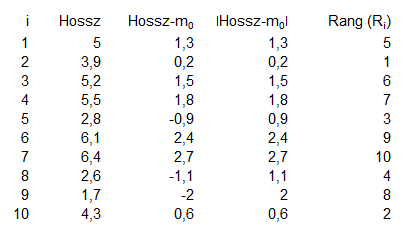 Azért, hogy hűek legyünk a teszt nevéhez, generálunk egy olyan oszlopot, amely az előzőleg meghatározott rangokat tartalmazza, de úgy, hogy ahol a ’Hossz’ távolsága a mediántól negatív volt, ott a ’Rang’-ot megszorozzuk -1-gyel. Hogy ennek mi értelme van, azt nem igazán értem, mert a továbbiakban a negatív értékeket nem fogjuk felhasználni. Mondjuk arra fel lehet ezt használni, hogy a SZUMHA() függvénnyel excelben össze lehet adni azokat a számokat, amelyek nagyobbak nullánál.
Azért, hogy hűek legyünk a teszt nevéhez, generálunk egy olyan oszlopot, amely az előzőleg meghatározott rangokat tartalmazza, de úgy, hogy ahol a ’Hossz’ távolsága a mediántól negatív volt, ott a ’Rang’-ot megszorozzuk -1-gyel. Hogy ennek mi értelme van, azt nem igazán értem, mert a továbbiakban a negatív értékeket nem fogjuk felhasználni. Mondjuk arra fel lehet ezt használni, hogy a SZUMHA() függvénnyel excelben össze lehet adni azokat a számokat, amelyek nagyobbak nullánál.
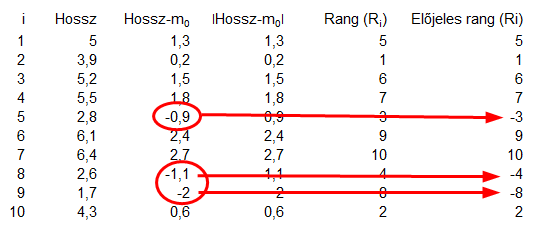
Ennek annyiban van értelme, hogy a teszt további részében csak azokkal a rangokkal fogunk tovább dolgozni, amelyek esetében a ’Hossz’ távolsága a mediántól pozitív érték. Gondolom ezért kell szimmetrikusnak lennie az adatok eloszlásának, hiszen a teszt csak a pozitív irányú szóródásokkal számol. Ezt egyébként más módszerrel úgy lehet elérni, hogy definiálunk egy ’Zi’ változót, amelynek az értéke 0, ha a ’Hossz’ távolsága a mediántól negatív és 1, ha ez a távolság pozitív. Ezek után összegezni lehet az ’RiZi’ szorzatot, így megkapjuk W értékét.
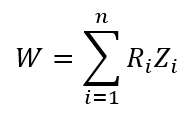
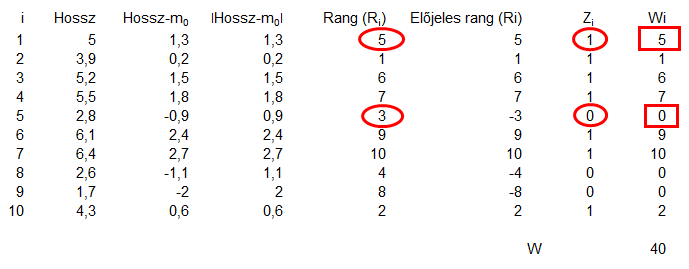
Így megkaptuk a próba statisztikáját. Most pedig meg kellene határozni azt a határértéket, amelynek a segítségével el tudjuk dönteni, hogy az adatsor mediánja megegyezhet-e a feltételezett ’m0’ értékkel, azaz 3,7-tel. Ehhez viszont tudnunk kellene, hogy W milyen eloszlású!
A W próba statisztika eloszlásának megértéséhez egy kis kitérőt kell tennünk. Mivel W lehetséges értékei diszkrét adatok lesznek a rang meghatározásának logikája miatt, ezért a W határérték meghatározása is más lesz egy kicsit, mint a szokásos. Először is nézzük meg, hogy mi lehet a lehetséges legkisebb érték, amelyet W felvehet. W definíciójából adódóan ez nulla lesz, hiszen, ha a minta összes eleme kisebb, mint az általunk megadott ’m0’ medián értéke (ne felejtsük el, hogy m0 nem a minta saját mediánja, hanem az általunk megadott érték), akkor az összes elem eltérése negatív lesz, így W kiszámításakor egyik sem lesz figyelembe véve.
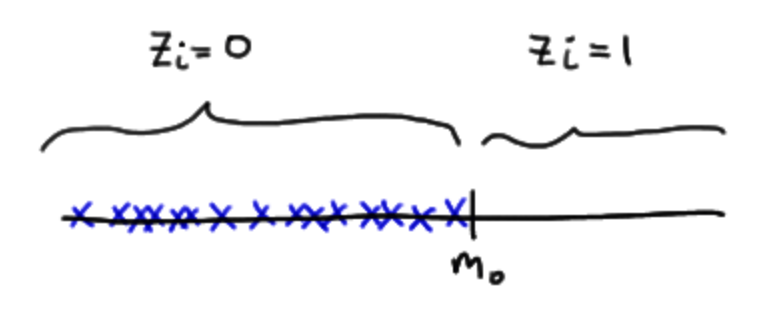
És mi a legnagyobb érték, amelyet W felvehet? Ez akkor fordulhat elő, ha a minta összes eleme nagyobb, mint a megadott ’m0’ határérték. Ekkor az összes adatelem távolsága pozitív és így figyelembe vannak véve W kiszámításakor.

Mivel W kiszámításakor az adatok sorszámát adjuk össze (és ’Zi’ minden esetben 1 lesz), ezért W-t a következő módon kapjuk meg:
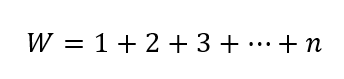
Ha vesszük ezeket a természetes számokat és összepárosítjuk őket a következő módon, akkor azt kapjuk, hogy

Azaz páros számú elem esetében minden egyes pár értéke 7, azaz n+1 lesz és n/2 darab ilyen párt fogunk kapni. Páratlan számok esetében hasonló a logika, nézzük meg:

Itt is n+1 lesz a párok összege, de n/2-1 darab pár fog keletkezni. Viszont van egy plusz „fél pár”, amelynek az értéke pontosan (n+1)/2. Így hogyan is alakul az összeg:
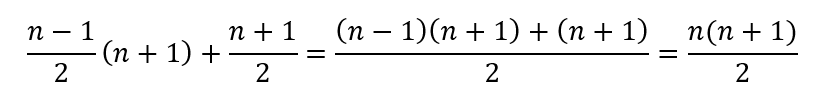
Vagyis, ha a számlálóban van n-1 darab n+1 összegünk és ehhez hozzá adunk még egyszer n+1-et, akkor n darab n+1 összegünk lesz, azaz ugyanúgy szépen megkapjuk a fenti összefüggést. Ezek alapján elmondhatjuk, hogy W egy diszkrét véletlen változó, amelynek az értékei 0 és n(n+1)/2 értékek között változhat.
Lépjünk még egyet előre. Tegyük fel, hogy n=2, vagyis az adatsorunk két elemből áll, az 1-ből és a 2-ből. Ekkor W milyen értékeket vehet fel attól függően, hogy az 1 vagy a 2 pozitív, vagy negatív előjelű?
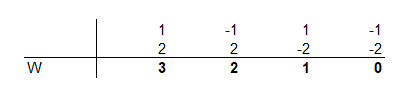
Mint látható W értéke egyforma valószínűséggel vehet fel 0-t, 1-et, 2-őt vagy 3-at. Azaz elegendően nagyszámú minta esetében annak a valószínűsége, hogy ezek közül a számok közül bármelyiket felveszi egyforma, konkrétan 1/4, vagy 0,25.
Mi történik akkor, ha a mintánk három elemű?
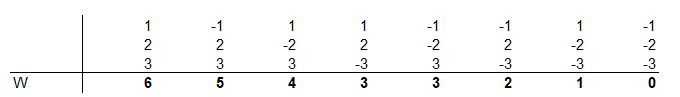
Ekkor már 8 különböző kombinációnk lehetséges, amelyeknek az eredménye 0 és 6 között vehet fel értékeket. Mint látható, a 3 kétféle módon is kijöhet, így a 3 előfordulásának a valószínűsége elegendően nagy számú kísérlet esetében 2/8, míg az összes többi szám 1/8 valószínűséggel jöhet ki.
És ha 4 elemű mintánk van?
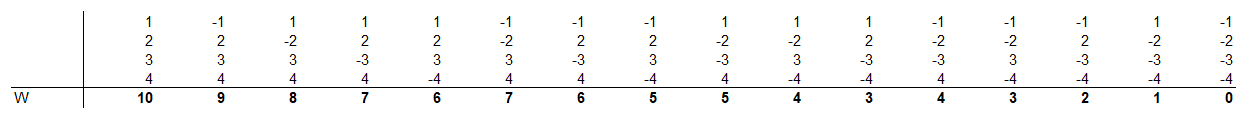
Itt hányszor jönnek ki a különféle értékek?
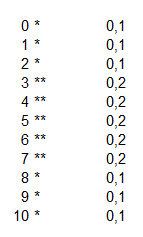
Amint látható, a 0, az 1 és a kettő, valamint a 8, a 9 és a 10 csak egyszer fordulnak elő, de a 3, a 4, az 5, a 6 és a 7 kétféleképpen is kijöhetnek. Akkor most növeljük meg a minta elemeinek a számát még eggyel:
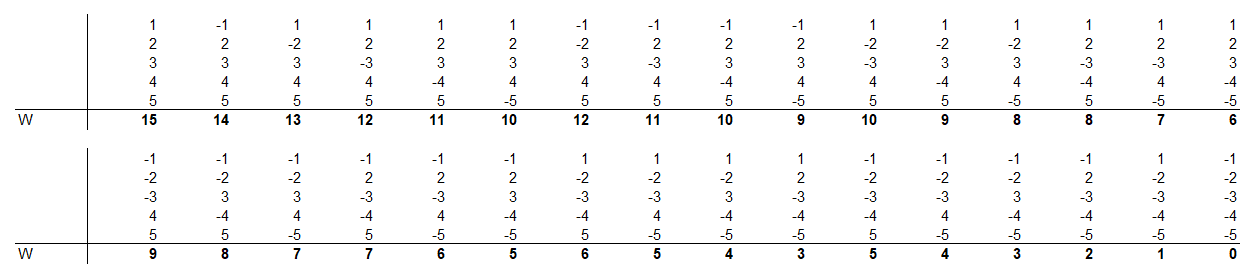
Az egyes W értékek gyakoriságát újra megvizsgálva hasonló eredményt kapunk. Itt is megfigyelhető, hogy a szélső értékek kevesebbszer, míg a középen lévők egyre gyakrabban jelennek meg. ennek az az oka, hogy a középen lévő értékek többféle kombinációban is kiadódhatnak.

Jé, ez ismerős valahonnan! Korábban már készítettem egy hasonló kísérletet dobókockákkal (Miért fordul elő a normál eloszlás olyan gyakran a természetben?), ahol igencsak hasonló eredmények jöttek ki. Vagyis feltételezhetjük, hogy eléggé nagy n esetében W gyakoriságai normál eloszlást követnek. Ha n értéke kicsi, akkor sem kell megijednünk attól, hogy a fenti gyakorlatsort minden esetben végig kell csinálnunk, szerencsére 4-től 12-ig valaki már elvégezte helyettünk az aprómunkát és készített egy táblázatot a keresett valószínűségekről:


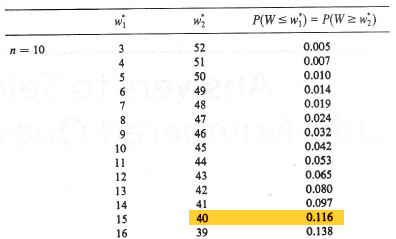
Hogyan kell használni a fenti táblázatot? A táblázat bal oldalán található n értéke, majd a következő két oszlopban találhatók az adott n-hez tartozó W értékek szélső tartományai, vagyis a ’w1*’ oszlop azokat a valószínűségeket tartalmazza, ha W kicsi, a ’w2*’ oszlop pedig azokat, amikor W értéke nagy. A harmadik oszlopban a P-value értékei találhatók. Ha kikeressük a W kiszámított értékét az adott n-hez tartozó táblázatban, akkor a hozzá tartozó P-érték megadja, hogy mekkora a valószínűsége annak, hogy W ilyen vagy ennél szélsőségesebb értéket vesz fel. Ezt a P-értéket fogjuk hasonlítani a próba során kiválasztott megbízhatósági határértékkel (0,05 vagy 0,01). Ha a P-érték nagyobb, mint a megbízhatósági határérték, akkor a nullhipotézist elfogadjuk, ha kisebb, akkor pedig elutasítjuk. Egy dologra kell feltétlenül odafigyelnünk: Mivel a teszt során a minta eloszlásának csak a pozitív oldalát figyeljük, viszont a hipotézis vizsgálat kétoldalas, ezért a P-értéknek mindig a kétszeresét kell vennünk.
Nézzük meg ezt a fenti példánkon:
Mivel 10 darab fekete törpesügér adata áll rendelkezésre, ezért n = 10, vagyis a táblázatnak ezzel a részével fogunk dolgozni. Itt ki kell keresnünk a fentebb kapott W = 40 értéket. Meg is találtuk, az ehhez tartozó valószínűség 0,116. Ezt még meg kell szoroznunk kettővel, így 2 x 0,116 = 0,232 jön ki P értékére. Ez jóval nagyobb, mint az eredetileg kiválasztott 0,05, ezért a nullhipotézist elfogadjuk, azaz a minta által reprezentált sokaság mediánja lehet 3,7.
Elegendően nagyszámú minta esetében (szerintem ez több, mint 30 értéket jelent, mert ez a módszer a Centrális Határeloszlás tételére épül) egy más módszerrel kell megközelítenünk a történetet. Ekkor W’-t a következő képlet segítségével számíthatjuk ki:
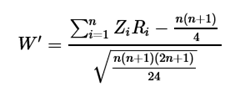
Ha W-t ezzel a képlettel számítjuk ki, akkor W1 standard normál eloszlást követ (Első az egyenlők között – A standard normál eloszlás). Hurrá, akkor ez esetben elfogadási kritériumként használhatjuk a standard normál eloszlásnak az egymintás Z-próba (Z, mint Z-próba – Egymintás) során megismert megbízhatósági határértékeket:

Összegzés: Elsőre nem feltétlenül volt világos számomra a teszt nevének a jelentősége, de a részletes feldolgozás során egy kicsit „megvilágosodtam”. A „rang” jelző nyilvánvalóan arra utal, hogy a próba során a „rangjuk” alapján sorba rendezi a minta elemeit és ezeket a rangokat használja fel a próba statisztika kiszámításához. A W határérték kiszámítása – valószínűleg pont emiatt – egy kicsit kacifántosabb, mint a szokásos, de nem lehetetlen feladat. Sajnos a mellékelt táblázat csak n = 12-ig tartalmazza a keresett valószínűségeket, a W’ képlet viszont (szerintem) csak 30 darabos minták felett alkalmazható. Hogy mit lehet tenni a 13 és 29 közötti elemszámú mintákkal? Hmm, valószínűleg nincs más út, mint a fent ismertetett módon végig venni a lehetséges kombinációkat és kiszámolgatni a gyakoriságokat…
Forrás: The Wilcoxon Signed Rank Test for a Median, Penn State University – STAT 414 / 415 - https://newonlinecourses.science.psu.edu/stat414/node/319/





