Továbbra is futom a köreimet a kísérlettervezési módszerek körül. Ebben a cikkben egy olyan kísérlettervezési módszert mutatok be, ami elsőre lenyűgözött az egyszerűségével, majd pedig azzal, hogy mennyire nehéz volt rájönni, miért működik. Azt egyébként nem mondanám, hogy ez egy mainstream alkalmazás, életemben nem hallottam még róla – egészen mostanáig.
Pusztába kiáltott szó – Minőségbiztosítással kapcsolatos podcastok a világban
Minőségbiztosítás

A podcast egy divatos műfaj. Minőségbiztosítási szakemberként érdekel, hogy milyen a választék a podcast-piacon ebben a témában. Hát, szűkös…
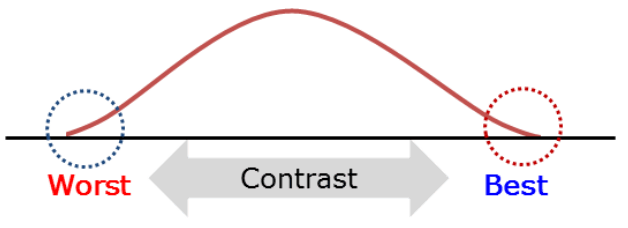
Előtte és utána – Shainin B vs C teszt
Problémamegoldás

Amikor fejlesztünk valamit, akkor vagyunk elégedettek, ha látjuk a változást. Vannak olyan változások, amelyek szabad szemmel is jól láthatók, más esetekben talán nem teljesen egyértelmű a változás, ezért szükségünk lehet valamilyen bizonyítékra annak eldöntése érdekében, hogy eldöntsük, vajon van-e hatása annak, amit csináltunk. Manapság erre a kétmintás t-próbát szoktuk alkalmazni. Ez sem túl bonyolult manapság a számítógépek és a szoftverek világában, de azért sokan vannak olyanok, akiknek még ez is sok, ha statisztikáról van szó.
Kísérlettervezés kifejezetten mérnököknek – Taguchi-féle kísérlettervezés
Problémamegoldás

Ebben a cikkben visszatérek a kísérlettervezéshez, azonban ez alkalommal egy más stílusú kísérlettervezési módszert szeretnék bemutatni.
Az elakadt számláló – Műszaki probléma megoldása Shainin component search segítségével
Problémamegoldás

Előző írásomban (Keresztpróba felsőfokon – Shainin Component Search Principle) bemutattam a keresztpróbák luxuslimuzinját, de csak elméletben. Most nézzük meg, hogyan működik ez a módszer a gyakorlatban.
Keresztpróba felsőfokon – Shainin Component Search Principle
Problémamegoldás
A problémamegoldás keresztpróbával, azaz egy jó és egy hibás szerelvény alkatrészek szisztematikus cserélgetése a hibát okozó alkatrész megtalálása érdekében, nem egy űrtechnika. A módszer Shainin-féle változata azonban rádöbbentett arra, hogy mennyire rosszul csináltam ezt eddig.
A 80-as évek óta csak felejtünk... - Taguchi veszteségfüggvénye
Minőségbiztosítás
Innen a 2020-as évekből visszatekintve úgy tűnik, hogy a 80-as évek a minőségfilozófiák egyfajta aranykora volt. Szerencsére most már egészen sok eredeti videót lehet találni a youtube-on ebből a korszakból, ezek közül kettőről már írtam korábban („Ha a japánok tudják, mi miért nem?” – W. Edward Deming igaz története). Most egy másik hasonló videót szeretnék bemutatni.
E pluribus unum, azaz sokból egy – A Hotelling T2-kártya
Statisztikai folyamatszabályozás

A címválasztás nem véletlen. Ez a latin kifejezés több szempontból is telitalálat a következő cikk témájával kapcsolatban. Az egyik ok az, hogy noha ez az Amerikai Egyesült Államok egyik első és nagyon híres jelmondata, amely egyébként a különféle dollár bankjegyeken és a váltópénzeken is szerepel, nem biztos, hogy sokan emlékeznek rá, hogy mit is jelent. A másik okom pedig a kifejezés jelentése volt, ugyanis a cikk témájául választott Hotelling T2-szabályozó kártya pontosan ezt teszi: Sok SPC-kártyából csinál egyet!
Árnyjáték – A Főkomponens elemzés (Principal Component Analysis)
Statisztikai elemzések

A főkomponens elemzés (Principal Component Analysis) röviden összefoglalva egy árnyjáték, ahol egy bonyolult térbeli alakzat árnyképét úgy próbáljuk rávetíteni egy síkfelületre, hogy közben az alakzat jellegzetes tulajdonságaiból minél kevesebbet veszítsünk el. Csak éppen ez a térbeli alakzat nem feltétlenül háromdimenziós. Lehet, hogy négy-, vagy ötdimenziós, vagy még több…
A módszer matematikai megvalósítása tele van mátrixműveletekkel. Ennek oka, hogy a módszer alapja a lineáris algebra világába vezet és igényli néhány elvont fogalom megértését is, úgymint az sajátvektorok (eigenvectors) és a sajátértékek (eigenvalues). Akit érdekel annak javaslom, hogy keresse fel Sajó Zsolt Attila oldalát, aki bevezet a főkomponens elemzés elméleti matematikai hátterébe.
https://sajozsattila.home.blog/2021/08/02/fokomponens-analizis-2/
NYÁRI SZABADSÁG

Szia,
Most szeretnék szusszanni egyet, de szeptembertől természetesen újabb bejegyzésekkel fogom majd színesíteni a blogot. Természetesen az eddig megjelent írások ebben az időszakban is elérhetők.
Kösz a türelmet