 (A képre kattintva megnyílik az előző bejegyzés)
(A képre kattintva megnyílik az előző bejegyzés)
A német tank problémáról szóló bejegyzés után az olvasók egy része hitetlenkedett, véleményük szerint a leírt módszer megbízhatatlan. Mivel ez a kritika sokszor elhangzott, ezért engem is elkezdett foglakoztatni a kérdés, hogy hogyan lehetne igazolni a módszer megbízhatóságát. Először arra gondoltam, hogy ismét készítek egy csomó minta adatsort és ezeken tesztelek, de aztán egyszer csak jött az ötlet, hogy tulajdonképpen van egy szabadon hozzáférhető hatalmas adathalmaz, amelynek létrehozásakor egymás után szépen sorbarendezett számok halmazából választanak ki véletlenszerűen öt vagy hat számot. Igen, a lottószámok!
Fogalmam sincs, hogy valaha bárki is használta-e ezt a rengeteg adatot így, hogy én tervezem, mert ez most nem a klasszikus lottószám elemzés lesz. Most nem azt nézem, hogy melyik lottószám milyen gyakran került kihúzásra, hanem azt fogom megvizsgálni, hogy az öt kihúzott szám alapján mennyire pontosan tudom megbecsülni azt, amit amúgy is tudunk: hogy az öt számot 90 darab sorszámozott golyóból választották ki.
Nagy előnye az ötletnek, hogy nem én találtam ki az adatsort, bárki szabadon letöltheti a Szerencsejáték Zrt. weboldaláról és ugyanígy leellenőrizheti az állításaimat. Tehát az adatmanipuláció kizárva!
Szóval megtettem azt, amit az előbb már írtam, letöltöttem az ötöslottó nyerőszámait 1957-től napjainkig tartalmazó excel file-t:
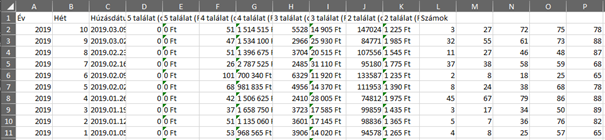
A táblázatban letakartam az engem most kevésbé érdeklő mezőket, illetve a „Becsles” oszlopba elkészítettem a képletet, amit az előző cikkben leírtam. Tehát a kérdés az, hogy az öt véletlenszerűen kiválasztott szám alapján ki lehet-e találni, hogy ezt 90 darab számból választották ki. A táblázat valahogy így néz ki az első simítások után:

Első ránézésre nem túl bíztatóak az eredmények. Van itt minden, de pont 90-et nem nagyon látni. Viszont az eredeti mondás az volt, hogy a képlet egy becslés, tehát ne várjam, hogy pontosan el fogja találni a keresett 90-et. Jó, de mennyire pontatlan a becslésem? Egy adatelemzést én mindig azzal kezdek, hogy lefuttatok ár egy leíró statisztikát. Nézzük meg, mit mutat ez jelen esetben:

Hmm, ez érdekes. A lottószámok statisztikája azt mutatja, hogy a becslések átlaga 89,535, a medián pedig 93,8, tehát mindkettő majdnem megegyezik a keresett 90-nel! Itt azért elkezdtem reménykedni, hogy talán mégsem írtam akkora marhaságot az előző bejegyzésben, mint az elsőre látszott. Viszont a legkisebb és a legnagyobb értékek között nagyon nagy a különbség. A legkisebb érték 27,8? Ez azért kicsit fura. Ezt nézzük meg egy kicsit alaposabban. A medián körül még talán nincs akkora baj. A Q3 és a medián különbsége 7,2 (101 – 93,8), a medián és a Q1 különbsége 12 (93,8 – 81,8), ezek közel azonosak, tehát a medián környezetében szimmetrikus az eloszlás. Ráadásul elég kicsi a távolság a Q1 és a Q3 között, ami azt jelenti, hogy az adatok fele 81,8 és 101 közé esik.
Az eloszlás két vége viszont nagyon eltérő. Ha a maximumból kivonom a Q3-at, akkor 6-ot kapok (107 – 101), ha viszont a Q1-ből kivonom a minimumot, akkor 54-et! Az már biztos, hogy az eloszlásom nem szimmetrikus, tehát nem lehet normál eloszlású. Ezt bizonyítja a normalitásvizsgálat eredménye is, a pontok nem igazán simulnak rá a kék egyenesre.
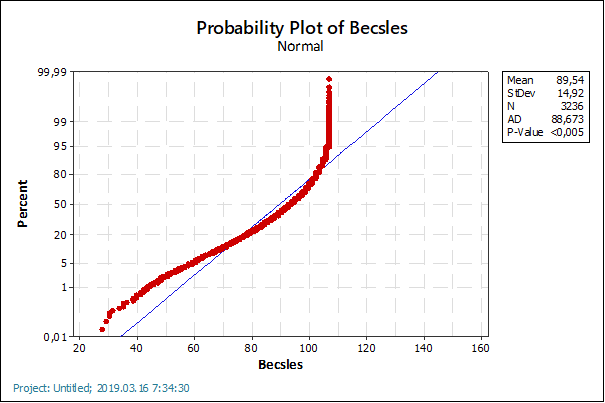
Ellenőriztem, hogy a Q1 és a minimum érték közötti különbség köszönhető-e annak, hogy az adatsor kieső értékeket tartalmaz:

A Grubb's outlier teszttel kicsit óvatonak kell lennem, mert az a normál eloszlásra jellemző tulajdonságok alapján ítélkezik, nekem pedig van egy rossz érzésem ,hogy ez az adatsor nem normál eloszlású. Ezért viszont megpróbálkozom azzal, hogy egy boxplot-tal ábrázolom az adatokat. Ez viszont egy rakás kieső értéket produkál lefelé:

Hurrá! A kétféle teszt kétféle eredményt ad! Ez önmagában még érthető is lenne, hiszen a Minitab a kieső értékek határát a Q3-Q1 alapján számolja (részletesen lásd itt). Szóval ezt már nem tudom hova tenni, tehát jöjjön, aminek jönnie kell: ábrázolom az adatokat.

Ez egy igen érdekes hisztogram. Olyan, mintha egy elnyújtott normál eloszlás görbe lenne 100 körüli mediánnal, aminek levágták a felső részét! Ez akár még logikus is lehet, hiszen 90-nél nagyobb számot nem lehet kihúzni a lottón, tehát az alkalmazott képlet alapján a legnagyobb érték ez esetben 90+(90/5)-1=107,2 lehet. Vagyis van egy képletem, ami egészen jól becsüli a középértéket, azaz a 90-et, de relatíve nagy a szórása. De mennyire nagy? Ahhoz, hogy lemérjem a képlet becslésének megbízhatóságát, megszámoltam, hogy az eredmények közül mennyi esik a 90 körüli ±5%, ±10%, ±15%, és ±20%-os tartományba. Ezt egy kettős HA() függvénnyel végeztem el, készítettem 4 oszlopot az adatoknak, és ha az adott érték a megadott tartományba esett, akkor 1-et, egyébként pedig nullát adtam értékül, valahogy így:
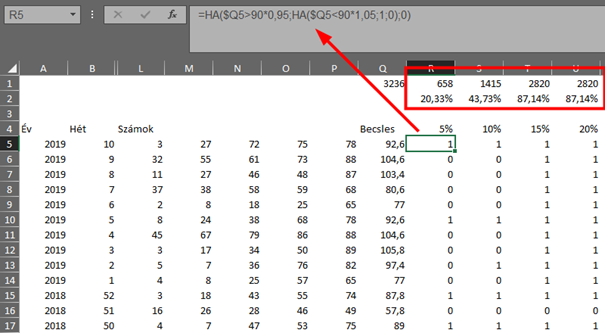
Az eredményekből jól látható, hogy az ötszázalékos tartományba az eredményeknek csak az ötöde került, a tíz százalékosba már 43 százaléka, a 15 százalékosba viszont már az eredmények 87 százaléka került. Érdekes módon a 20 százalékos kategóriában már nem növekedett az ide bekerült elemek aránya. Grafikusan ez valahogy így néz ki:
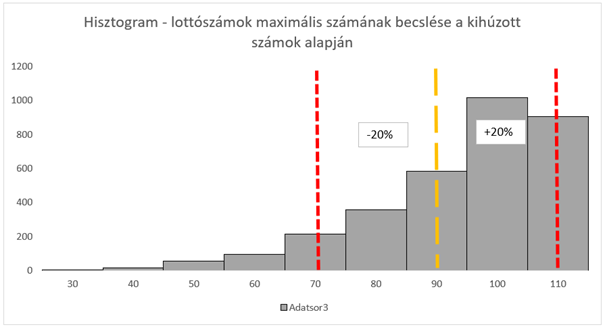
Összefoglalás:
A bejegyzés célja az volt, hogy megállapítsam, mennyire megbízható a német tank probléma megoldásához megadott képlet. Ehhez az ötöslottó nyerőszámait tartalmazó táblázatot használtam fel, megpróbáltam megbecsülni, hogy mennyire lehet eltalálni a 90-et, ahány számból az ötöslottó nyerőszámait kihúzzák.
Az jól látszik, hogy a módszer nem ad tökéletes eredményt. Ennek ellenére a vizsgálat eredménye alapján ki merem jelenteni, hogy a képlet alkalmazása által 87%-os valószínűséggel el lehet találni a valós célszám körüli ±15-20%-os tartományt. Véleményem szerint ez nem is olyan rossz eredmény tekintve, hogy mennyire kevés adatból kell következtetéseket levonni. A nagyságrendi eltéréseket mindenképpen ki lehet vele zárni. Természetesen így is van 13% esély arra, hogy a becslés jelentősen kisebb lesz, mint a célérték, de a hisztogramból az is látható, hogy minél nagyobb a becslés eltérése a valós értéktől, annál kisebb a valószínűsége annak, hogy ez bekövetkezik.
Végezetül egy megjegyzés az eredeti problémához. Az eredeti dokumentumokból kiderül, hogy a becsléseket nem egyetlen adatból (pl. a sebességváltó ház típustábláin szereplő adatokból) állapították meg, hanem a tankokból összeszedhető egyéb adatokból és információkból kialakított komplex elemzés alapján. Ezek alapján a sztori számomra még mindig hihető.




