Korábban már foglalkoztam a különféle adathalmazok átlagainak összehasonlításával (Z, mint Z-próba…egymintás! vagy Z helyett t – leheletnyi különbség, illetve Az alkoholfogyasztás hatása a bowling eredményekre – kétmintás t-próba). Ezekben az esetekben azonban nem foglalkoztam az adathalmazok elemeinek szóródásával. És itt fel lehet tenni azt a kérdést, hogy ha két adatsor átlaga megegyezik, akkor kijelenthetjük-e lelkiismeretfurdalás nélkül, hogy a két adatsor azonos sokaságból származik? Korábban ezt a kérdést már korábban tisztáztuk (Adatsorok szóródása – A terjedelem) és akkor arra a következtetésre jutottunk, hogy ha az adatsorok átlaga megegyezik, az önmagában még nem jelent elegendő bizonyítékot arra vonatkozóan, hogy a két adatsor azonos sokaságból származik. Azaz, ha teljesen biztosak akarunk lenni abban, hogy a két adatsor azonos sokaságból származik, akkor nemcsak azt kell vizsgálnunk, a két adatsor átlaga megegyezik, de azt is, hogy a két adatsor adatainak szóródása is megegyezik.

Ehhez természetesen szükségünk van hasonló tesztekre, mint az átlagok vizsgálata esetében, vagyis el kell tudnunk dönteni, hogy például egy vizsgált minta elemeinek szóródása megegyezik-e a vonatkozó sokaság elemeinek szóródásával, azaz lehetséges-e, hogy a vizsgálat minta az adott sokaság elemeiből lett-e kiválasztva, vagy sem. A szituáció tehát hasonló a korábban ismertetett Z-, és t-próbákhoz, de a kihívás mégis egy kicsit más, hiszen a minták szórása és varianciája nem feltétlenül viselkedik ugyanúgy, mint ahogy azt az átlagok esetében megszoktuk.

De akkor mégis hogyan viselkedik a minták varianciája a sokaság varianciájához képest? Az elméletekben való elmélyedés helyett szokásomhoz híven inkább játszanák egy kicsit a számokkal. Minitab-ban létrehoztam egy 10 000 elemből álló normál eloszlású sokaságot, amelynek az átlaga 0, a szórása pedig 1 (ez ismerős valahonnan… igen, ez az adatsor a standard normál eloszlást követi, de ez most nem lényeges). Ezt a sokaságot átmásoltam táblázatkezelőbe, és kiszámítottam a sokaság szórását és varianciáját. Ezek után készítettem 10 000 darab 6-elemű mintát, amelyeknek az elemeit véletlenszerűen választottam ki az előzőleg létrehozott sokaságból, majd mind a 10 000 mintának kiszámítottam a szórását és a varianciáját. Természetesen a 10 000 darab minta között voltak olyanok, amelyek varianciája egészen kicsi, de olyanok is, amelyek varianciája egészen nagy. A legkisebb variancia 0,02266, a legnagyobb pedig 4,373147 volt, amit találtam. Mivel a sokaság varianciája 1, ezért belátható, hogy a minták varianciája hasonlóan működik a minták átlagához, azaz a minták varianciái nem feltétlenül egyeznek a sokaság varianciájával, sőt bizonyos esetekben egészen nagy különbségek is előfordulhatnak. Igazából arra vagyok kíváncsi, hogy – hasonlóan a sokaság és a minták átlagának viszonyához – hogyan helyezkednek el a minták varianciái a sokaság varianciája körül. Ha például egy minta varianciája megegyezik a sokaság varianciájával, akkor a kettejük hányadosa (s²/σ²) 1 lesz. Ha a minta varianciája sokkal kisebb, mint a sokaságé, akkor a tört értéke kisebb, míg ellenkező esetben, amikor a minta varianciája nagyobb a sokaságénál, akkor a tört értéke nagyobb lesz, mint 1.

A kísérlet következő lépéseként kiszámítottam a fent említett s²/σ² hányadost mind a 10 000 darab minta esetében (vagyis megvizsgáltam, hogy a minták varianciái mennyire esnek messzire a sokaság varianciájától), majd ezek alapján megrajzoltam a minta varianciák gyakorisági diagramját. Íme:

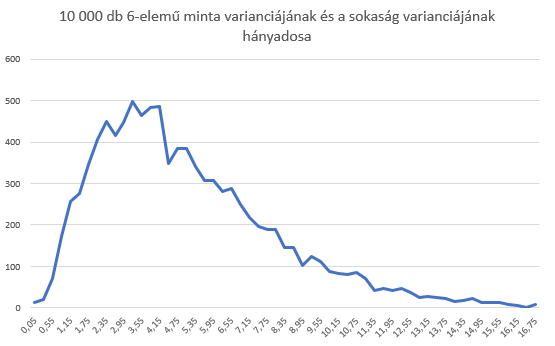
Az első dolog, ami szembetűnik a diagramon az az, hogy a minta varianciák eltérése a sokaság varianciájától semmiképp sem normál eloszlást követ, a diagram erősen balra dől és a jobboldali vége sokkal hosszabb, mint a baloldali. Viszont a görbe alakja esetleg ismerős lehet a régi kedves olvasók számára, mint ahogyan a történet is. Mintha egyszer már vizsgáltuk volna minták varianciáinak eloszlását… Igen a Khí-négyzet eloszlás ismertetésekor tárgyaltunk valami hasonló dolgot (Khí-négyzet eloszlás – Na, már megint egy újabb eloszlás!), mégpedig az volt a mondás, hogy egy standard normál eloszlású sokaságból vett minták varianciáinak eltérése a sokaság varianciáitól Khí-négyzet eloszlású!

Aha, viszont a Khí-négyzet eloszlás alakja függ a minták elemszámától, ezt jó lenne figyelembe venni a mi esetünkben is. Mi lenne, ha a fent definiált s²/σ² hányadost megszoroznánk a szabadsági fokok számával (degrees of freedom – df), azaz (n-1)-gyel? Ez a minták varianciáinak gyakoriságán nem változtatna lényegesen, viszont így elérnénk, hogy a próba statisztika eredménye Khí-négyzet eloszlású legyen, amelynek az alakja ugye függ a szabadsági fokok számától, azaz végső soron a mintaszámtól.

A fentiek igazolására elkészítettem a 2, 3, 4, 5 és 6 elemű minták varianciáinak a gyakorisági grafikonját úgy, hogy a hányadosokat megszoroztam a szabadsági fokok számával, amely így néz ki:

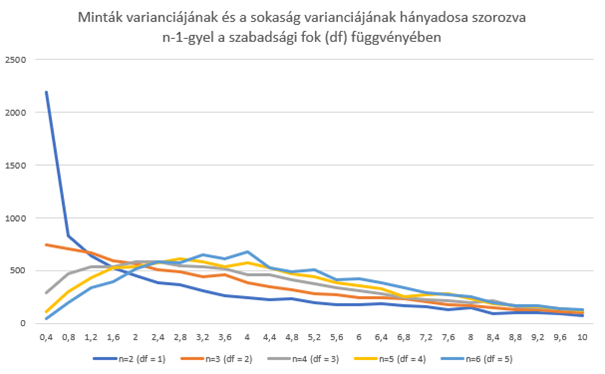
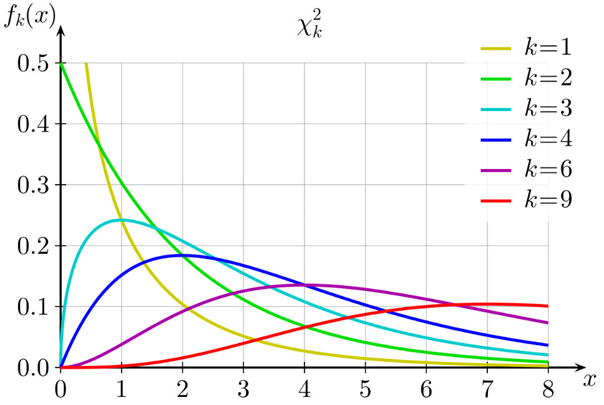
Nem lett túl szép, de összehasonlítva a wikipédián a khí-négyzet eloszlás grafikonjával, felfedezhető a hasonlóság:

A fentiek alapján tehát a minta varianciáját vizsgáló hipotézis vizsgálat próba statisztikája a következő:

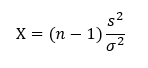
ahol

X – a hipotézis vizsgálat próba statisztikája

n – a minták elemszáma

s² - a minta varianciája

σ² - a sokaság varianciája.

Szóval akkor miről is szól ez a teszt? Az alaphelyzet az, hogy van egy sokaság, amelynek ismerjük a varianciáját és van egy n-elemű minta, amiről el szeretnénk dönteni, hogy ebből a sokaságból származik vagy sem. A nullhipotézis (H0) tehát az, hogy a minta és a sokaság varianciája megegyezik. Az ellenhipotézis pedig természetesen az, hogy a minta varianciája NEM egyezik meg a sokaság varianciájával. Értelemszerűen a potenciális következtetések pedig úgy néznek ki, hogy ha a minta és a sokaság varianciája megegyezik, akkor van annak valamekkora valószínűsége, hogy a minta elemei a sokaságból származnak, míg ha a nullhipotézist elvetjük és az ellenhipotézist fogadjuk el, akkor viszont 95%-os (vagy 99%-os) valószínűséggel kijelenthetjük, hogy a minta elemei nem a sokaságból származnak!

Egészen természetes, hogy a korábbi tesztekhez hasonlóan ez esetben is végezhetünk egyoldali vagy kétoldali hipotézis vizsgálatot is.

A teszt menete az, hogy először megvizsgáljuk a teszt előfeltételeinek teljesülését, azaz, hogy a sokaság és a minta normál eloszlást követnek-e, majd kiszámítjuk a próba statisztikát a már fentebb ismertetett képlet segítségével, majd összehasonlítjuk az adott mintaszámhoz tartozó – a teszt elején meghatározott 95%-os vagy 99%-os megbízhatósági szintű – khí-négyzet határértékkel. Ha a próba statisztika értéke nagyobb, mint a kikeresett khí-négyzet határérték, akkor a nullhipotézist elvetjük, ha pedig kisebb, akkor elfogadjuk.

A következő bejegyzésben be fogom mutatni a teszt alkalmazását táblázatkezelő program és a Minitab segítségével is.