Kijelenthetjük-e egy minta átlagának vizsgálata (Amikor túl kevés a vizsgálandó minta…) alapján, hogy a mintát valóban a kérdéses sokaságból vettük ki?

Mi a helyzet a következő esetben? Adott egy sokaság, amelynek az átlaga 0, a szórása pedig 0,3. Ez nagyjából azt jelenti, hogy a sokaság elemei nagyjából -1 és +1 között szóródnak. Van egy mintánk, amely a következő 15 elemből áll:

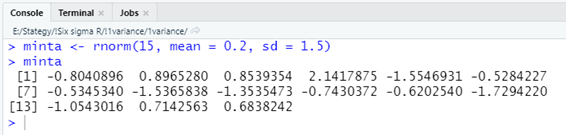
Ha egymintás t-próba alkalmazásával megvizsgáljuk, hogy ezt a mintát kivehettük-e ebből a sokaságból, akkor a következőt kapjuk:

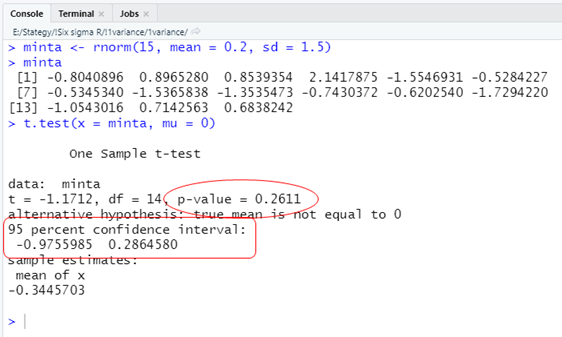
Az egymintás t-próba eredménye azt mutatja, hogy

• a p-érték nagyobb, mint 0,05,
• a 95%-os megbízhatósági intervallum alsó határa kisebb, a felső határa pedig nagyobb, mint 0, tehát nem zárható ki, hogy a sokaság és a minta átlaga megegyezik,

vagyis egyértelműen azt mutatja, hogy ezt a mintát kivehettük ebből a sokaságból.

A minta elemeit egy kicsit jobban megvizsgálva viszont azt látjuk, hogy van jó néhány olyan eleme ennek a mintának, amely mégiscsak kétségessé teszi azt, hogy ezt a mintát pont ebből a sokaságból vettem ki.

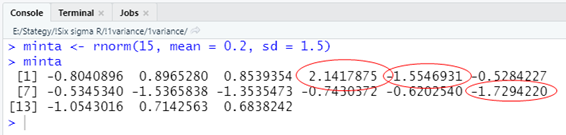
Ha a sokaság elemeinek 99,9%-a -0,927 és + 0,927 között van, akkor hogyan vehettünk ki ebből a sokaságból egy olyan mintát, amelyben van 2,14, -1,72 vagy -1,55?

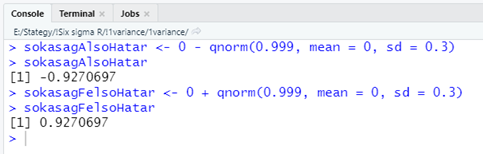
Vajon mekkora a valószínűsége, hogy a sokaságunknak van olyan eleme, amely nagyobb, mint 2,14 vagy kisebb, mint -1,72 vagy netalán -1,55? (feltételezve, hogy a sokaság normál eloszlású)

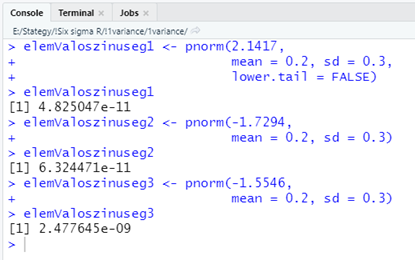
Egy kicsivel látványosabb, ha egy diagramon is megmutatom a sokaság és a minta viszonyát (Az R-kódot a cikk végén található linkről le tudod tölteni).

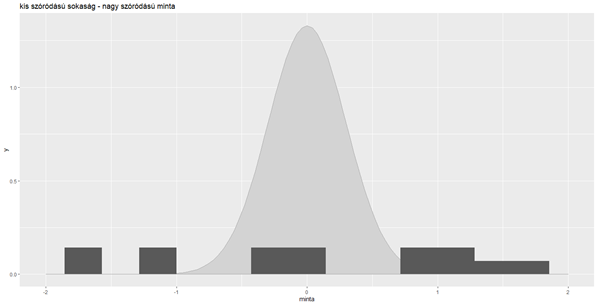
Amint az látható, ezeknek az elemeknek az előfordulási valószínűsége a sokaságban igencsak elenyésző. Akkor most mennyire vehetem komolyan a t-próba eredményét? Ha esetleg hosszabb ideje olvasod a blogot, már találkozhattál ezzel a probléma felvetéssel (Ja, hogy szóródás is van a világon…! – Khí-négyzet teszt a variancia vizsgálatára (1-variance)), csak talán nem ennyire konkrétan megfogalmazva.

Szerencsére a fent említett blogbejegyzés bemutatja a módszert, amellyel össze tudjuk hasonlítani a minta és a sokaság varianciáját és egy másik bejegyzésben (Hogyan csináld Minitab-bal? - Khí-négyzet teszt a variancia vizsgálatára (1-variance)) már azt is bemutattam, hogy lehet egy ilyen vizsgálatot elkészíteni a Minitab program segítségével. Most viszont az a cél, hogy ugyanezt R-ben is elvégezzük.

Érdekes módon az R alapcsomagjában található ’var.test()’ függvény nem képes a fenti teszt elvégzésére, csak két minta varianciáját tudja összehasonlítani (F-teszt). Az ilyen típusú egymintás khí-négyzet teszt elvégzéséhez egy már korábban megismert csomagban találunk megoldást. Ez az ’EnvStats’ csomag, amelyről már korábban leírtam, hogy kifejezetten környezeti statisztikák elkészítésére fejlesztették ki. Ebben a csomagban található a ’varTest()’ függvény – amely neveik hasonlósága ellenére nem tévesztendő össze a fentebb említett ’var.test()’ függvénnyel – amelynek az alkalmazásával el tudunk készíteni egy ilyen vizsgálatot. A különféle R irodalmak ezt a tesztet egyébként „One-sample chi-square test for variance”-ként vagy „Single Variance Chi-Square Test”-ként, illetve ehhez hasonló elnevezésekkel hivatkozzák meg. A függvény bemutatásához a fenti példát szeretném felhasználni.

 A ’varTest()’ függvénynek szerencsére nincs sok paramétere, amit meg kellene / lehetne adni.

• Az ’x =’ paraméter a vizsgált minta adatsor,
• A ’sigma.squared =’ paraméter a sokaság elméleti varianciája (szerintem direkt lett „szigmanégyzet” a neve, nehogy a szórást írja be valaki). Ez esetben a sokaság elméleti szórása 0,3, amelynek a négyzete 0,09.
• A ’conf.level =’ argumentummal lehet megadni, hogy milyen megbízhatósági szinten szeretnénk teszten (0,95 = 95%, 0,99 = 99%, stb.)
• Az ’alternative =’ paraméterrel pedig azt tudjuk megadni, hogy kétoldali vagy egyoldali tesztet szeretnénk végrehajtani („two.sided” = kétoldali, „greater” = jobboldali, „less” = baloldali teszt - Igaz vagy hamis? – A hipotézis vizsgálatokról…)

A teszt eredménye elsőre kissé kuszának tűnhet, de a felépítése egészen hasonló az egymintás t-próbához.

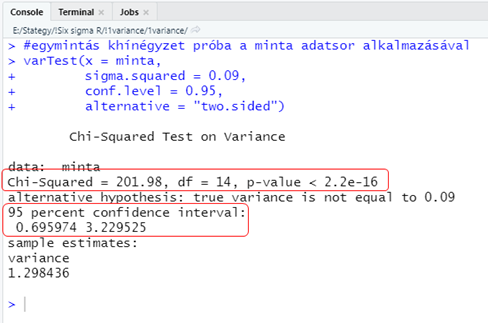
A Chi-Squared = 201.98’ a teszt próbastatisztikája, ’df = 14’ jelentése csak annyi, hogy milyen szabadsági fokú khí-négyzet eloszlást használt a teszt a khí-négyzet határérték meghatározásához, a ’p-value = 2.2e-16’ jelentése pedig az, hogy 2,2 * 10^-16 az esélye annak, hogy a mintát egy olyan sokaságból vettük ki, amelynek a varianciája 0,09. Mivel ez egy igen kicsi szám, de mindenképpen kisebb, mint 0,05, kijelenthetjük, hogy a nullhipotézist elutasítjuk és elfogadjuk az ellenhipotézist, hogy ezt a mintát nem vehettük ki ebből a sokaságból.

Összegzés:

Szeretném kiemelni a fontosságát annak, hogy amikor azt vizsgáljuk, hogy egy mintát kivehettünk-e egy adott sokaságból, akkor nem elegendő a minta átlagának vizsgálata, mindenképpen meg kell vizsgálnunk a minta és a sokaság szórásának viszonyát is. Érdemes lehet még megvizsgálni, hogy vannak-e a mintában kieső értékek (Kancsal tengerész nem tud célozni! – Kieső értékek vizsgálata), de erről majd egy másik bejegyzésben még szó esik majd.

A bejegyzésben használt R kódokat innen tudod letölteni.

Források:

varTest function – R documentation
https://www.rdocumentation.org/packages/EnvStats/versions/2.3.1/topics/varTest