
A múlt heti bejegyzésben (A mintaátlagok tánca) megértettük, hogy egy adott sokaságból kivett minták tulajdonságai nem feltétlenül adják vissza a sokaság tulajdonságait, van ebben nem kevés bizonytalanság. Sajnos azonban ez nem változtatott azon az alaphelyzeten, hogy a mintát ismerjük, a sokaságot pedig nem. Pechünkre a hegy nem fog eljönni Mohamedhez, így szegény Mohamednek sem lesz más választása, mint elballagni a hegyhez. Ez azonban nem tűnik egyszerűnek...
Mielőtt belevágunk a történetünk folytatásába, ismét arra bátorítalak, kedves olvasó, hogy egy másik lapon nyisd meg a már korábban hivatkozott weboldalt, ahol a szimuláció található és játssz el a beállításokkal, készíts sok-sok mintát és próbáld ki mindazokat a dolgokat, amelyeket a továbbiakban megpróbálok elmagyarázni neked.
https://www.esci.thenewstatistics.com/esci-dances.html
Nos, a kiindulási pontunk ugyanaz, mint az előző cikkben. Van egy mintánk, amiről feltételezzük, hogy egy bizonyos sokaságból vettük ki.

A fenti ábrán lévő μ viszont csak egy feltételezés, nem vagyunk benne biztosak, hogy a sokaság átlaga valóban ennyi. Akkor viszont marad a nagy kérdés, hogy akkor vajon hogyan tudunk meggyőződni arról, hogy ezt a mintát valóban pont egy ilyen sokaságból vettük ki.
Mivel a sokaság átlagát nem ismerjük, így jobb híján a minta átlaga alapján próbáljuk meg megbecsülni azt a tartományt, ahol a sokaság átlaga lehet! Hoppá, ez pont a fordítottja annak a gondolatmenetnek, amit eddig alkalmaztunk. Az előző cikkben sok mintát vettünk a sokaságból és azt láttuk, hogy a mintaátlagok jelentős része egy megadott tartományba esik. Most ezt a tartományt a minta átlagából becsüljük meg, és azt nézzük, hogy a sokaság feltételezett átlaga beleesik-e a mintaátlag alapján becsült tartományba:

Amennyiben ismernénk a feltételezett sokaság szórását is, úgy annak a felhasználásával tudjuk megbecsülni ezt a bizonyos tartományt, ha viszont nem, akkor sajnos nem marad más, csak a minta szórása. Ez persze további bizonytalanságot visz be a rendszerbe, mivel főleg kis elemszámú minták esetében jelentős eltérés lehet a sokaság és a minta szórása között. Ez nem feltétlenül igaz, de sohasem tudjuk, hogy ez a különbség mekkora. Sajnos a saját gyakorlatomban még kevés olyan feladattal találkoztam, amikor ismertem a sokaság szórását...
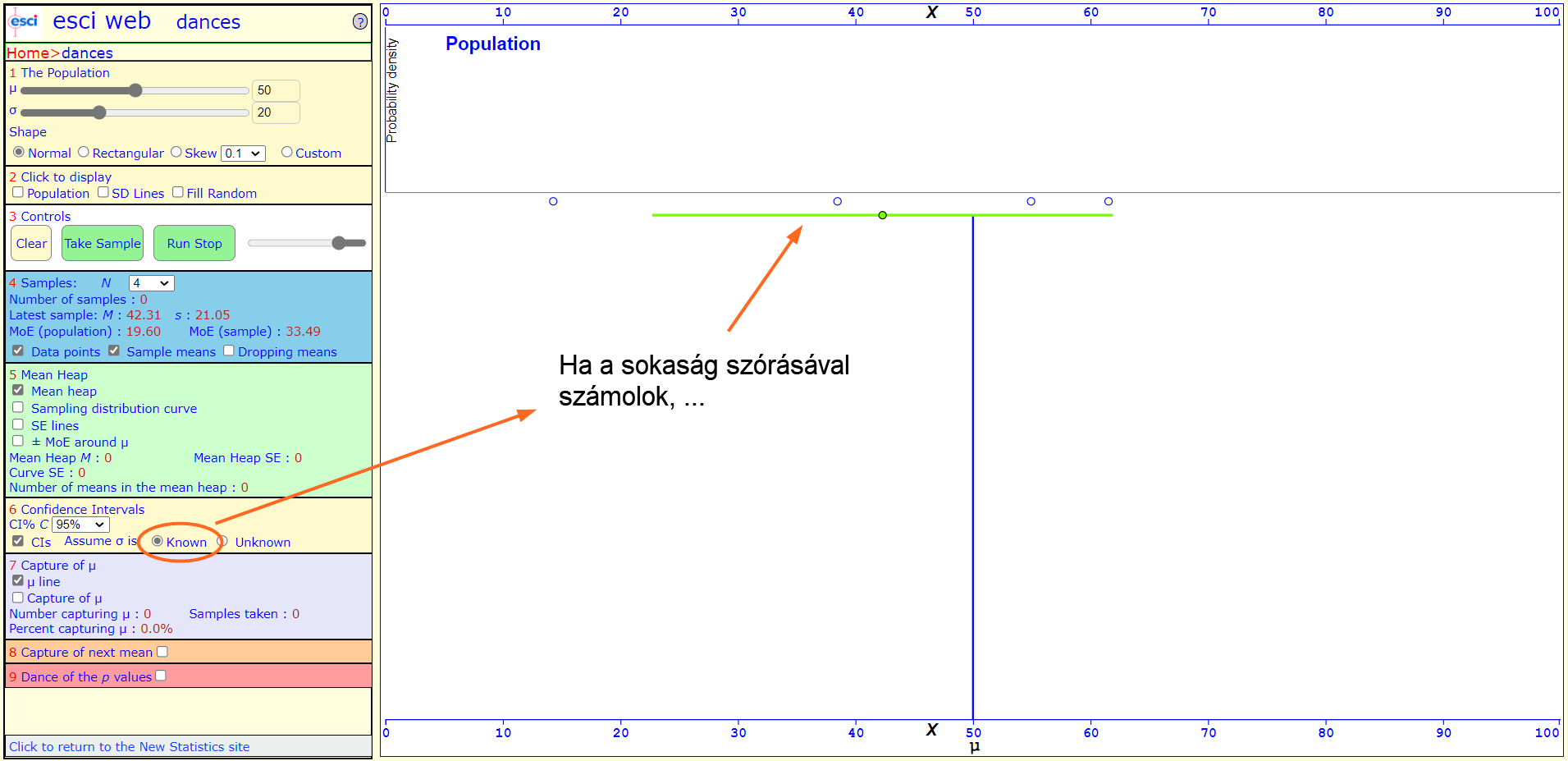
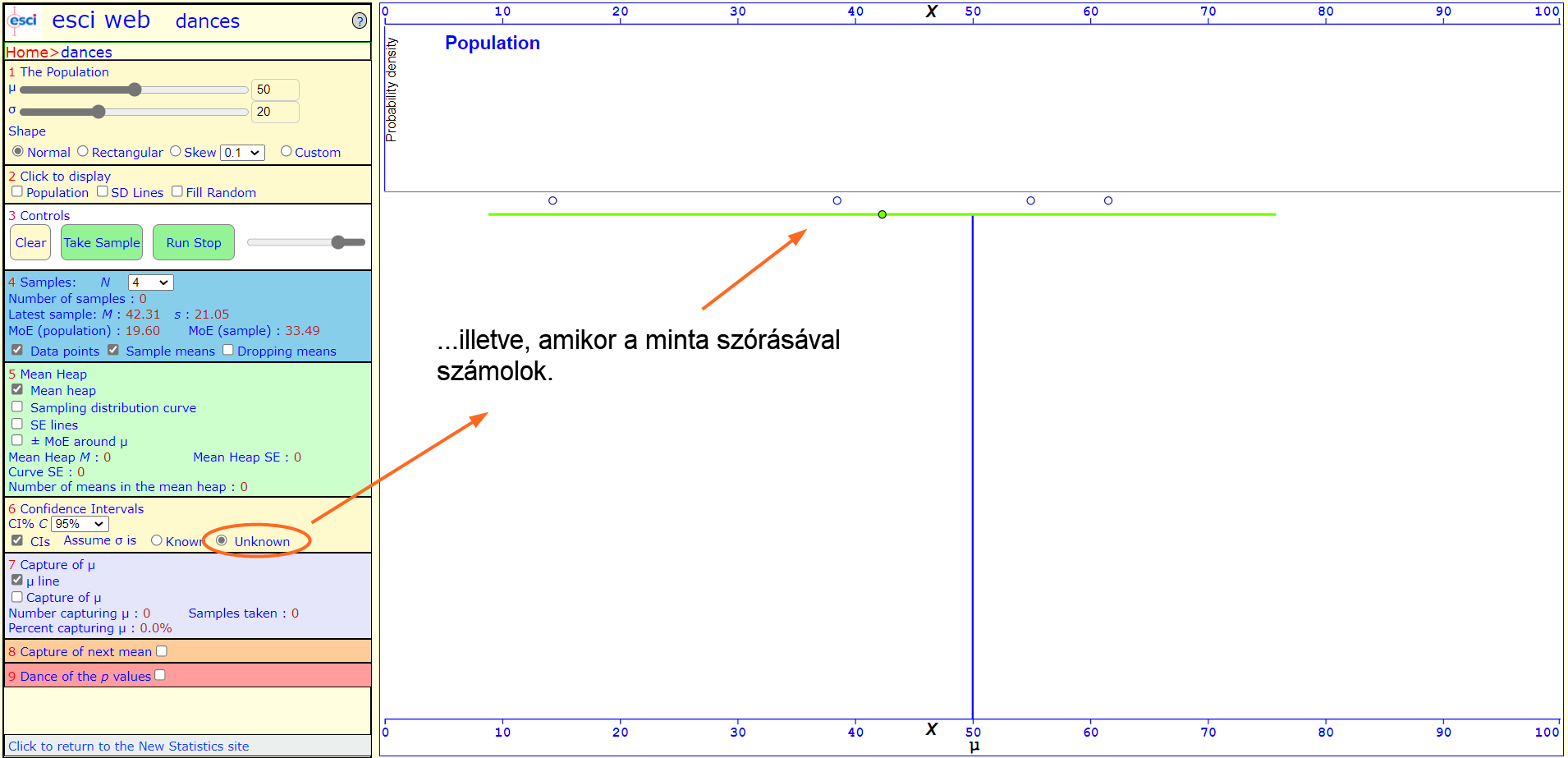
És hogyan határozzuk meg ezt a tartományt? A nagy dobókocka kísérletben (A nagy dobókocka kísérlet) azt tapasztaltuk, hogy a mintaátlagok szórása megegyezik a sokaság szórásának és a minták elemszámának hányadosával:
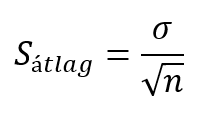
Vagyis csak annyit kellene tennem, hogy a minta átlagához átlagához hozzáadom, illetve abból kivonom a mintaátlagok szórásának kb. kétszeresét (normál eloszlás esetében a ± kétszeres szórástartományban van benne az elemek 95%-a), és akkor meg is kapom azt a tartományt, ahol a mintám átlaga mozoghat abban az esetben, ha azt a feltételezett sokaságból vettem ki.

Tehát, amennyiben a feltételezett sokaság átlaga beleesik ebbe a minta által megadott tartományba, akkor nem jelenthetjük ki azt, hogy a mintát nem ebből a sokaságból vettük ki. Próbáljuk ki ezt sok-sok mintával is:
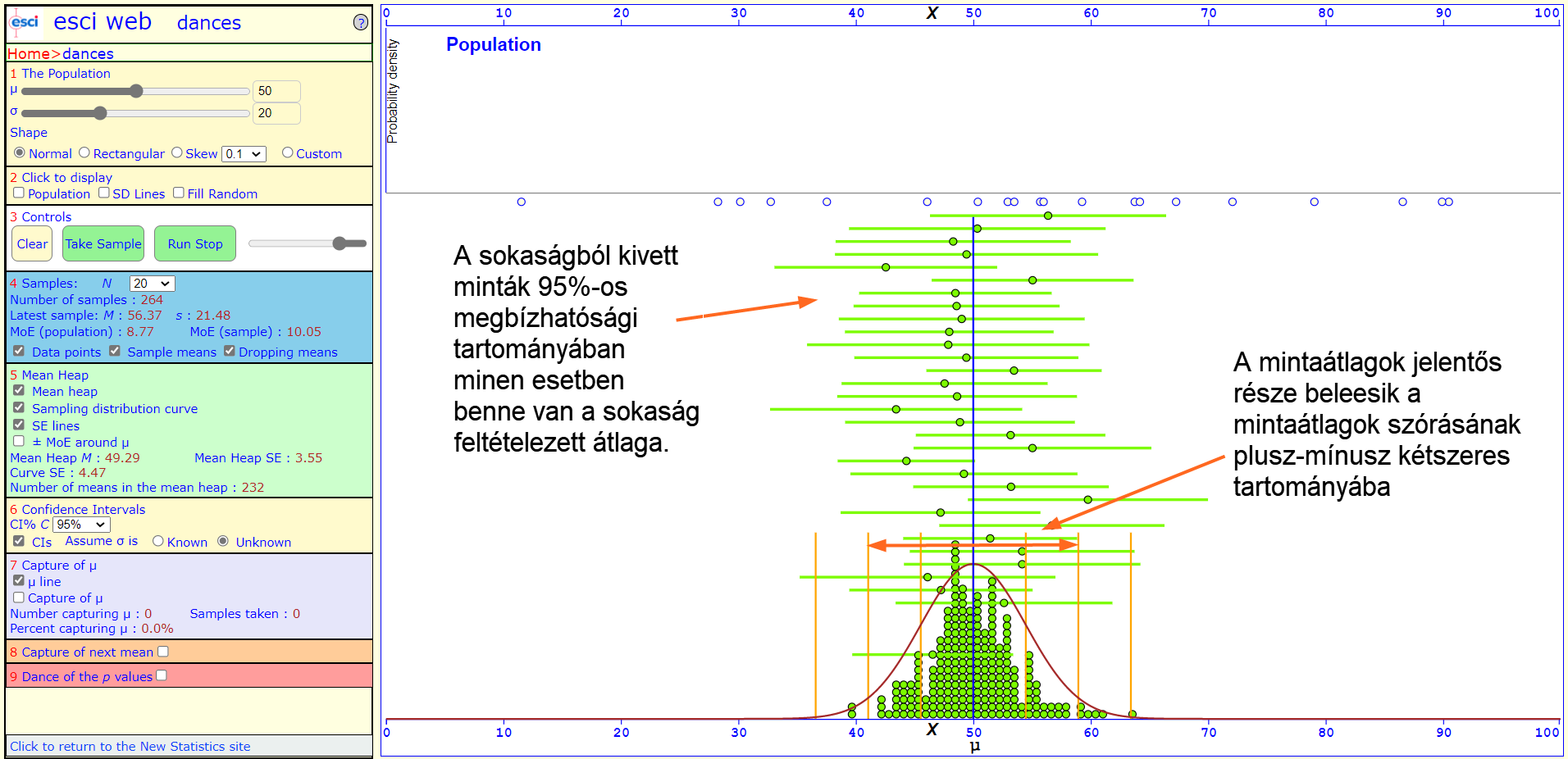
A fenti példa azt mutatja be, amikor ugyanabból a sokaságból veszünk ki sok-sok mintát, akkor kb. 95%-os valószínűséggel - azaz 100 esetből kb. 95-ször - a sokaság feltételezett átlaga benne lesz a minta tulajdonságaiból számolt megbízhatósági intervallumban. De nem minden esetben!

Ahogy azt a fenti ábra mutatja, ritkán azért előfordul olyan eset is, amikor a sokaság feltételezett átlaga mégsincs benne a minta megbízhatósági tartományában ANNAK ELLENÉRE, hogy a mintát a sokaságból vettük ki. Ilyenkor sajnos hibás döntést hozunk. De tulajdonképpen nem is mondta senki, hogy a döntésünk minden esetben jó lesz, csak azt, hogy 95%-os megbízhatósággal lesz jó!
Azzal, hogy milyen szigorúan fogjuk megadni az α értékét, mi magunk döntjük el, hogy mennyire akarunk biztosak lenni abban, hogy helyesen döntünk (Számítógépes bowlingozás egymintás Z-próbával).
Az az érdekünk persze, hogy minél biztosabbak legyünk a döntésünkben. De ha megnöveljük α értékét 95%-tól mondjuk 99%-ra, azzal lecsökkentjük a hiba valószínűségét, azonban megnöveljük a minták tulajdonságaiból számolt megbízhatósági tartomány szélességét, azaz növeljük a teszt bizonytalanságát!
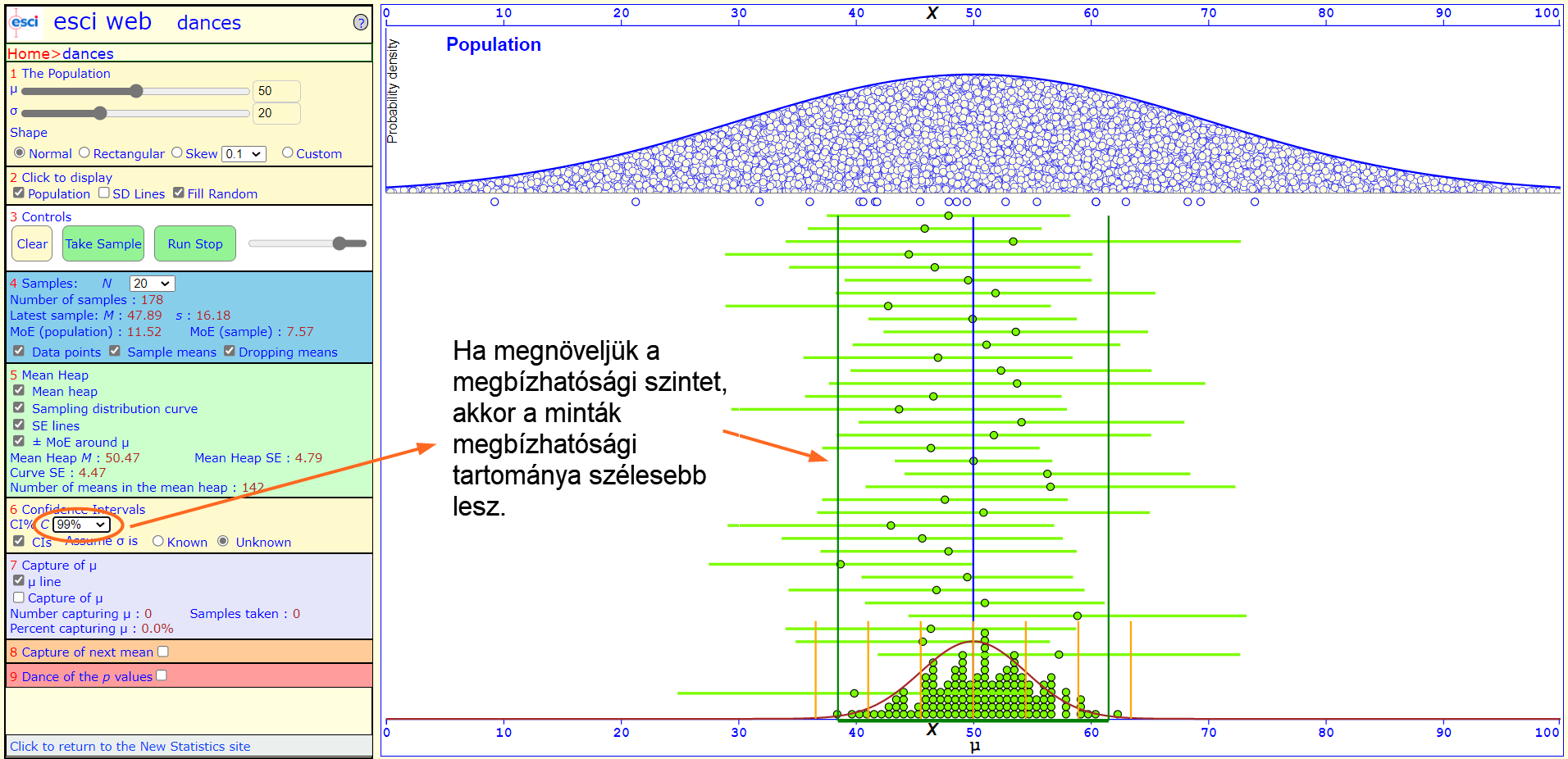
Hogyan lehet akkor nagyobb megbízhatósági szint mellett mégis szűkíteni a minták megbízhatósági tartományát? Úgy, ha megnöveljük a minták elemszámát!
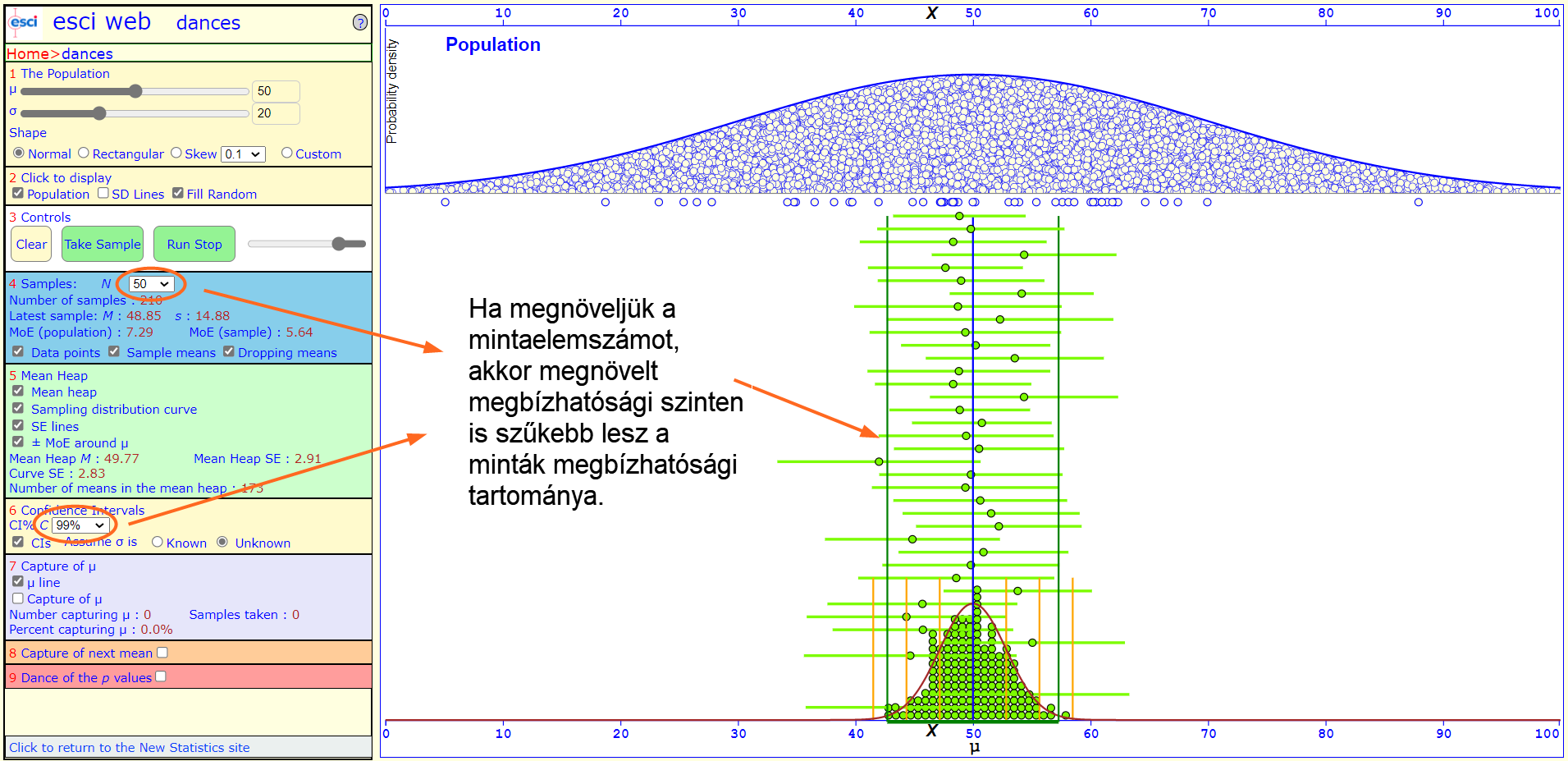
A minták elemszámának növelése azonban sajnos egyéb financiális, időbeni és akár morális kérdéseket is felvethet, így sajnos nem tudjuk elérni a tökéletességet, csak elfogadható kompromisszumokat tudunk kötni. Van, hogy inkább felvállaljuk a hibázás minimális lehetőségét a gyors és olcsó eredmény elérése érdekében, máskor inkább több időt és pénzt áldozunk a kísérletünkre annak érdekében, hogy a döntésünk helyesebb legyen.
Összefoglalás:
Amikor egy kísérletet végzünk, akkor egy mintát veszünk ki a sokaságból, magáról a sokaságról nagyon keveset tudunk, maximum feltételezéseink vannak róla. Nem marad más hátra, minthogy a minta tulajdonságaiból próbáljunk meg következtetéseket levonni a sokaság tulajdonságaival kapcsolatban. Ahhoz azonban, hogy helyes döntést tudjunk hozni, ismernünk kell és el kell fogadnunk a sokaság és a minta kapcsolatának törvényszerűségeit. Nincs tökéletes döntésre lehetőségünk, a hiba valószínűsége mindig benne van a rendszerben, de a megbízhatósági szint helyes megválasztásával kiszámíthatóvá tudjuk tenni a döntésünk kockázatait. A minta elemszámának növelésével javítani tudjuk a becsléseink minőségét, de ezt sokszor behatárolják az időbeni, anyagi és egyéb lehetőségeink.
Források:
Geoff Cumming & Robert Calin-Jageman: Introduction to the new statistics: Estimation, Open Science, and Beyond, Routledge Subs. of International Thomson Org. 29 West 35th Sreet New York, NYUnited States, October 2016
ISBN:978-1-138-82552-9
Geoff Cumming youtube-csatornája
https://www.youtube.com/channel/UCwRbwVb6mRKuyXtV1td-vig





