Nem biztos, hogy mindenki így tanulta a kombinatorikát, de amikor először megláttam ezt a fajta levezetést, akkor rögtön beugrott, hogy én ezt így már hallottam valamikor az általános iskolában vagy a gimnáziumban. Én mindig is kevertem a permutációt, a kombinációt és a variációt szóval nem árt, ha tisztázzuk valamilyen egyszerű és játékos módszerrel, hogy melyik mi is valójában.

A statisztika alkalmazását jelentősen megkönnyítik a különböző szoftverek és alkalmazások, mert használatukkal a bonyolultnak tűnő számítások is játszi könnyedséggel végezhetők el. Beadjuk az adatokat a szoftvernek, amely kidobja az eredményt. Akkor mégis miért kell megérteni és megtanulni azt a rengeteg elméletet és képletet, amely ebben a könyvben szerepel? Miért nem elég csak beadni az adatokat, megnyomni a gombot és megkapni a végeredményt?

Az egyik előző bejegyzésben (lásd itt) már távolról pedzegettem a témát, hogy jó lenne tudni valamit arról, hogy az adataink milyen eloszlást követnek. A számítógép előtti időkben igen időigényes volt az adatok ábrázolása vagy bonyolultabb számítások elvégzése az adatsorokon. Az igény mégis megvolt arra, hogy valamilyen egyszerű módon következtetni lehessen az adatsor eloszlására vagy legalábbis arra, hogy az adatsor normál eloszlást követ-e vagy sem. Szerencsére a normál eloszlásnak van egy-két olyan tulajdonsága, amelyek segítenek abban, hogy néhány egyszerű számítás alapján legyen egyáltalán ötletünk arról, hogy az adatsorunk normál eloszlású-e vagy sem.

(A videó a képre kattintva indul el)

Az átlag standard hibája (Standard Error of the Mean) egy kicsit nehezebben emészthető fogalom, de tárgyalását két okból sem tudjuk megúszni:

1. Minden híreszteléssel és hiedelemmel ellentétben a sokaság átlaga SOHASEM egyezik meg a minta átlagával, a mintaátlag alapján csak becsülni tudjuk, hogy a sokaság átlaga vajon mekkora lehet. 

2. A leíró statisztikákban igen gyakran megjelenik, ezért jó, ha tudjuk mit jelent az az "se" vagy "SE Mean", amitvel olyan gyakran találkozunk ezekben a riportokban.

Remélem emészthető lesz a magyarázat.

Jó szórakozást!

Korábbi statisztikai tanulmányaim során mindig azt tanultam, hogy ha egy folyamatot csak véletlenszerű tényezők befolyásolnak, akkor az adott folyamat eredménye normál eloszlást követ. Ezen gondolkodva jutott eszembe az ötlet, hogy mi lenne, ha valamilyen természeti jelenségen próbálnám ki, hogy vajon tényleg mindenre működik-e a fenti elmélet. És ekkor eszembe jutott, hogy van a polcon egy kosárnyi szárított sárgabarack mag: mi lenne, ha megmérném ezeknek a tömegét és kielemezném, hogy a barackmagok tömegének eloszlása milyen.

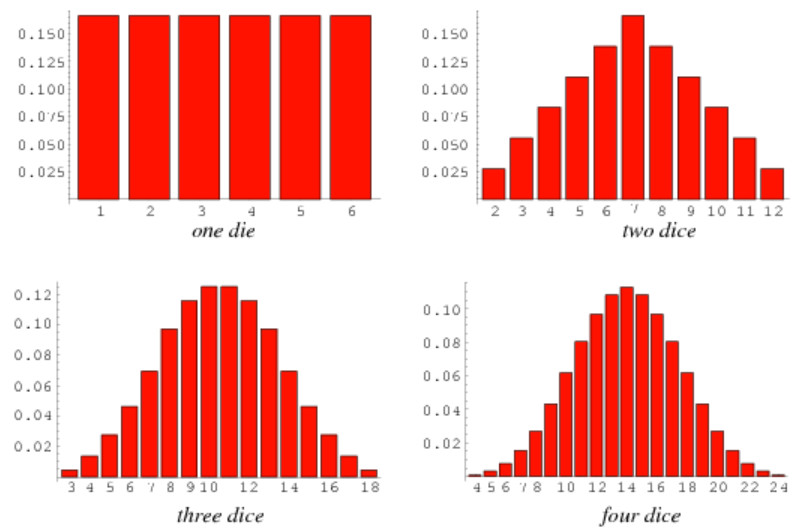Hosszú út vezetett a normál eloszlás pontos leírásáig a szerencsejátékoktól kezdve a csillagászaton át a skót katonák mellbőségének elemzéséig. 1654 óta sok híres matematikus gondolkodott erről a természetben igen gyakran tapasztalható jelenségről. A normál eloszlás először nem is normál eloszlásként volt ismert, Galilei fejtette ki 1632-ben, hogy a bolygók helyzetének meghatározásakor kisebb-nagyobb hibákat lehet megfigyelni, amely visszavezethető a megfigyelő, a megfigyeléshez használt eszközök és a megfigyelés körülményeinek bizonytalanságaira. Ezek a hibák szimmetrikusan helyezkednek el a bolygó valós pozíciója körül, kisebb hibák gyakrabban, nagyobb hibák ritkábban fordulnak elő. Sajnos azt a kérdést már nem tette fel, hogy ezeket a hibákat hogyan lehetne megbecsülni. Tehát először a mérendő jellemzők átlag körüli szóródását inkább észlelési hibaként kezelték és nem természetes jelenségként. Ez a felfogás még nagyon sokáig így is maradt. De akkor honnan jön a normál eloszlás elnevezése?

Tibor az elmúlt másfél évben egy műanyag házakat fröccsöntő üzem termelési vezetője volt. Ebben az időszakban Tibor kiemelten foglalkozott azzal, hogy megértesse beosztottaival, mennyire fontos a vevői követelményeknek való megfelelés. Még egy szigorú termékellenőrzési programot is bevezetett, amelyet „A Vevő hangja” néven nevezett el. A program eredményei nagy jók voltak. A részlegen vezetett feljegyzések alapján az látszott, hogy az elmúlt 9 hónapban csak olyan termék került kiszállításra a vevőkhöz, amelyek mindenben megfeleltek a vevői követelményeknek. Ez alatt az idő alatt semmilyen vevői reklamáció sem érkezett a műanyag házakkal kapcsolatban.

Ennek ellenére a múlt hónapban a vevők elkezdtek reklamálni, hogy törnek a műanyag házak. Tibor elhatározta, hogy a végére jár az ügynek.

A vizuális ellenőrök munkáját talán nem kell bemutatnom senkinek, hiszen ez egyre inkább hozzátartozik egy termelő vállalat életéhez. A vizuális ellenőrök feladata folyamatosan ellenőrizni a termékeket, amelyek leesnek a gyártósor végén és meg kell találniuk sokszor a legapróbb és legnehezebben észrevehető hibákat is. Persze ne feledkezzünk meg azokról a vizuális ellenőrökről sem, akik például egy repülőgép különféle alkatrészeit vizsgálják és az elhasználódást jelző apró repedéseket próbálják felderíteni.

(A képre kattintva megnyílik az előző bejegyzés)

A német tank problémáról szóló bejegyzés után az olvasók egy része hitetlenkedett, véleményük szerint a leírt módszer megbízhatatlan. Mivel ez a kritika sokszor elhangzott, ezért engem is elkezdett foglakoztatni a kérdés, hogy hogyan lehetne igazolni a módszer megbízhatóságát. Először arra gondoltam, hogy ismét készítek egy csomó minta adatsort és ezeken tesztelek, de aztán egyszer csak jött az ötlet, hogy tulajdonképpen van egy szabadon hozzáférhető hatalmas adathalmaz, amelynek létrehozásakor egymás után szépen sorbarendezett számok halmazából választanak ki véletlenszerűen öt vagy hat számot. Igen, a lottószámok!

Mindkét adatsor átlaga 20, de az első adatsor elemeinek szóródása sokkal kisebb, mint a második adatsoré.

adatsor 1	adatsor 2