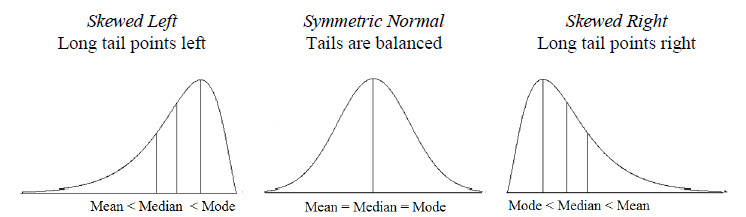
A középérték mérőszámok esetében már volt szó a mediánról, amely az adatsor középső eleme, vagy a két középső elem átlaga. Ezzel az erővel tovább is szeletelhetjük az adatsorunkat, mondjuk négyfelé, ötfelé vagy akár tízfelé.

A Bernoulli eloszlás Jacob Bernoulli svájci matematikusról kapta a nevét, aki kitalálta a Bernoulli próbát, amely a világ egyik legegyszerűbb valószínűségszámítási kísérlete. Tegyük fel, hogy feldobunk egy darab érmét egy alkalommal. Az érme feldobásának, mint eseménynek kétféle végeredménye lehet. Nevezzük el a kétféle végeredményt k-val, és ha az érme úgy érkezik, hogy a fej van felfelé, akkor ezt nevezzük el sikernek és jelöljük k = 1-gyel, ha pedig az érme az írás oldalával felfelé esik le, akkor ezt értelmezzük kudarcként és jelöljük k = 0-val.

J

Végre megérkezett a második videó, amelyből végre kiderül, hogy miért kell n-1-gyel osztani a variancia és a szórás képletében, ha a minta jellemzőivel számolunk.

Jó szórakozást!

 
forrás: Wikipédia

A német tank probléma a nevét egy a II. Világháború idején felmerült problémára alkalmazott megoldás után kapta. A szövetséges haderők számára nagyon fontos lett volna ismerni, hogy a németek mennyi Panzer V („Panther” azaz párduc) típusú tankot gyártottak a háború évei alatt. A szövetséges hírszerzés minden erőfeszítés ellenére sem volt képes megbízható számadatokkal szolgálni. Végül rájöttek, hogy a németek nagyon precízen egymás után következő egyedi sorszámokkal látták el a legyártott tankok sebességváltó házait. Ekkor elkezdték összegyűjteni a kilőtt vagy elfogott tankokon található sorszámokat és ezek alapján sikerült megbecsülni a legyártott tankok számát, amely lényegesen kisebb volt, mint a hírszerzési becslések. A háború végén, amikor a Szövetségesek végül hozzájutottak a németek termelési adataihoz, akkor derült ki, hogy a tankok sorszámai alapján kiszámított becslések sokkal pontosabbak voltak, mint a szövetséges hírszerzés által adott információk.

Ez az egyik legegyszerűbb eloszlás típus. Kezdjük ezzel, hiszen a kockadobások miatt már egyébként is sokat beszéltünk erről a fajta eloszlásról.

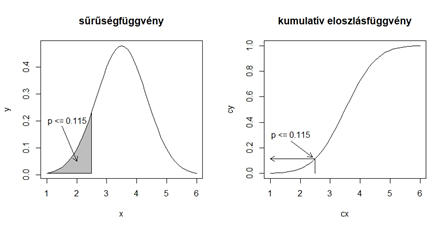Tegyük fel, hogy az általunk vizsgált eseménynek nem véges számú, hanem végtelen számú lehetséges végkimenetele van. Ez a kockadobások vizsgálatára nem igaz viszont, ha a kockadobásokat tízes csoportokba soroljuk és a tízelemű minták átlagait vizsgáljuk, akkor viszont az átlagok végtelen számú különféle értéket vehetnek fel.

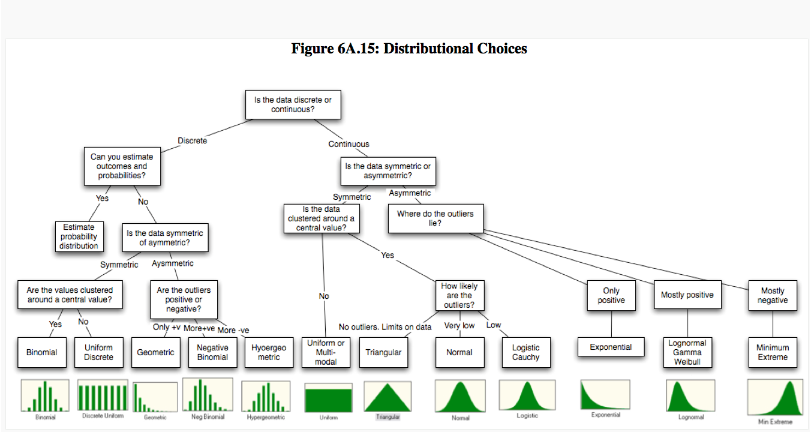A gyakorisági eloszlással kapcsolatban be kell vezetnünk a valószínűségi változó fogalmát (sajnos ezt nem tudjuk megúszni).

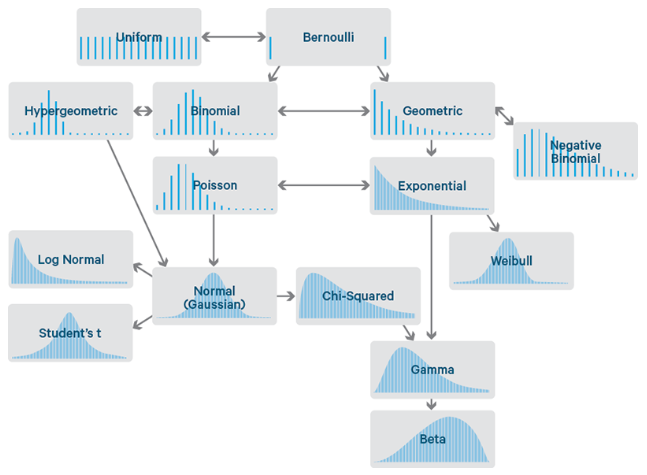
A véletlen mindenfajta szabályszerűség és szabályos mintázat hiánya, amely segítene megjósolni egy jövőbeni esemény bekövetkezését. A véletlenszerű események sorozata nem követ semmilyen mintázatot vagy szabályt, ezért a következő esemény végkimenetelét semmilyen módon nem tudjuk kitalálni.

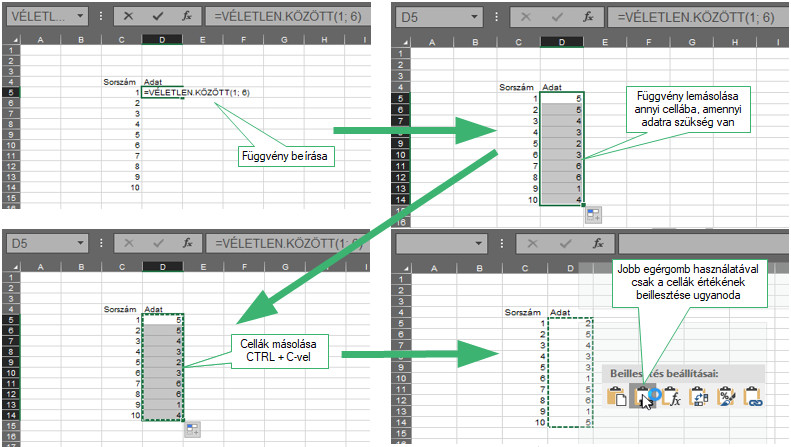
Az a véleményem, hogy a valószínűségszámítás és a statisztikai módszerek megértésében többet segít egy jó példa, mint az elméleti levezetések. Szerencsére az excel segítségével nagy mennyiségben tudunk véletlenszámokat generálni, így egy „sokaság” létrehozása nem olyan nagy gond. Legegyszerűbben a „=VÉLETLEN.KÖZÖTT()” függvény segítségével tudunk véletlenszámokat létrehozni, ezt a függvényt használtam a nagy dobókocka kísérlet során.

Amint az jól látható volt, a függvény remekül működött, az egyetlen dolog, amire oda kell figyelni, hogy a függvény által létrehozott adatsor egyenletes eloszlású! Ha másfajta eloszlású adatsort szeretnénk létrehozni, akkor még további trükközésre is szükség van.

(A videó a képre kattintva indul el)

Eddig valahogy eléggé zűrzavarosan élt a fejemben, hogy mikor és miért kell 'n' helyett 'n-mínusz-eggyel' osztani a variancia és a szórás kiszámításakor. Nem mintha ez olyan nagyon-nagyon fontos lenne, de a pontosság kedvéért azért jó, ha tisztázzuk.