Korábban már részletesen foglalkoztam több bejegyzésben is a normál eloszlással. Tisztáztuk, hogy az ugyanarról a fáról származó barackmagok tömege normál eloszlást követ (Milyen eloszlást követ a barackmag tömege?), elemeztük, hogy miért találkozhatunk a normál eloszlással annyi helyen a természetben (Miért fordul elő a normál eloszlás olyan gyakran a természetben?), megismertük a normál eloszlás legfontosabb tulajdonságait (Ismerd meg a hibafüggvényt! – A normál eloszlás legfontosabb tulajdonságai), tisztáztuk, hogy mi az a standard normál eloszlás (Első az egyenlők között – a standard normál eloszlás), sőt még valószínűséget is számoltunk normál eloszlású adatsor esetében (Esemény valószínűségének kiszámítása normál eloszlású sokaság esetén).

Ezzel együtt eddig nem tisztáztuk, hogy mégis miért olyan fontos a számunkra, hogy az adatok normál eloszlásúak legyenek. Sajnos ezt korábban nem emeltem ki megfelelő mértékben, de a korábban már ismertetett hipotézis vizsgálatok jelentős részében az az előfeltevés, hogy az adathalmaz, amelyből kivett mintákat vizsgálunk, normál eloszlású. Ez igaz az alkalmazott képletekre, a megbízhatósági intervallumok kiszámítására, illetve a teszt döntést segítő p-value (A titokzatos P színre lép – Mi az a P-Value?) értékének meghatározásakor is. A nem normál eloszlású adatok vizsgálata olyan eszközökkel, amelyek az adatok normál eloszlását feltételezik, természetesen azt eredményezik, hogy a hipotézis vizsgálatkor rossz döntést hozhatunk.

Nézzük meg ezt egy példán keresztül:

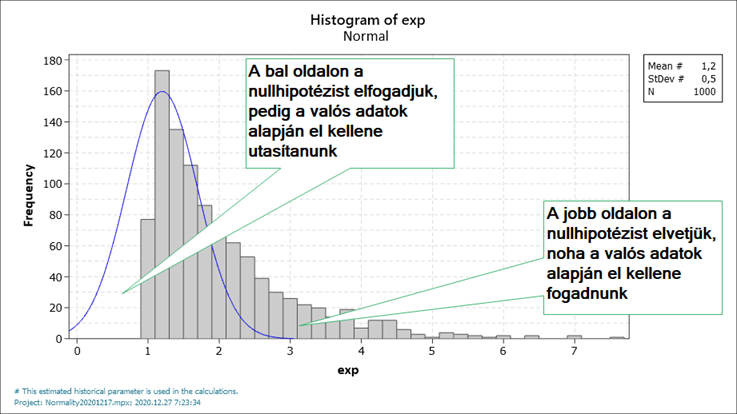
A példában nagy mennyiségű exponenciális eloszlás szerinti adatot generáltam, hogy jól látszódjon az adatok eloszlása. Az exponenciális eloszlást azért választottam, mert erősen aszimmetrikus eloszlásról van szó, így a fenti diagram kiválóan szemlélteti, hogy milyen hibákat követhetünk el, ha például egy ilyen aszimmetrikus eloszláson próbáljuk meg a normál eloszlás alapján meghatározott törvényszerűségeket alkalmazni. Az elvégzett hipotézis vizsgálat eredményeként a bal oldalon a nullhipotézist elfogadjuk, noha a konkrét adatsor alapján már el kellene utasítanunk, a jobb oldalon viszont elutasítjuk a nullhipotézist, pedig az adatok alapján el kellene fogadnunk.

Ezért aztán a Six Sigma módszertanban (is) erősen ajánlott az adatok eloszlásának vizsgálata mielőtt bármilyen statisztikai vizsgálatba belekezdenénk. Az adatok eloszlásának vizsgálata természetesen jó ideje foglalkoztatja az ezzel foglalkozó tudósokat, akik jó néhány módszert ki is dolgoztak erre a célra. A normalitás vizsgálatának természetesen megvan a maga fejlődéstörténete, az alkalmazható módszerek között vannak jól és kevésbé használhatóak is, mindegyiknek megvan a maga előnye és hátránya. Nekem eddig mindig problémát okozott, hogy mikor melyiket alkalmazzam. A továbbiakban megpróbálom – relatíve röviden – bemutatni a leggyakrabban alkalmazott eszközöket.

Vizuális eszközök.

Mivel az adatsorok eloszlását nagyon sok esetben úgy jellemezzük, hogy adott intervallumban az adatok mekkora hányada fordul elő, ezért az egyik legegyszerűbb módszer az adatok eloszlásának vizsgálatára, ha hisztogramot készítünk az adatokból (Hisztogram - amiről már sok szó esett korábban...). A hisztogram elkészítése egyszerű és gyors, hátránya viszont, hogy kevés adat esetén, vagy ha az x tengelyen az intervallumokat nem jól választjuk meg, akkor az eredmény nem igazán értelmezhető. Ráadásul a hisztogram nem ad nekünk egyértelmű döntési kritériumot arról, hogy az adatok normál eloszlásúak-e vagy sem.

Ha kevés adatunk van, akkor érdemes kipróbálni egy másik fajta ábrázolási módot, az úgynevezett Q-Q plot-ot. A neve a quantilisekből jön, igazából hívhatnánk quantilis-quantilis ábrának is, csak a Q-Q-plot rövidebb. Lényegét tekintve ez a diagram olyan, mint egy speciális milliméterpapír, amit úgy alakítottak ki, hogy a normál eloszlás kummulatív eloszlásfüggvénye - amely egy ilyen S-alakú kígyóforma vonal – kiegyenesedjen és egy egyenesként jelenjen meg a papíron. Őszintén szólva ifjúkoromban egyszer láttam „élőben” egy ilyen nyomtatott milliméterpapírt az egyetemen, de most már annyira nincs, hogy még egy fotót is alig sikerült találnom róla a weben. Az alábbi fotó úgy körülbelül visszaadja azt, amire gondolok. A papír tetején és alján nagyok a vonalak közötti távolságok, középen viszont sűrűn vannak, így egyenesedik ki az egyébként görbe vonal.

Napjainkban már kizárólag számítógépen készít mindenki ilyen diagramokat, amelyeknek az a lényege, hogy a diagramon található egyenes vonal az elméleti kumulatív eloszlásfüggvény, az adatsor pontjait (vagy az egyes intervallumokhoz tartozó gyakoriságokat), a Q-Q plot-on ábrázolva kapunk egyfajta vizuális benyomást arról, hogy az adataink mennyire normál eloszlásúak. Értelemszerűen minél közelebb inkább ráfekszenek a pontok az egyenesre, annál inkább feltételezhetjük, hogy az adatok normál eloszlásúak.

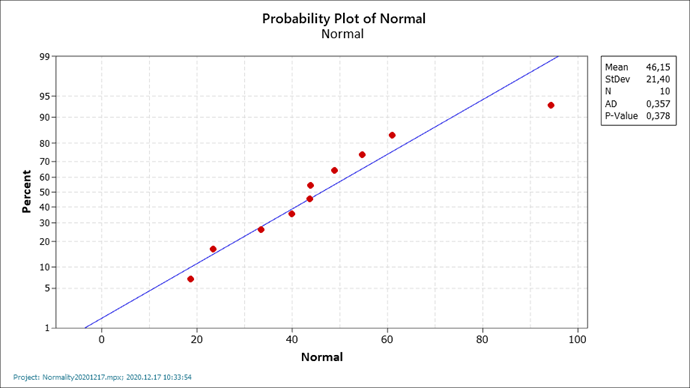
Előnye, hogy viszonylag kevés adat esetén is relatíve jól látható, hogy illeszkednek-e a pontok az egyenesre vagy sem. Önmagában – tehát valamilyen kiegészítő statisztikai próba nélkül – ez alapján sem tudunk egyértelmű döntést hozni az adatok normalitásáról, csak egyfajta „érzésünk” lehet arról, hogy mennyire jó az adatok illeszkedése.

Statisztikai próbák

Az adatok normalitását tesztelő különféle statisztikai próbákra azért van szükségünk, hogy egyértelmű döntést tudjunk hozni azzal kapcsolatban, hogy alkalmazhatók-e a normál eloszlású adatokra kidolgozott tesztek az adataink feldolgozására vagy sem. Ezek a statisztikai próbák mindegyike egyfajta illeszkedésvizsgálat, amelynek során arra vagyunk kíváncsiak, hogy a valós adatok mennyire illeszkednek arra az elméleti normál eloszlásra, amelynek a paraméterei – azaz, az átlaga és a szórása – megegyezik a valós adatok átlagával és szórásával. Hasonló illeszkedésvizsgálatról már volt szó korábban (Karl Pearson és a rulettkerék rejtélye – Khí-négyzet próba az illeszkedés vizsgálatára), a Khí-négyzet próba egy általános illeszkedésvizsgálat, ezt inkább diszkrét változók gyakorisági adatainak elemzésére használjuk. Jelen esetben viszont kifejezetten a normál eloszlásra való illeszkedést vizsgáló módszereket fogok bemutatni.

A neten több olyan cikket is lehet találni, amely arról szól, hogyan válasszunk módszert az adatok normalitásának vizsgálatára. A vélemények természetesen megoszlanak, de azért lehet találni néhány közös pontot. Itt most nem mennék bele egy teljes összefoglalóba, inkább csak szemezgetnék a leggyakrabban alkalmazott tesztek között, kiemelve ezek előnyös és hátrányos tulajdonságait.

Szinte mindegyik listán az első helyen a Kolmogorov-Smirnov teszt kerül említésre, leginkább amiatt, mert ez az egyik legegyszerűbb teszt. A teszt lényege az, hogy az adatsor átlaga és szórása alapján kiszámítjuk az elméleti normál eloszlás értékeit (vagyis, hogy mennyinek kellene lennie az adatok gyakoriságának az egyes intervallumokban, ha az adatsor tökéletesen normál eloszlású lenne), majd minden egyes intervallumban kiszámítjuk a valós adatsor és az elméleti gyakoriság közötti különbséget. Ezek közül vesszük a legnagyobbat, majd ez alapján kiszámítjuk a próba statisztikát, amelyet – a szokásos módon - összevetünk egy határértékkel. A feltevés az, hogy ez a maximális eltérés egy úgynevezett Kolmogorov-eloszlást követ, agy ha az adatsor normál eloszlású, akkor a maximális eltérés e szerint az eloszlás szerint fog változni. A határértéket táblázatból tudjuk kinézni a mintaszám és a megbízhatósági határ (95%, 99%, …) függvényében. A módszer előnye egyértelműen az egyszerűsége, hátránya viszont, hogy csak nagy mennyiségű minta esetén ad megbízható eredményt, illetve mivel a maximális eltérést vesszük figyelembe, ezért érzékeny a kieső értékekre.

A Kolmogorov-Smirnov tesztnek létezik egy módosított változata, amelynek a végrehajtása ugyanaz, mint a Kolmogorov-Smirnov-é, tehát ugyanúgy a maximális eltérést veszi alapul. Az előfeltevés viszont egy kicsit más. Amíg a Kolmogorov-Smirnov teszt esetében ismerjük a sokaság átlagát és szórását, addig a Liliefors teszt esetében nem ismerjük ezeket, így a minta átlaga és szórása alapján becsüljük ezeket. Így viszont a folyamat legvégén a döntési határértéket másképpen adjuk meg, az úgynevezett Liliefors-táblázat alapján. Ez szigorúbb határértékeket ad meg, mint a Kolmogorov-táblázat, vagyis érzékenyebb a teszt. Ennek ellenére ez a teszt is hasonlóan negatív tulajdonságokkal rendelkezik, mint a Kolmogorov-Smirnov teszt.

A következő teszt a Shapiro-Wilk teszt, amelyet kifejezetten kis mintaszám (3 – 50 minta) esetén alkalmazunk. A Shapiro-Wilk teszt alapötlete hasonló az előzőekhez, itt is az elméleti normál eloszláshoz hasonlítjuk az adatsor eloszlását, de ez esetben ez eggyel komplikáltabb, mert az elméleti gyakorisági értékeket itt másképp határozzuk meg. A próba statisztika kiszámításakor a következő folyamatot követjük:

• Az adatsor értékeit nagyság szerint növekvő sorrendbe rendezzük.
• Az így sorba rendezett adatokat párba állítjuk úgy, hogy a legnagyobb és a legkisebb lesz egy pár, az eggyel kisebb és az eggyel nagyobb lesz a következő pár, és így tovább, amíg el nem érünk a középső két értékhez (páratlan számú elem esetén a középső elem egyedül marad).
• Minden így kapott pár esetében kivonjuk a nagyobb számból a kisebbet, így megkapjuk a párok különbségeit.
• Ezeket a különbségeket megszorozzuk a Shapiro-Wilk táblázatban az adatsor mintaszámához tartozó állandókkal, amelyek az elméleti normál eloszlást reprezentálják.
• Az így kapott szorzatokat összeadjuk, így kapunk egy b értéket.
• Ezután kiszámoljuk az adatsor összes elemére az SS (Sum of Squares) értéket, amely az egyes elemek átlagtól való négyzetes eltérésének összege.
• Végül kiszámoljuk a W=b^2/SS próba statisztikát és ezt hasonlítjuk össze a másik Shapiro-Wilk táblázattal, amely a határértékeket tartalmazza.

A folyamatot értem és nem is olyan bonyolult, de azt egyelőre nem sikerült felfognom, hogy mitől működik. Ennek ellenére azt látom, hogy a módszer az adatsor összes elemét figyelembe veszi a statisztika elkészítésekor, nemcsak a maximális eltérést, így ez a teszt kevésbé érzékeny a kieső értékekre. A Minitab ennek a tesztnek egy módosított változatát használja Ryan-Joiner teszt néven.

Az utolsó ismertetett módszer az Anderson-Darling teszt. Az Anderson-Darling teszt a Kolmogorov-Smirnov tesztnek egy módosított változata, amely nagyobb súlyt ad az adatsor két végén lévő adatok illeszkedésének. Az Anderson-Darling teszt annyiban hasonlít a Shapiro-Wilk tesztre, hogy ez a teszt is figyelembe veszi az adatsor összes elemét, így valamilyen szinten egyesíti a fentebb említett tesztek pozitív tulajdonságait, plusz az előző mondatban említett extra súlyozás az adatsor szélein lévő elemek illeszkedésének. Ennél komolyabban most nem mennék bele a módszer ismertetésébe, mert a próbastatisztika meghatározásának folyamatát még le is tudnám írni, a módszer működési elvét viszont ez esetben sem értem tisztán.

Összegzés:

Az adatok normalitásának ellenőrzése fontos részét képezi a statisztikus életének és nem mindegy, hogy mikor melyik típusú tesztet alkalmazzuk ennek megállapítására. Igazából nincs kifejezetten legjobb gyakorlat, de az egyes módszerek erősségét jelző teszteken leginkább a Shapiro-Wilk és az Anderson-Darling tesztek viszik a pálmát. Igazából mindkét tesztet javaslom alkalmazni, mert amint azt fentebb leírtam, az egyik teszt inkább az adatsor szélein, míg a másik az adatsor közepén ad megbízhatóbb eredményt.

Források:

Six Sigma Material - Normality Assumption
https://www.six-sigma-material.com/Normality-Assumption.html

Real Statistics using Excel – Kolmogorov-Smirnov test for normality
https://www.real-statistics.com/tests-normality-and-symmetry/statistical-tests-normality-symmetry/kolmogorov-smirnov-test/

Real Statistics using Excel – Lilliefors Test for Normality
https://www.real-statistics.com/tests-normality-and-symmetry/statistical-tests-normality-symmetry/lilliefors-test-normality/

Real Statistics using Excel - Shapiro-Wilk Original Test
https://www.real-statistics.com/tests-normality-and-symmetry/statistical-tests-normality-symmetry/shapiro-wilk-test/

Real Statistics using Excel - One-Sample Anderson-Darling Test
https://www.real-statistics.com/non-parametric-tests/goodness-of-fit-tests/anderson-darling-test/

Nornadiah Mohd Razali, Yap Bee Wah: Power comparisons of Shapiro-Wilk, Kolmogorov-Smirnov, Lilliefors and Anderson-Darling tests, Journal of Statistical Modeling and Analytics, Vol.2 No.I, 21-33, 2011
https://www.nrc.gov/docs/ML1714/ML17143A100.pdf

The Shapiro-Wilk test for normality