1988-ban a Wall Street Journal megszervezett egy játékot, amelyet Burton Malkiel: Bolyongás a Wall Streeten című könyve ihletett, amelyben a Princeton Egyetem professzora azt merte kijelenteni, hogy egy „még egy bekötött szemű majom is, amelyik darts nyilakat dobál valamelyik gazdasági újság tőzsdei cégek listáját tartalmazó oldalaira, össze tud állítani egy legalább olyan jó portfóliót, mint a tőzsdei szakértők”. 

Amint azt már előre jeleztem, ebben a cikkben bemutatom, hogyan lehet a khí-négyzet próbát elvégezni a függetlenség vizsgálatára.

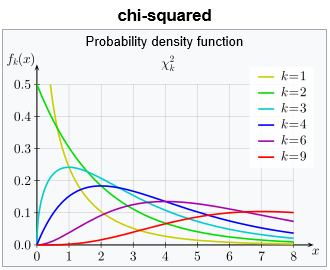
Ok, tehát nemcsak az illeszkedést lehet vizsgálni khí-négyzet próbával, hanem a függetlenséget is. Aha, de mit is jelent az, ha két jelenség független egymástól? A hétköznapi életben két jelenségről akkor mondjuk, hogy függetlenek egymástól, ha azok nem befolyásolják egymást. Ha az egyik jelenséghez tartozik egy A esemény, a másik jelenséghez pedig egy B esemény, akkor a két eseményt akkor nevezzük egymástól független eseményeknek, ha az A esemény eredményét nem befolyásolja a B esemény eredménye és fordítva, a B esemény eredményét sem befolyásolja az A esemény eredménye. Matematikusok ezt úgy szokták megfogalmazni, hogy ha az A és a B események függetlenek egymástól, akkor az A és a B események együttes bekövetkezésének a valószínűsége megegyezik az A esemény és a B esemény külön-külön vett bekövetkezési valószínűségének a szorzatával.

Az előző cikkben (Karl Pearson és a rulettkerék rejtélye – Khí-négyzet próba az illeszkedés vizsgálatára) levezettem a khí-négyzet próbát az illeszkedés vizsgálatára felhasználva Karl Pearson eredeti adatait a rulett sorozatok és az érmefeldobás sorozatok vizsgálatára. Mivel mindig érdekes az, hogy egy statisztikai szoftver hogyan dolgozza fel az adatokat, illetve hogyan tálalja elénk a tesztek eredményeit, most is szeretném nektek lépésről lépésre bemutatni, hogy hogyan készíteném el ezt az elemzést a Minitab statisztikai elemző programmal.

Egy korábbi bejegyzésben már bemutattam (Roulette a la Monte Carlo, avagy csaltak vagy nem csaltak...?), hogy Karl Pearson matematikus az 1890-es években sokat foglalkozott a rulettel és azzal, hogy vajon a monacói kaszinók rulettkerekei mennyire működnek véletlenszerűen. Úgy döntöttem, hogy megvizsgálom egy kicsit részletesebben, hogy mi is volt a híres matematikus problémája és egyben megragadom az alkalmat az illeszkedés vizsgálatára alkalmazott khí-négyzet próba bemutatására.

Mielőtt tovább mennénk a különféle statisztikai tesztek dzsungelében, sajnos nem ússzuk meg egy-két további eloszlás típussal (sajnos lesz még egy pár). A következő eloszlás típus, amiről szót kell ejtenünk az úgynevezett Khí-négyzet eloszlás.

Ott tartottunk, hogy összehasonlítottuk két egymástól független minta átlagát, vajon megegyeznek-e (Az alkoholfogyasztás hatása a bowling eredményekre – kétmintás t-próba). Noha még itt is lehetne elmélkedni egy csomó dologról, például arról, hogy másképpen számoljuk ki ’t’ értékét, ha feltételezzük, hogy a két minta szórása megegyezik, vagy hogy miért számolja a Minitab a szabadsági fokok számát azzal a bonyolult képlettel (Kétmintás t-próba táblázatkezelőben), de most inkább hagyjuk Samut pihenni a sok bowlingozás után.

Miután ilyen szerencsésen megismerkedtünk a kétmintás t-próbával (Az alkoholfogyasztás hatása a bowling eredményekre – kétmintás t-próba), tehát az eddigi gyakorlatnak megfelelően vezessük le táblázatkezelőben és Minitab-ban is az előző cikkben említett feladatot.

Az egymintás t-próba esetében (Z helyett t – leheletnyi különbség) még mindig volt egy sokaságunk, noha nem ismertük a szórását. Akkor most elimináljuk a kiinduló feltételek közül a sokaság utolsó írmagját is, azaz a sokaság átlagát. Így elérjük azt az állapotot, amikor már semmit sem tudunk a sokaságról. Rendben, de akkor mihez fogjuk hasonlítani a kis mintánkat?

Egy előző cikkben (Számítógépes bowlingozás egymintás Z-próbával) már bemutattam, hogy hogyan lehet táblázatkezelő segítségével elvégezni az egymintás Z-próbát. Most már könnyebb dolgom van, hiszen csak néhány apróságot kell átalakítanom az előzőleg elkészült táblázatban ahhoz, hogy megkapjam az egymintás t-próbát elvégezni képes táblázatot.